12.4: Digital-Analog-Wandlungstechniken
Der grundlegende Digital-Analog-Wandler ist wenig mehr als ein gewichteter Summierverstärker. Jedes aufeinanderfolgende Bit im digitalen Wort repräsentiert einen Pegel, der doppelt so groß ist wie der des vorangegangenen Bits. Wenn jedes Bit als ein bestimmter Strom oder eine bestimmte Spannung aufgefasst wird, können die ansteigenden Pegel durch Verwendung unterschiedlicher Verstärkungen in den Summierungseingängen erzeugt werden. Ein einfacher 4-Bit-Wandler ist in Abbildung \(\PageIndex{1}\) dargestellt.
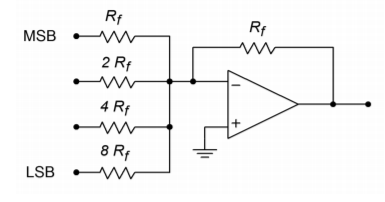
Abbildung \(\PageIndex{1}\): Ein einfacher 4-Bit-Wandler.
Dieses System kann \(2^4\), also 16, verschiedene Pegel darstellen. Jeder Eingang wird durch einen einfachen High/Low-Logikpegel angesteuert, der eine 1 oder 0 für das jeweilige Bit darstellt. Beachten Sie, dass die Eingangswiderstände um den Faktor 2 variieren. Die Verstärkung für den obersten Pfad ist \(R_f/R_f\), also Eins. Dieser Eingang wird für das höchstwertige Bit des Eingangsworts (MSB) verwendet. Der nächste Eingang zeigt eine Verstärkung von \(R_f / (2R_f)\), also 0,5. Der dritte Eingang weist eine Verstärkung von 0,25 auf, und der letzte Eingang weist eine Verstärkung von 0,125 auf. Der letzte Eingang hat die geringste Verstärkung und wird für das niederwertigste Bit des Eingangswortes (LSB) verwendet. Hätte das Eingangswort eine höhere Auflösung (d. h. mehr Bits), würden zusätzliche Kanäle hinzugefügt, die jeweils die halbe Verstärkung des vorhergehenden Eingangs aufweisen. Um den Konvertierungsprozess besser zu verstehen, lassen Sie uns einen Blick auf einige repräsentative Ein- und Ausgänge werfen.
Die Schaltung aus Abbildung \(\PageIndex{1}\) kann mit einfachen 5 V TTL-Logikschaltungen betrieben werden. 5 V stellt ein logisches High dar, während 0 V ein logisches Low darstellt. Wie hoch ist der Ausgangspegel, wenn das Eingangswort 0100 ist? Da ein logisches High 5 V repräsentiert, werden 5 V an den zweiten Eingang angelegt. Alle anderen Eingänge erhalten ein logisches Low, also 0 V. Der Ausgang ist die Summe der Eingangssignale (denken Sie daran, dass es sich um einen invertierenden Summierer handelt, also sollte der endgültige Ausgang das umgekehrte Vorzeichen haben).
\
Ein Wert von 4 (binär 100) entspricht also einem Potential von 2,5 V. Wenn wir den Wortwert auf 9 (binär 1001) erhöhen, sehen wir
Das Minimum des Ausgangs tritt bei binär 0000 auf, (0 V) und das Maximum bei binär 1111 (-9,375 V). Die Schrittweite ist gleich dem Logikpegel mal der minimalen Verstärkung; in diesem Fall sind das 0,625 V. Beachten Sie, dass der Ausgangswert durch einfache Multiplikation des Wertes des Eingangswortes mit der minimalen Schrittweite ermittelt werden kann. Außerdem ist es wichtig zu beachten, dass das Ausgangssignal unipolar ist (in diesem Beispiel immer negativ).
Eine digitale Darstellung besteht natürlich aus einer Folge von Worten, nicht nur aus einem Wort. In der Realität füttern die Logikschaltungen den Summierverstärker ständig mit neuen Wörtern in einer vorgegebenen Rate. Durch die wechselnden Eingänge ändert sich auch der Ausgang des Wandlers ständig. Unter Verwendung unserer zuvor berechneten Werte, wenn der Konverter mit der Sequenz \(0000, 0100, 1001, 1111,\) gefüttert wird, bewegt sich der Ausgang von 0 V zu -2,5 V, zu -5.625 V, bis zu einem Endwert von -9,375 V. Dieser Ausgang ist in Abbildung \(\PageIndex{2}\) grafisch dargestellt.
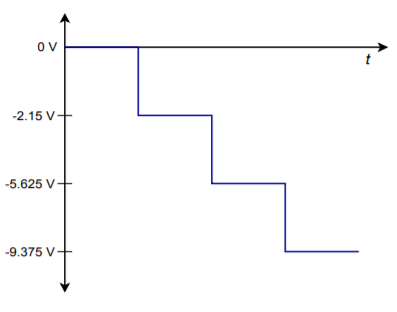
Abbildung \(\PageIndex{2}\): Ausgabe mit vier digitalen Worten.
Wenn diese Sequenz immer wieder wiederholt wird, ergibt sich die Wellenform von Abbildung \(\PageIndex{3}\). Beachten Sie, dass eine Welle vom Typ „Treppe“ erzeugt wird. Sie können sich dies auch als eine sehr grobe Form einer Rampenfunktion vorstellen. Eine bessere Rampe würde erzeugt werden, wenn wir alle verfügbaren Werte für die Eingangssequenz verwenden würden, wie in \(0000, 0001, 0010, 0011, \dots , 1111\). Um den negativen DC-Offset zu entfernen und das Signal bipolar zu machen, müssen wir das Signal nur noch durch einen Koppelkondensator leiten. Die Frequenz dieser Wellenform wird durch die Rate gesteuert, mit der die Worte dem Wandler zugeführt werden. Beachten Sie, dass durch Erhöhung der Auflösung und der Anzahl der Worte, die dem Wandler pro Zyklus zugeführt werden, eine sehr gute Annäherung an die ideale Rampenfunktion erreicht werden kann. Indem man die Eingangsworte in andere Sequenzen ändert, kann man eine große Vielfalt von Ausgangswellenformen erzeugen. Dies ist das Konzept hinter dem digitalen Arbiträrfunktionsgenerator. Ein Arbiträrfunktionsgenerator erlaubt es Ihnen, Wellenformen zu erzeugen, die über die einfachen Sinus-, Rechteck- und Dreieckskurven hinausgehen, die man bei einem typischen Labor-Funktionsgenerator findet. Wir werden uns dieses spezielle Testgerät etwas später genauer ansehen.
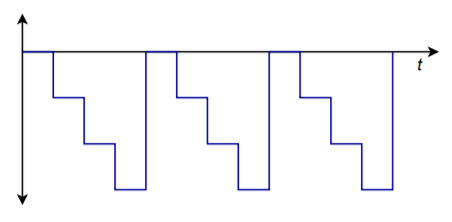
Abbildung: Getaktete Ausgabe.
Um die Auflösung zu erhöhen, scheint es, dass man am Summierverstärker nur zusätzliche Kanäle mit immer größeren Widerständen hinzufügen muss. Leider werden die Widerstandsgrößen bald unpraktisch und ein anderer Ansatz ist erforderlich. Zum Beispiel würde ein 16-Bit-System erfordern, dass der LSB-Widerstand gleich 65.536 \(R_f\) ist. Ein Problem ist, dass der daraus resultierende kleine Eingangsstrom durch Eingangsvorspannungs- und Offsetströme in den Schatten gestellt werden kann. Außerdem ist eine hohe Bauteilgenauigkeit für die wichtigeren Eingänge in Bezug auf die Eingangswiderstände und die Treibersignale erforderlich. Die übermäßig großen Widerstände können auch zu zusätzlichem Rauschen beitragen. Die Standardlösung für dieses Problem besteht in der Verwendung eines \(R/2R\)-Widerstandsteilernetzwerks.
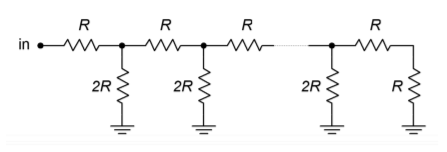
Abbildung \(\PageIndex{4}\): \Ein Leiternetzwerk
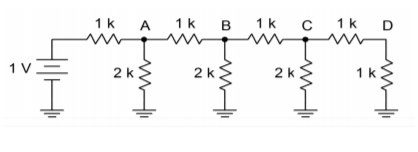
Abbildung \(\PageIndex{5}\): Eine 4-stufige Leiter.
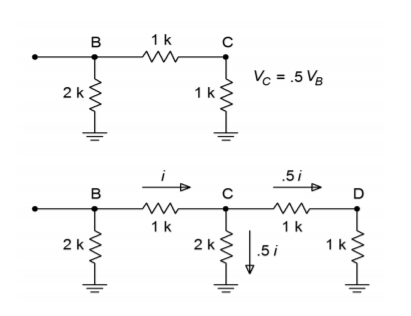
Abbildung \(\PageIndex{6}\): Ladder-Analyse. a. Ersatzschaltbild (oben). b. Stromaufteilung (unten).
Wenn Sie sich den Ersatzschaltbild-Abschnitt von Abbildung \(\PageIndex{6}\) ansehen, werden Sie feststellen, dass dieser Abschnitt nun genau wie der letzte Abschnitt des ursprünglichen Netzwerks aussieht. Das heißt, jedes Mal, wenn ein Abschnitt vereinfacht und analysiert wird, ist das Ergebnis eine Halbierung von Spannung und Strom. Es ist bereits offensichtlich, dass die Spannung an \(D\) die Hälfte der Spannung an \(C\) sein muss, die wiederum die Hälfte der Spannung an \(B\) sein muss. Wie Sie nun beweisen können, folgt daraus, dass die Spannung an \(B\) die Hälfte der Spannung an \(A\) sein muss. In ähnlicher Weise ist der Strom, der durch jedes \(2R\)-Schenkel fließt, die Hälfte des vorhergehenden Stroms. (Bei der Stromteilung wird der letzte Abschnitt nicht zur Ableitung eines Stroms verwendet, da er gleich dem Wert in der vorhergehenden Stufe ist.) Die Halbierung des Stroms ist genau das, was für die binäre Darstellung des digitalen Eingangsworts benötigt wird.
Die Anpassung des \(R/2R\)-Netzwerks an den DA-Wandler ist relativ einfach. Das Netzwerk wird von einer stabilen Stromquelle gespeist, wobei jedes \(2R\)-Element in einen Summierverstärker einspeist. In Reihe mit jedem \(2R\)-Element befindet sich ein Halbleiterschalter, der den entsprechenden Logikpegel einstellt. Dies ist in Abbildung \(\PageIndex{7}\) dargestellt, wobei das Netzwerk effektiv auf der Seite liegt. Wenn ein logischer High-Pegel an ein bestimmtes Bit angelegt wird, wird der Schalter geschlossen und Strom fließt durch das \(2R\)-Element und in den Operationsverstärker. Beachten Sie, dass das rechte Ende des Widerstands effektiv auf Masse liegt, da der Summenknoten des Operationsverstärkers eine virtuelle Masse ist. Wenn ein logischer Low-Wert anliegt, leitet der Schalter den Strom zur Masse und überbrückt den Operationsverstärker. Auf diese Weise werden die entsprechend gewichteten Ströme summiert und zur Erzeugung der Ausgangsspannung verwendet.
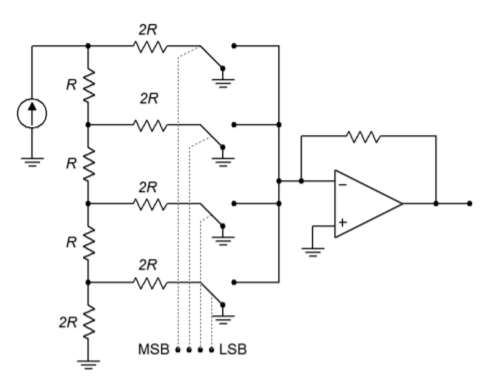
Abbildung \(\PageIndex{7}\): Wandler mit R/2R-Leiter.
Dieses Verfahren bietet mehrere Vorteile gegenüber der einfacheren Version mit gewichteter Verstärkung. Erstens werden alle Zweige von einer gemeinsamen Stromquelle gespeist. Dadurch entfällt die Notwendigkeit einer Ausgangspegelanpassung. Zweitens sind nur zwei verschiedene Widerstandswerte für eine beliebige Anzahl von Bits erforderlich, anstatt des unpraktisch großen Bereichs, der früher verwendet wurde. Es ist wirtschaftlicher, die Toleranz von nur zwei verschiedenen Teilen zu kontrollieren als 12 oder 16. Beachten Sie, dass für die niederwertigsten Bits immer noch kleine Eingangsströme erzeugt werden, so dass die Beachtung der Eingangsvorspannung und der Offsetströme wichtig bleibt.
12.4.1: Praktische Grenzen des Digital-Analog-Wandlers
Die vielleicht offensichtlichste Grenze, die mit dem DA-Wandler verbunden ist, ist seine Geschwindigkeit. Der im DAC verwendete Operationsverstärker muss viel schneller sein als die Endsignale, die er erzeugen soll. Eine bestimmte Ausgangswellenform kann mehrere Dutzend einzelne Abtastpunkte pro Zyklus enthalten. Der Operationsverstärker muss auf jeden Abtastpunkt reagieren. Folglich sind eine große Bandbreite und hohe Anstiegsgeschwindigkeiten erforderlich.
Integrierte DAC-Datenblätter bieten ein paar wichtige Parameter, die Sie kennen sollten. Da ist zunächst einmal die Wandlungsgeschwindigkeit. Diese Zahl gibt an, wie lange der DAC braucht, um das digitale Eingangswort in eine stabile analoge Ausgangsspannung zu verwandeln. Damit wird die maximale Datenrate festgelegt. Als nächstes kommen die Genauigkeit und die Auflösung. Die Auflösung gibt die Anzahl der diskreten Schritte an, die am Ausgang erzeugt werden können, und wird durch die Anzahl der verfügbaren Bits festgelegt. Dies ist nicht dasselbe wie die Genauigkeit. Die Genauigkeit setzt sich aus verschiedenen Faktoren zusammen, darunter Offset-Fehler, Fehler und Nichtlinearität. Der Offset-Fehler wird normalerweise gemessen, indem ein Eingangswort mit dem Wert Null angelegt und dann das Ausgangssignal gemessen wird. Im Idealfall beträgt dieses Signal Null Volt. Die Abweichung von Null wird als der Offset-Fehler genommen. Dies hat den Effekt, dass alle Ausgangspegel um eine konstante Spannung ungenau werden. Der Offset-Fehler ist in vielen Anwendungen relativ einfach zu kompensieren, indem ein gleicher Offset mit entgegengesetzter Polarität angelegt wird. Der Gain-Fehler ist eine Abweichung, die jeden Ausgangspegel um einen konstanten Prozentsatz beeinflusst. Es ist, als ob das Signal durch einen kleinen Verstärker oder ein Dämpfungsglied geleitet würde. Dieser Fehler kann kompensiert werden, indem ein Verstärker mit einer Verstärkung verwendet wird, die dem Kehrwert des Fehlers entspricht. Die beiden Verstärkungen heben sich effektiv auf. Die Auswirkungen von Offset- und Verstärkungsfehler sind in den Abbildungen \(\PageIndex{8}\) und \(\PageIndex{9}\) dargestellt.
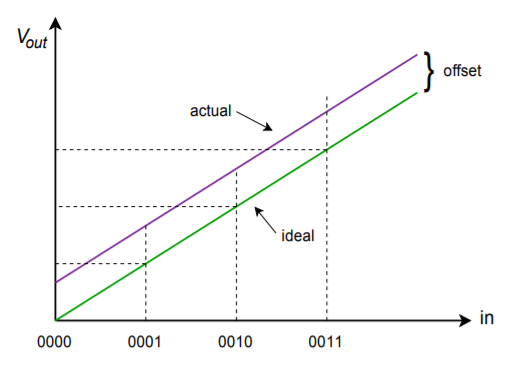
Abbildung \(\PageIndex{8}\): Nur Offset-Fehler.
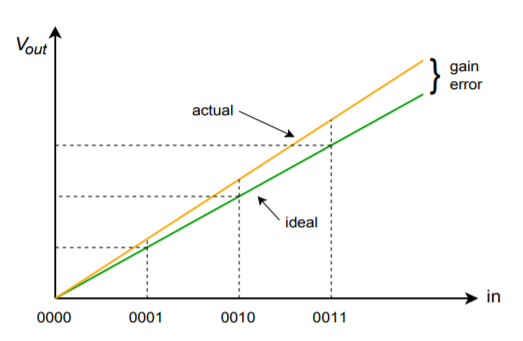
Abbildung \(\PageIndex{9}\): Nur Verstärkungsfehler.
Nichtlinearitätsfehler können in zwei Formen unterteilt werden: integrale Nichtlinearität und differentielle Nichtlinearität. Die integrale Nichtlinearität gibt den maximalen Versatz zwischen den idealen Ausgängen und den tatsächlichen Ausgängen für alle möglichen Eingänge an. Die differentielle Nichtlinearität gibt die maximale Ausgangsabweichung relativ zu einem LSB an, die durch zwei benachbarte Eingangsworte verursacht wird. Wenn die differentielle Nichtlinearität über \(\pm 1\) LSB liegt, kann das System nicht monoton sein. Mit anderen Worten: Ein höheres digitales Eingangswort kann tatsächlich eine niedrigere analoge Ausgangsspannung erzeugen. Diese beiden Formen des Fehlers sind in Abbildung \(\PageIndex{10}\) dargestellt. Beachten Sie, dass es möglich ist, eine hohe integrale Nichtlinearität und dennoch eine geringe differentielle Nichtlinearität zu haben. Dies ist der Fall in Abbildung \(\PageIndex{10b}\).
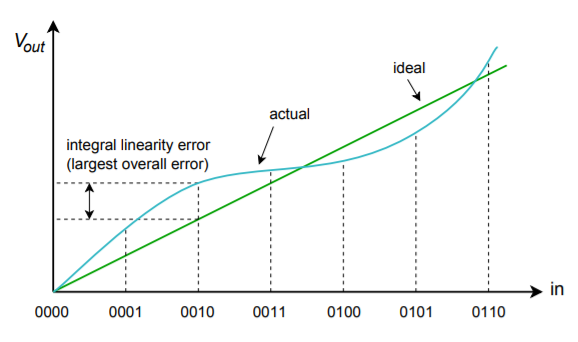
Abbildung \(\PageIndex{10a}\): Linearitätsfehler Integraler Linearitätsfehler.
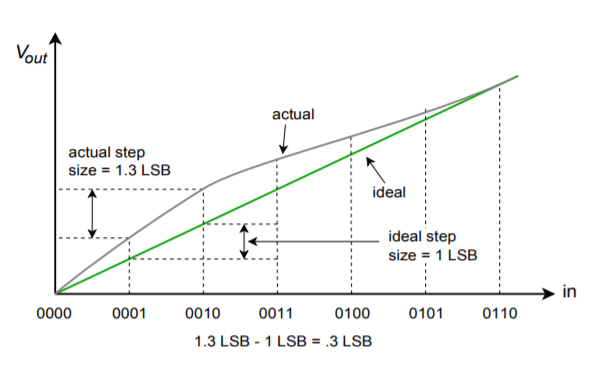
Abbildung \(\PageIndex{10b}\): Linearitätsfehler (Fortsetzung) Differential-Linearitätsfehler (Relativ-Adjacent Error).
Wie Sie sehen, ist die Genauigkeit von ziemlich komplexen Faktoren abhängig. In dem Bemühen, dies auf eine einzige Zahl herunterzubrechen, geben einige Hersteller eine effektive Anzahl von Bits an. Zum Beispiel kann ein 16-Bit-DAC mit einer Genauigkeit von 14 Bit angegeben werden. Das bedeutet, dass die 14 höchstwertigen Bits sich idealisiert verhalten, aber die untersten 2 Bits können durch Linearitätsfehler überdeckt werden. Eine weitere Spezifikation, die Sie manchmal sehen, ist „no missing codes“. Das bedeutet, dass für jede Erhöhung des Eingangsworts eine entsprechende positive Ausgangspegeländerung erfolgt.
In der Praxis wird der Standard-DA-Wandler mit einem Ausgangsfilter verwendet. Wie Sie in den vorherigen Abbildungen sehen können, enthalten die vom DAC erzeugten Wellenformen einen Treppeneffekt. Dies ist im Allgemeinen nicht erwünscht. Die abrupten Änderungen des Ausgangspegels deuten darauf hin, dass höhere Frequenzkomponenten vorhanden sind. Alle Komponenten oberhalb der Nyquist-Rate sollten mit einem geeigneten Tiefpassfilter herausgefiltert werden. Dieser Filter wird manchmal auch als Rekonstruktions- oder Glättungsfilter bezeichnet. In einem unsachgemäß ausgelegten System entfernt der Rekonstruktionsfilter einige der höchsten In-Band-Frequenzkomponenten (d. h. Komponenten unmittelbar unterhalb der Nyquist-Frequenz). Um dies zu kompensieren, werden die Logikpegel oft für verkürzte Zeiträume an den DAC angekoppelt, wodurch ein eher spitzes Erscheinungsbild als die Treppenform entsteht. Dieser Effekt ist in Abbildung \(\PageIndex{11}\) dargestellt. Obwohl diese spitze Wellenform weniger wünschenswert erscheint als die Treppenform, erzeugt sie höhere Pegel für die obersten Komponenten, und nach der Filterung ist das Ergebnis ein glatterer Gesamtfrequenzgang.
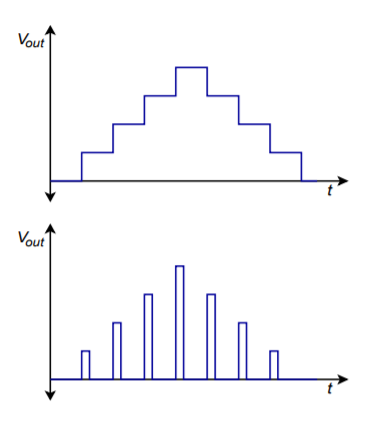
Abbildung \(\PageIndex{11}\): Ausgangsrekonstruktion. a. Vollperioden-Latch (oben). b. Teilperioden-Latch (unten).
Um die Qualität der Ausgangswellenform weiter zu erhöhen, wird manchmal eine Technik verwendet, die als Oversampling bekannt ist. Die Grundidee besteht darin, neue Abtastpunkte zwischen den vorhandenen zu erzeugen. Das Ergebnis ist eine viel dichtere Datenrate, die nach der Filterung hoffentlich genauere Ergebnisse liefert. Außerdem kann die höhere Datenrate die Anforderungen an den Rekonstruktionsfilter lockern. Ein typisches System könnte ein vierfaches Oversampling verwenden, was bedeutet, dass die Ausgangsdatenrate das Vierfache des Originals beträgt. Daher müssen für jedes Eingangswort drei neue Wörter hinzugefügt werden. Dieser Effekt ist in Abbildung \(\PageIndex{12}\) dargestellt.
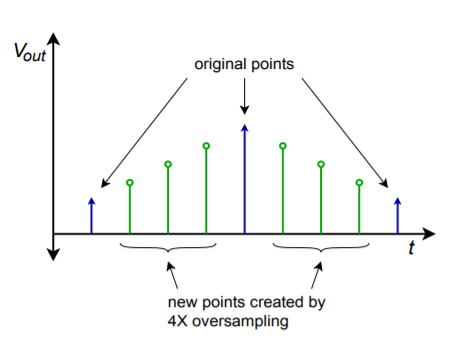
Abbildung \(\PageIndex{12}\): Überabgetastete Ausgabe.
Es gibt eine Reihe von Möglichkeiten, die neuen Abtastpunkte zu erzeugen. Der naheliegendste Weg ist eine einfache Interpolation, die aber nicht die besten Ergebnisse erzielt. Eine andere Technik besteht darin, die neuen Werte auf Null zu initialisieren und dann den Datenstrom durch einen digitalen Tiefpassfilter zu leiten, der effektiv die richtigen Werte berechnet. Eine Erweiterung des Oversampling-Prinzips ist die Delta-Sigma-Technik. Bei der Delta-Sigma-Technik werden sehr hohe Oversampling-Raten in Verbindung mit speziellen digitalen Filteralgorithmen verwendet. Die Algorithmen tauschen im Wesentlichen die höhere Datenrate gegen eine langsamere Rate mit erhöhter Auflösung. Das Design und die Analyse von Delta-Sigma-Systemen ist ziemlich fortgeschritten und würde den Rahmen dieses Textes sprengen. Es genügt zu sagen, dass diese Techniken die Qualität des Ausgangssignals erhöhen können und in Anwendungen wie hochwertigen Audio-CD- und DVD-Playern weit verbreitet sind.
12.4.2: Integrierte Schaltungen für Digital-Analog-Wandler
Es gibt viele mögliche Anwendungen für Digital-Analog-Wandler, und eine Reihe von verschiedenen Chips hat sich entwickelt, um spezifische Anforderungen zu erfüllen. Im Allgemeinen kann man diese in bestimmte Klassen einteilen, wie z.B. hohe Geschwindigkeit, hohe Auflösung oder geringe Kosten. Wir werden drei repräsentative Typen untersuchen. Die Geräte, die wir uns ansehen werden, sind der DAC0832, ein einfacher 8-Bit-Wandler, der DAC7545, ein mikroprozessorkompatibler 12-Bit-Wandler, und der PCM1716, ein hochwertiger 24-Bit-Wandler, der in der Audioindustrie verwendet wird.
DAC0832
Dieser IC ist ein beliebter mikroprozessorkompatibler 8-Bit-Wandler. Der DAC0830 und der DAC0831 sind ähnlich, jedoch mit etwas reduzierter Leistung. Es handelt sich um einen multiplizierenden DAC. Mit anderen Worten, das Ausgangssignal ist eine Funktion des digitalen Eingangswortes und eines Referenzeingangs. In einigen Anwendungen ist der Referenzeingang nicht fest, sondern ein variables Eingangssignal. Eine Funktionsliste und Pinbelegung ist in Abbildung \(\PageIndex{13}\) dargestellt. Hervorzuheben sind die Einschwingzeit von nur 1 \(\mu\) s, der geringe Leistungsbedarf und die hohe Linearität. Der DAC0832 kann entweder im Stand-alone-Modus oder mit einem Mikroprozessor verwendet werden. Die Schaltwellenformen sind in Abbildung \(\PageIndex{14}\) dargestellt.

Abbildung \(\PageIndex{13}\): DAC0832. Nachdruck mit freundlicher Genehmigung von Texas Instrutment

Abbildung \(\PageIndex{14}\): DAC0832-Schaltwellenformen Abgedruckt mit freundlicher Genehmigung von Texas Instrutments
Eine interessante Anwendung des DAC0832 ist in Abbildung \(\PageIndex{15}\) zu sehen. Im Grunde handelt es sich um ein digital gesteuertes Zustandsvariablenfilter.
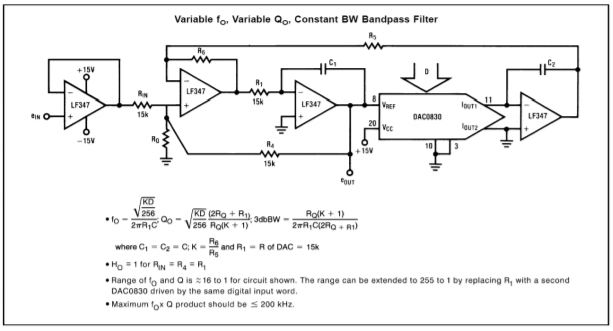
Abbildung \(\PageIndex{15}\): Anwendung des Zustandsvariablenfilters DAC0832. Nachdruck mit freundlicher Genehmigung von Texas Instrutments
Beachten Sie, dass der Wandler den Eingangswiderstand des zweiten Integrators ersetzt. Normalerweise würde dieser Widerstand verwendet werden, um die Ausgangsspannung des ersten Integrators in einen Eingangsstrom für den zweiten Integrator zu wandeln. Diese Aufgabe wird nun vom DAC0832 übernommen. Das digitale Eingangswort legt effektiv die Spannungs-Strom-Wandlung fest. Somit verändert eine Änderung des Eingangswortes die Abstimmfrequenz des Filters wie ein Potentiometer. Vergleichen Sie diese Schaltung mit dem spannungsgesteuerten Filter auf OTA-Basis aus Kapitel 11. Konzeptionell sind sie sich sehr ähnlich.

Abbildung: DAC7821. Nachdruck mit freundlicher Genehmigung von Texas Instruments
DAC7821
Der DAC7821 ist ein ziemlich standardmäßiger 12-Bit-Linearwandler und ist in Abbildung \(\PageIndex{16}\) dargestellt. Seine interessanten Aspekte sind, dass er ein multiplizierender Wandler ist und dass er mikroprozessorkompatibel ist. Der Multiplikationseffekt ergibt sich aus der Tatsache, dass eine Referenz verwendet wird, um das \(R/2R\)-Kettennetzwerk zu steuern. Wenn die Referenz geändert wird, wird der Ausgang effektiv neu skaliert. Folglich können Sie sich das Ausgangssignal als gleich dem Referenzwert mal dem digitalen Eingangswort vorstellen. Man kann sich dies auch als eine Art „digitale Lautstärkeregelung“ vorstellen.
Durch die Aufnahme einiger zusätzlicher Logikleitungen ist der IC mikroprozessorkompatibel geworden. Das bedeutet, dass der DAC7821 neben den 12 Dateneingangsleitungen auch Chip-Select- und Read/Write-Leitungen besitzt. Dadurch kann der Wandler direkt an den Datenbus des Mikroprozessors angeschlossen werden. Durch die Verwendung von Memory-mapped I/O kann der Mikroprozessor Daten in den Wandler schreiben, genauso wie er Daten in den Speicher schreibt. Ein 16-Bit-Mikroprozessorsystem kann dem Wandler alle benötigten Daten in einem Schreibzyklus zur Verfügung stellen, ein 8-Bit-Mikroprozessor benötigt jedoch zwei Schreibzyklen und eine Art von Latch. Eine Adresse kann für die unteren 8 Bits und eine weitere Adresse für die restlichen 4 Bits verwendet werden. Ein vereinfachtes System ist in Abbildung \(\PageIndex{17}\) unter Verwendung eines 8-Bit-Mikroprozessors dargestellt.
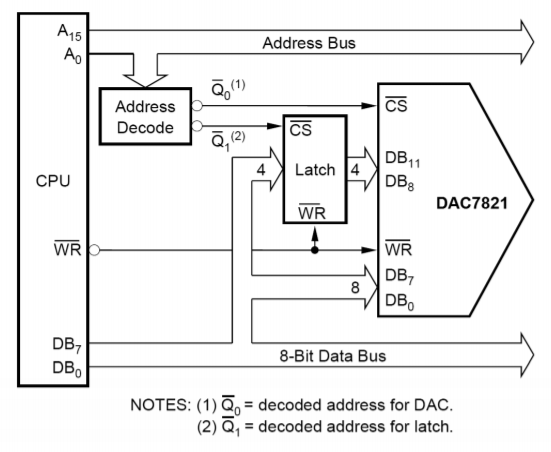
Abbildung \(\PageIndex{17}\): Schnittstelle zwischen Mikroprozessor und DAC7821. Nachdruck mit freundlicher Genehmigung von Texas Instruments
PCM5242
Der PCM5242 ist ein Stereo-24-Bit-Wandler, der speziell für hochwertige digitale Audioanwendungen entwickelt wurde. Er wird in einem VQFN-Gehäuse (Very thin Quad Flat No-lead) geliefert. Ein Blockdiagramm und eine Funktionsliste sind in Abbildung \(\PageIndex{18a}\) dargestellt. Im Gegensatz zu den anderen Konvertern verfügt der PCM5242 über einen seriellen und nicht über einen parallelen Dateneingang. Er verfügt über eine eigene On-Board-Serienwandlerschaltung und -logik. Diese Technik hilft, die Systemkosten zu reduzieren. Es ist auch überraschend praktisch, da viele spezialisierte digitale Signalverarbeitungs-ICs, die mit dem PCM5242 verwendet werden könnten, einen seriellen Ausgang verwenden. Dieser kann direkt in das PCM5242 im 16-, 24- oder 32-Bit-Format eingespeist werden.

Abbildung: PCM5242. Nachdruck mit freundlicher Genehmigung von Texas Instruments
Das Spezifikationsblatt des PCM5242 ist in Abbildung \(\PageIndex{18b}\) dargestellt. Beachten Sie, dass dieses Gerät mit Abtastraten von 48 kHz bis 192 kHz spezifiziert ist. Die gesamte harmonische Verzerrung plus Rauschen liegt typischerweise 94 dB unter einem Vollausschlag, wenn es mit einer dieser Abtastraten verwendet wird. Aufgrund der hohen Auflösung und des Dynamikbereichs von 114 dB muss beim Schaltungslayout besonders sorgfältig vorgegangen werden, um Brummeinstreuungen und HF-Störungen zu vermeiden.
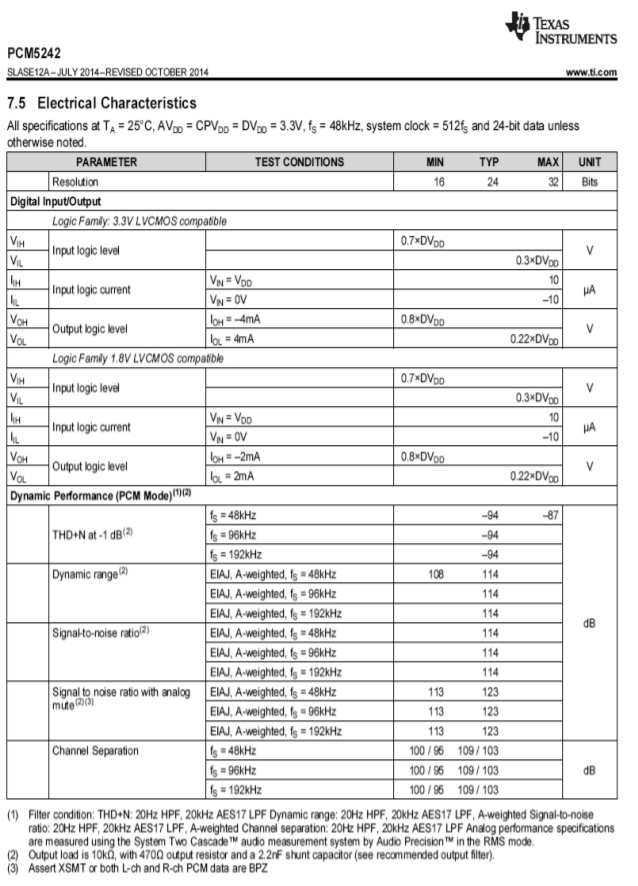
Abbildung: PCM5242-Spezifikationen. Nachdruck mit freundlicher Genehmigung von Texas Instruments
12.4.3: Anwendungen von integrierten Digital-Analog-Wandler-Schaltungen
Beispiel \(\PageIndex{1}\)
Vielleicht ist das erste, woran viele Menschen denken, wenn sie die Begriffe digital oder digitalisiert hören, die Audio-Compact-Disk, kurz CD. Der CD-Player für den Heimgebrauch ist ein hervorragendes Beispiel für den Einsatz von präzisen DA-Schaltungen in unserem Alltag. Musikdaten werden auf der CD mit 16 Bit Auflösung und einer Abtastrate von 44,1 kHz gespeichert. Dies ergibt eine Nyquist-Frequenz von 22,05 kHz, die hoch genug ist, um den Hörbereich der meisten Menschen zu umfassen. Fehlerkorrektur- und Hilfsdaten sind ebenfalls auf der Platte gespeichert. Die Daten werden auf der Platte in Form von sehr kleinen Pits gespeichert, die von einem Laser gelesen werden. Das Signal wird dann in die übliche elektronische Logikform umgewandelt, wo es auf Fehler geprüft und gegebenenfalls angepasst wird. Der Datenstrom wird dann dem DA-Wandler zur Audiorekonstruktion zugeführt. Ein einzelner Wandler kann zwischen den beiden Stereokanälen gemultiplext werden, oder es können zwei dedizierte Wandler verwendet werden. Zur Verbesserung der Signalqualität wird häufig ein Oversampling im Bereich von 2X bis 8X verwendet. Ein Blockdiagramm des Systems ist in Abbildung \(\PageIndex{19}\) dargestellt. Der eigentliche DAC-Teil erscheint im Vergleich zu einigen der anspruchsvolleren Elemente fast trivial.
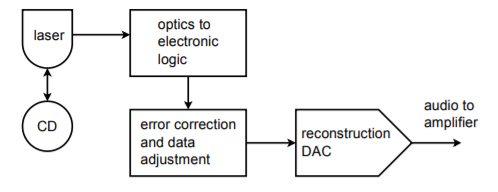
Abbildung \(\PageIndex{19}\): Audio-Compact-Disk-Wiedergabesystem.
Die Speicherdichte der optischen CD ist beachtlich. Diese kleine Scheibe (weniger als 5 Zoll im Durchmesser) kann 70 Minuten Musik speichern. Ignorieren wir die Zusatzdaten, können wir schnell den Gesamtspeicher berechnen. Wir haben zwei Kanäle mit 16-Bit-Daten oder 32 Bit (4 Byte) pro Abtastpunkt. Es gibt 44.100 Samples pro Sekunde für 70 Minuten, was 185,22 Megasamples ergibt. Der gesamte Datenspeicher beträgt 5,927 Gigabit, also 741 Megabyte.
Beispiel \(\PageIndex{2}\)
Wie bereits erwähnt, ist es möglich, DACs direkt an Mikroprozessorsysteme anzuschließen. Außerdem kann der Mikroprozessor in den DAC schreiben, ohne mehr Aufwand als beim Schreiben in einen Speicherplatz. Der Mikroprozessor kann jede beliebige Folge von Datenwörtern in den DAC schreiben und kann eine Sequenz praktisch ewig wiederholen. Mit dieser Fähigkeit können wir einen Generator für eine beliebige Wellenform bauen. Anstatt auf eine Reihe von vordefinierten Wellenformen festgelegt zu sein, wie es bei gewöhnlichen Funktionsgeneratoren der Fall ist, erlaubt dieses System alle Arten von Wellenformen. Die Genauigkeit und Flexibilität des Systems hängt von seiner Geschwindigkeit und der verfügbaren DAC-Auflösung ab.
Die Grundidee ist die eines Tabellen-Look-ups. Nehmen wir zum Beispiel an, dass wir ein 16-Bit-System haben. Wir werden eine Tabelle mit Datenwerten für einen Zyklus der Ausgangswellenform erstellen. Der Einfachheit halber können wir die Tabellengröße als praktische Potenz von 2, z. B. 256, festlegen. Mit anderen Worten, ein einzelner Ausgangszyklus wird in 256 diskrete Zeitabschnitte zerlegt. Es ist also offensichtlich, dass der Wandler einige hundert Mal schneller sein muss als die höchste Grundschwingung, die wir erzeugen wollen. Durch Erhöhen oder Verringern der Ausgangsdatenrate können wir die Frequenz der Ausgangsgrundschwingung ändern. Dies wird als Technik der variablen Abtastrate bezeichnet. Es ist auch möglich, die Grundfrequenz mit einer Technik mit fester Abtastrate zu ändern (dies ist etwas komplexer, bietet aber gewisse Vorteile). Ein Ausgangsablaufplan ist in Abbildung \(\PageIndex{20}\) dargestellt.
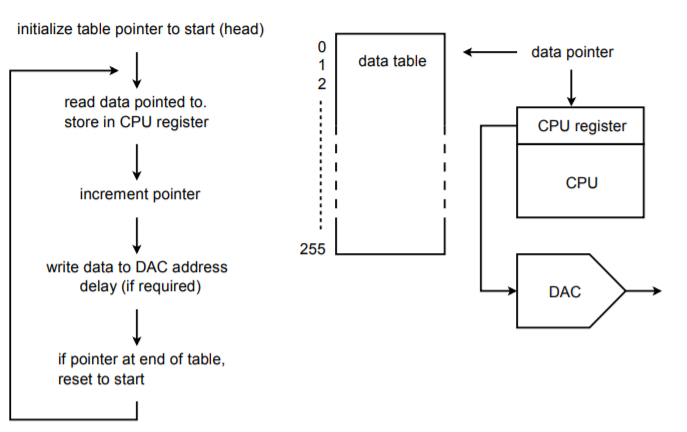
Abbildung \(\PageIndex{20}\): Arbiträrwellenform-Generator.
Bei der Initialisierung wird ein Adresszeiger auf die Startadresse der Datentabelle gesetzt. Über den Zeiger liest die CPU die Daten aus der Tabelle. Der Zeiger wird inkrementiert, so dass er nun auf das nächste Element in der Tabelle zeigt. (Einige CPUs bieten einen Post-Inkrement-Adressierungsmodus, so dass beide Schritte in einer einzigen Anweisung ausgeführt werden können.) Als nächstes schreibt die CPU die Daten an die spezielle DAC-Adresse. An diesem Punkt wird eine Art Software-/Hardware-Verzögerung ausgelöst, die die Ausgangsdatenrate festlegt. Nach der Verzögerung liest die CPU das nächste Datenelement über den Zeiger und fährt wie im ersten Durchlauf fort. Sobald das 256. Element ausgegeben wurde, wird der Zeiger auf den Anfang der Tabelle zurückgesetzt und der Vorgang wird fortgesetzt. Auf diese Weise kann man sich die Tabelle als zirkulär, also als unendlich, vorstellen. Wenn die Systemsoftware in einer höheren Programmiersprache geschrieben ist, kann die Zeiger-/Datentabelle als einfaches Array implementiert werden, bei dem der Array-Index durch einen Zähler gesetzt wird. Dies ist jedoch nicht so effizient wie ein direkter Ansatz auf Assembler-Ebene.
Das wirklich Schöne an diesem System ist, dass die Datentabelle praktisch jede beliebige Folge von Daten enthalten kann. Die Daten könnten einen Sinus, einen Impuls, ein Dreieck oder eine andere Standardfunktion darstellen. Noch wichtiger ist, dass die Daten eine Sinuswelle mit einem eingebetteten Rauschsignal oder ein Signal mit einer Brummkomponente darstellen können. Diese Daten können aus drei grundlegenden Quellen stammen. Erstens kann die Datentabelle durch direkte Berechnung gefüllt werden, wenn die Zeitbereichsgleichung der gewünschten Funktion bekannt ist. Zweitens könnten die Daten vom Benutzer durch irgendeine Form der Interaktion mit einem Computer hergestellt werden, vielleicht mit einer Maus oder einem Zeichenblock. Schließlich können die Daten auch aus einem realen Signal abgeleitet werden. Das heißt, ein Analog-Digital-Wandler kann verwendet werden, um das Signal in digitaler Form aufzuzeichnen. Die Daten können dann in die Tabelle geladen und wiederholt abgespielt werden. Der Arbiträrwellenform-Generator ermöglicht es seinem Benutzer, Schaltungen und Systeme mit einer Reihe von Wellenformen zu testen, die auf andere Weise unmöglich oder unpraktisch zu erzeugen wären.
Beispiel \(\PageIndex{3}\)
Unter Computersteuerung können DA-Wandler als Teil eines automatisierten Testgerätesystems verwendet werden. Um ein elektronisches Produkt vollständig zu charakterisieren, muss eine Reihe von Einzeltests durchgeführt werden. Das Einrichten jedes einzelnen Tests kann etwas zeitaufwendig sein und unterliegt der Gefahr von Bedienerfehlern. Durch die Automatisierung dieses Vorgangs kann die Wiederholbarkeit verbessert und die Testzeit verkürzt werden. Es gibt viele Möglichkeiten, wie dieser Prozess automatisiert werden kann. Wir sehen uns einen Ansatz an.
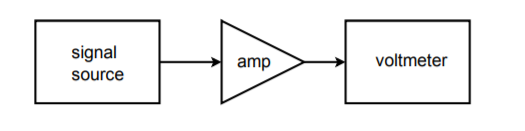
Abbildung (\PageIndex{21}\): Einfacher Testaufbau.
Angenommen, wir möchten Frequenzgangmessungen für einen Verstärker bei 20 verschiedenen Frequenzen durchführen. Ein für diese Aufgabe geeigneter Schaltungstestaufbau ist in Abbildung \(\PageIndex{21}\) dargestellt. Um diesen Test manuell durchzuführen, sind 20 verschiedene Einstellungen des Quellsignals und 20 entsprechende Ausgangsmesswerte erforderlich. Dies kann sich als recht mühsam erweisen, wenn viele Geräte getestet werden sollen. Es wäre sehr praktisch, wenn es eine Möglichkeit gäbe, die Quellfrequenz automatisch auf voreingestellte Werte zu ändern. Dies ist nicht besonders schwierig. Die meisten modernen Quellen haben Steuerspannungseingänge, die zur Einstellung der Frequenz verwendet werden können. Die erforderliche Steuerspannung kann mit Hilfe eines Computers und eines DA-Wandlers erzeugt und genau eingestellt werden. Der Computer kann so programmiert werden, dass er bestimmte digitale Wörter an den DAC sendet, der wiederum den Steuereingang der Signalquelle speist. Mit anderen Worten, das Datenwort stellt direkt die Frequenz der Signalquelle ein. Der Computer kann so programmiert werden, dass er praktisch jede beliebige Sequenz von Datenwörtern mit fast jeder Rate sendet, und das alles ohne Eingreifen des Bedieners. Der Bediener muss lediglich den Prozess starten. Die Wiederholbarkeit der Prüfung ist mit einem solchen System sehr hoch. Ein Blockdiagramm dieses Systems ist in Abbildung \(\PageIndex{22}\) dargestellt.
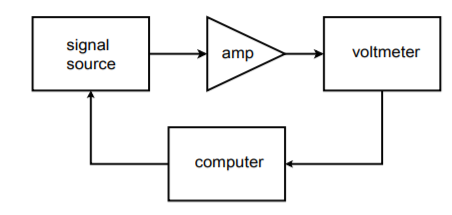
Abbildung \(\PageIndex{22}\): Automatisierter Testaufbau.
Um die Daten aufzuzeichnen, kann das Voltmeter an einen Streifenschreiber oder besser noch an den Computer angeschlossen werden. Die Daten können in digitaler Form an den Computer gesendet werden, wenn das Voltmeter eine fortschrittliche Konstruktion hat, oder, mit einem Analog-Digital-Wandler, kann das Ausgangssignal direkt abgetastet und vom Computer manipuliert werden. In beiden Fällen können Datendateien für jede geprüfte Einheit erstellt und für die spätere Verwendung gespeichert werden. Außerdem kann am Ende einer Testreihe schnell eine praktische statistische Analyse durchgeführt werden. Beachten Sie, dass, da der DA-Wandler nur ein Steuersignal erzeugt, normalerweise keine sehr hohe Auflösung und geringe Verzerrung erforderlich ist. Wenn ein hochauflösender Wandler verwendet wird, ist es möglich, die Testsignale im Computer zu erzeugen (wie beim Arbitrary-Funktionsgenerator) und auf die Signalquelle zu verzichten.
Das automatisierte Testsystem ist nur eine mögliche Anwendung der Gerätesteuerung. Ein weiteres interessantes Beispiel liegt in der Erzeugung von Laser-„Lichtspielen“. Ein Blockdiagramm eines vereinfachten Systems ist in Abbildung \(\PageIndex{23}\) dargestellt. Um die komplexen Muster zu erzeugen, die das Publikum sieht, wird ein Laserstrahl von winzigen beweglichen Spiegeln reflektiert. Die Spiegel können an einem einfachen Galvanometer angebracht sein. Das Galvanometer wird von einem DAC gespeist. Das Muster, das der Laserstrahl erzeugt, hängt davon ab, wie das Galvanometer den Spiegel bewegt, was wiederum von den Datenworten gesteuert wird, die dem DAC zugeführt werden. In der Praxis können mehrere Spiegel verwendet werden, um den Strahl entlang dreier Achsen abzulenken.
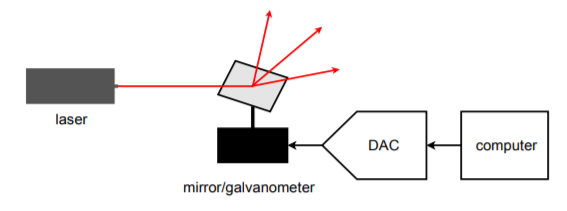
Abbildung (\PageIndex{23}\): Computergesteuerte Beleuchtung.
DA-Wandler können zur Einstellung jedes Geräts mit einem Eingang vom Typ Steuerspannung verwendet werden. Außerdem können sie zur Steuerung elektromechanischer Geräte verwendet werden, die auf eine angelegte Spannung reagieren. Ihr wirklicher Vorteil ist die Wiederholbarkeit und Flexibilität, die sie bieten.