Calcular el volumen
Esta página explica cómo calcular el volumen de los objetos sólidos, es decir, cuánto podría caber en un objeto si, por ejemplo, lo llenáramos con un líquido.
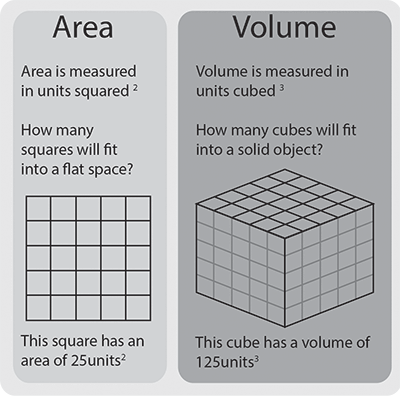
El área es la medida de cuánto espacio hay dentro de un objeto bidimensional (consulta nuestra página: Cálculo del área para saber más).
El volumen es la medida de cuánto espacio hay dentro de un objeto tridimensional. Nuestra página sobre formas tridimensionales explica los fundamentos de dichas formas.
En el mundo real, calcular el volumen probablemente no sea algo que utilices tan a menudo como calcular el área.
Sin embargo, puede seguir siendo importante. Ser capaz de calcular el volumen te permitirá, por ejemplo, calcular cuánto espacio de embalaje tienes cuando te mueves de casa, cuánto espacio de oficina necesitas o cuánta mermelada puedes meter en un tarro.
También puede ser útil para entender lo que los medios de comunicación quieren decir cuando hablan de la capacidad de una presa o del caudal de un río.
Atención a las unidades
El área se expresa en unidades cuadradas, porque son dos medidas multiplicadas.
El volumen se expresa en unidades cúbicas, porque es la suma de tres medidas (longitud, anchura y profundidad) multiplicadas. Las unidades cúbicas incluyen cm3, m3 y pies cúbicos.
¡AVISO!
El volumen también puede expresarse como capacidad de líquido.
Sistema métrico
En el sistema métrico la capacidad de líquido se mide en litros, lo que es directamente comparable con la medida cúbica, ya que 1ml = 1cm3. 1 litro = 1.000 ml = 1.000cm3.
Sistema imperial/inglés
En el sistema imperial/inglés las medidas equivalentes son onzas líquidas, pintas, cuartos de galón y galones, que no son fácilmente traducibles a pies cúbicos. Por lo tanto, es mejor ceñirse a las unidades de volumen de líquidos o de sólidos.
Para más información, consulte nuestra página sobre Sistemas de Medida
Fórmulas básicas para calcular el volumen
Volumen de sólidos de base rectangular

Mientras que la fórmula básica para el área de una forma rectangular es la longitud × la anchura, la fórmula básica para el volumen es la longitud × la anchura × la altura.
La forma de referirse a las diferentes dimensiones no cambia el cálculo: puedes, por ejemplo, utilizar «profundidad» en lugar de «altura». Lo importante es que las tres dimensiones se multiplican entre sí. Puedes multiplicar en el orden que quieras, ya que no cambiará la respuesta (consulta nuestra página sobre la multiplicación para saber más).
Una caja con las dimensiones de 15cm de ancho, 25cm de largo y 5cm de alto tiene un volumen de:
15 × 25 × 5 = 1875cm3
Volumen de Prismas y Cilindros
Esta fórmula básica se puede extender para cubrir el volumen de cilindros y prismas también. En lugar de un extremo rectangular, simplemente se tiene otra forma: un círculo para los cilindros, un triángulo, un hexágono o, de hecho, cualquier otro polígono para un prisma.
En efecto, para los cilindros y prismas, el volumen es el área de un lado multiplicada por la profundidad o la altura de la forma.
La fórmula básica para el volumen de prismas y cilindros es, por tanto:
Área de la forma del extremo × la altura/profundidad del prisma/cilindro.
Volumen de conos y pirámides
El mismo principio que el anterior (anchura × longitud × altura) es válido para calcular el volumen de un cono o una pirámide, excepto que, como llegan a un punto, el volumen es sólo una proporción del total que sería si continuaran con la misma forma hasta el final.
El volumen de un cono o una pirámide es exactamente un tercio del que tendría una caja o un cilindro con la misma base.
La fórmula es, por tanto:
Área de la base o forma final × la altura del cono/pirámide × 1/3
Vuelve a consultar nuestra página Calcular el área si no recuerdas cómo calcular el área de un círculo o un triángulo.
Por ejemplo, para calcular el volumen de un cono con un radio de 5cm y una altura de 10cm:
El área dentro de un círculo = πr2 (donde π (pi) es aproximadamente 3,14 y r es el radio del círculo).
En este ejemplo, área de la base (círculo) = πr2 = 3,14 × 5 × 5 = 78,5cm2.
78,5 × 10 = 785
785 × 1/3 = 261,6667cm3

Volumen de una esfera
Al igual que con un círculo, necesitas π (pi) para calcular el volumen de una esfera.
La fórmula es 4/3 × π × radio3.
Tal vez te preguntes cómo podrías calcular el radio de una esfera. A falta de clavarle una aguja de tejer (¡eficaz, pero terminal para la bola!), hay una forma más sencilla.
Puedes medir la distancia alrededor del punto más ancho de la esfera directamente, por ejemplo, con una cinta métrica. Este círculo es la circunferencia y tiene el mismo radio que la propia esfera.
La circunferencia de un círculo se calcula como 2 x π x radio.
Para calcular el radio a partir de la circunferencia se:
Divide la circunferencia por (2 x π).
Ejemplos trabajados: Cálculo del volumen
Ejemplo 1

Calcula el volumen de un cilindro con una longitud de 20cm, y cuyo extremo circular tiene un radio de 2,5cm.
En primer lugar, calcula el área de uno de los extremos circulares del cilindro.
El área de un círculo es πr2 (π × radio × radio). π (pi) es aproximadamente 3,14.
El área de un extremo es, por tanto:
3,14 x 2,5 x 2,5 = 19,63cm2
El volumen es el área de un extremo multiplicada por la longitud, y es por tanto:
19.63cm2 x 20cm = 392,70cm3

Ejemplo 2
¿Qué es más grande en volumen, una esfera de radio 2cm o una pirámide con base cuadrada de 2,5cm y altura de 10cm?
Primero, calcula el volumen de la esfera.
El volumen de una esfera es 4/3 × π × radio3.
El volumen de la esfera es, por tanto:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51cm3
A continuación, calcula el volumen de la pirámide.
El volumen de una pirámide es 1/3 × área de la base × altura.
Área de la base = longitud × anchura = 2,5cm × 2,5cm = 6,25cm2
El volumen es, por tanto, 1/3 x 6,25 × 10 = 20,83cm3
La esfera es, por tanto, mayor en volumen que la pirámide.
Calcular el volumen de los sólidos irregulares
Así como puedes calcular el área de las formas bidimensionales irregulares dividiéndolas en regulares, puedes hacer lo mismo para calcular el volumen de los sólidos irregulares. Sólo tienes que dividir el sólido en partes más pequeñas hasta que llegues sólo a sólidos con los que puedas trabajar fácilmente.
Ejemplo trabajado
Calcular el volumen de un cilindro de agua con altura total de 1m, diámetro de 40cm, y cuya sección superior es semiesférica.

Primero se divide la forma en dos secciones, un cilindro y una semiesfera (media esfera).
El volumen de una esfera es 4/3 × π × radio3. En este ejemplo el radio es de 20 cm (la mitad del diámetro). Como la parte superior es semiesférica, su volumen será la mitad del de una esfera completa. El volumen de esta sección de la forma, por tanto:
0,5 × 4/3 × π × 203 = 16.755,16cm3
El volumen de un cilindro es área de la base × altura. Aquí, la altura del cilindro es la altura total menos el radio de la esfera, que es 1m – 20cm = 80cm. El área de la base es πr2.
El volumen de la sección cilíndrica de esta forma es, por tanto:
80 × π × 20 × 20 = 100.530,96cm3
El volumen total de este recipiente de agua es, por tanto:
100.530,96 + 16.755,16 = 117.286,12cm3.
Este es un número bastante grande, por lo que puedes preferir convertirlo en 117,19 litros dividiéndolo por 1.000 (ya que hay 1000cm3 en un litro). Sin embargo, es bastante correcto expresarlo como cm3 ya que el problema no pide que la respuesta se exprese de ninguna forma en particular.
En conclusión…
Usando estos principios, si es necesario, ahora deberías ser capaz de calcular el volumen de casi cualquier cosa en tu vida, ya sea una caja de embalaje, una habitación o una bombona de agua.