Departamento de Ciencia y Tecnología de la Computación
¿Qué es una máquina de Turing?
Una máquina de Turing es una máquina hipotética pensada por el matemático Alan Turing en 1936. A pesar de su simplicidad, la máquina puede simular CUALQUIER algoritmo informático, por complicado que sea.

Arriba hay una representación muy simple de una máquina de Turing. Consiste en una cinta de longitud infinita que actúa como la memoria de un ordenador típico, o cualquier otra forma de almacenamiento de datos. Las casillas de la cinta suelen estar en blanco al principio y pueden escribirse con símbolos. En este caso, la máquina sólo puede procesar los símbolos 0 y 1 y » » (en blanco), por lo que se dice que es una máquina de Turing de 3 símbolos.
En todo momento, la máquina tiene un cabezal que se sitúa sobre uno de los cuadrados de la cinta. Con este cabezal, la máquina puede realizar tres operaciones muy básicas:
- Leer el símbolo del cuadrado que está bajo el cabezal.
- Editar el símbolo escribiendo un nuevo símbolo o borrándolo.
- Desplazar la cinta a la izquierda o a la derecha una casilla para que la máquina pueda leer y editar el símbolo de una casilla vecina.
Una demostración sencilla
Como ejemplo trivial para demostrar estas operaciones, vamos a intentar imprimir los símbolos «1 1 0» en una cinta inicialmente en blanco:

Primero, escribimos un 1 en la casilla que está debajo de la cabeza:

A continuación, movemos la cinta una casilla hacia la izquierda:

Ahora, escribe un 1 en el nuevo cuadrado bajo la cabeza:

A continuación, volvemos a mover la cinta hacia la izquierda una casilla:

Por último, escribe un 0 y ¡ya está!

Un programa sencillo
Con los símbolos «1 1 0» impresos en la cinta, vamos a intentar convertir los 1s en 0s y viceversa. Esto se llama inversión de bits, ya que los 1s y los 0s son bits en binario. Esto se puede hacer pasando las siguientes instrucciones a la máquina de Turing, utilizando la capacidad de lectura de la máquina para decidir sus operaciones posteriores por sí misma. Estas instrucciones conforman un programa sencillo.
| Símbolo leído | Instrucción de escritura | Instrucción de movimiento |
|---|---|---|
| En blanco | Nada | Nada |
| 0 | Escribir 1 | Mover la cinta a la derecha | 1 | Escribir 0 | Mover la cinta a la derecha |
La máquina leerá primero el símbolo que hay debajo del cabezal, escribirá un nuevo símbolo en consecuencia, luego moverá la cinta a la izquierda o a la derecha según las instrucciones, antes de repetir la secuencia de lectura-escritura-movimiento de nuevo.
Veamos lo que este programa hace a nuestra cinta desde el punto final anterior de las instrucciones:

El símbolo actual bajo el cabezal es 0, por lo que escribimos un 1 y movemos la cinta a la derecha una casilla.
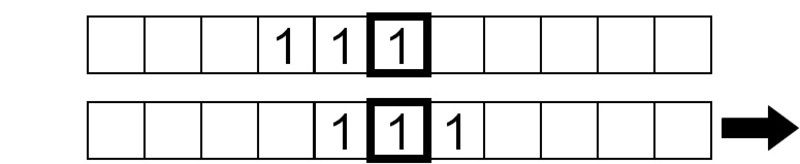
El símbolo que se está leyendo ahora es un 1, así que escribimos un 0 y movemos la cinta hacia la derecha una casilla:
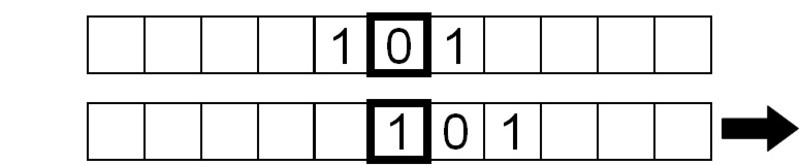
De forma similar, el símbolo leído es un 1, así que repetimos las mismas instrucciones.
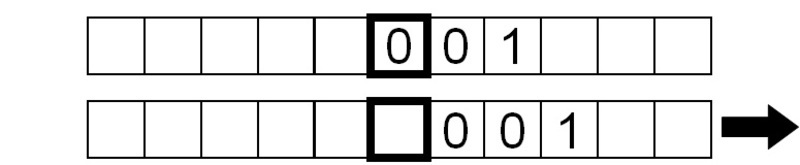
Por último, se lee un símbolo ‘en blanco’, por lo que la máquina no hace nada aparte de leer el símbolo en blanco continuamente ya que le hemos ordenado que repita la secuencia de lectura-escritura-movimiento sin parar.
De hecho, el programa está incompleto. Cómo hace la máquina para repetir la secuencia sin parar, y cómo hace la máquina para dejar de ejecutar el programa? El programa se lo indica con el concepto de estado de la máquina.
El estado de la máquina
Para completar el programa, hay que considerar los cambios de estado durante la ejecución del programa en la máquina. Los siguientes cambios, marcados en cursiva, deben añadirse a nuestra tabla que ahora puede llamarse tabla de estados:
| Estado | Símbolo leído | Instrucción de escritura | Instrucción de movimiento | Siguiente estado |
|---|---|---|---|---|
| Estado 0 | En blanco | Nada | Estado de parada | 0 | Escribir 1 | Mover la cinta hacia la derecha | Estado 0 |
| 1 | Escribir 0 | Mover la cinta hacia la derecha | Estado 0 |
Asignamos el conjunto anterior de instrucciones a un estado de la máquina, para que la máquina realice esas instrucciones cuando esté en el estado especificado.
Después de cada instrucción, también especificamos un estado para que la máquina haga la transición. En el ejemplo, la máquina es redirigida a su estado original, el estado 0, para repetir la secuencia de lectura-escritura-novela, a menos que se lea un símbolo en blanco. Cuando la máquina lee un símbolo en blanco, la máquina es dirigida a un estado de parada y el programa termina.
Máquinas de estados finitos
Aunque parezca una tontería hacerlo, vamos a añadir ahora un estado adicional a nuestro programa que revierta los bits «1 1 0» ya invertidos de nuevo de «0 0 1» a «1 1 0». A continuación se muestra la tabla actualizada, con los cambios listados en cursiva. La máquina de Turing se comporta ahora como una máquina de estados finitos con dos estados -se denominan máquinas de Turing de tres símbolos y dos estados-.
| Estado | Símbolo leído | Escritura instrucción | Instrucción de movimiento | Siguiente estado |
|---|---|---|---|---|
| Estado 0 | En blanco | Escribir en blanco | Mueve la cinta hacia la izquierda | Estado 1 |
| 0 | Escribe 1 | Mover la cinta hacia la derecha | Estado 1 | |
| 1 | Escribir 0 | Mover la cinta hacia la derecha | Estado 0 | |
| Estado 1 | En blanco | Escribir en blanco | Mover la cinta a la derecha | Estado de parada |
| 0 | Escribir 1 | Mover la cinta hacia la izquierda | Estado 1 | |
| 1 | Escribir 0 | Mover la cinta hacia la izquierda | Estado 1 |
Para la instrucción de escritura, «None» se ha cambiado por «Write blank» por uniformidad (para que sólo se haga referencia a los símbolos de la máquina), y hay que tener en cuenta que son equivalentes.
En lugar de una tabla de estados, el programa también se puede representar con un diagrama de estados:
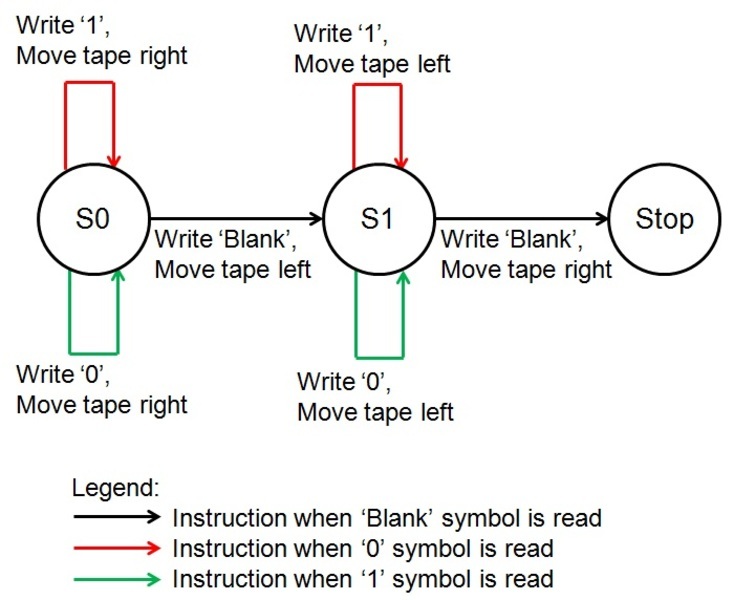
Desde donde estaba el programa anteriormente, en lugar de no hacer nada y detenerse después de que la máquina encuentre un símbolo en blanco, le indicamos que mueva la cinta hacia la izquierda antes de hacer la transición al estado 1, donde invierte el proceso de inversión de bits.
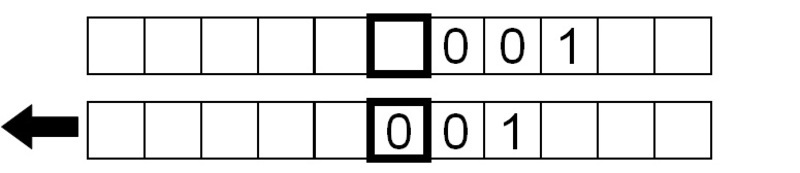
A continuación, invertimos los bits de nuevo, esta vez moviendo la cinta a la izquierda en lugar de a la derecha.
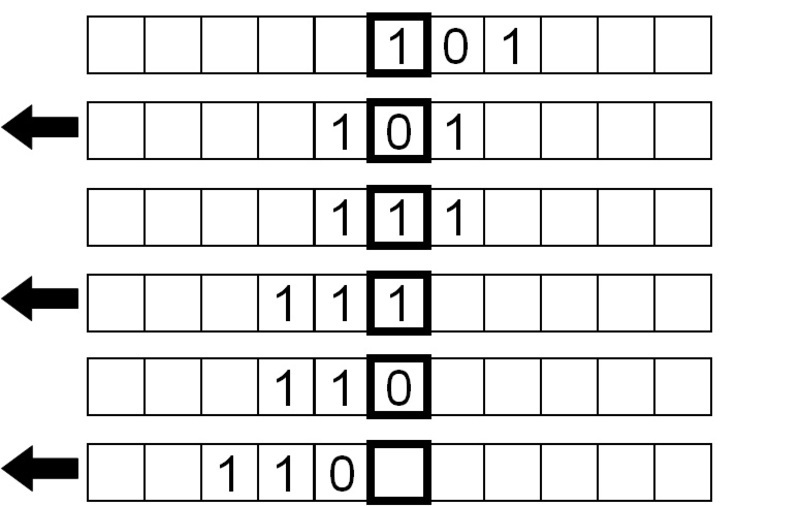
Finalmente, se lee un símbolo en blanco, así que movemos la cinta hacia la derecha para volver al punto de partida, y detenemos el programa.¡

Con la introducción de más estados en nuestro programa, podemos instruir a la máquina de Turing para que realice funciones más complejas y, por lo tanto, ejecute cualquier algoritmo que pueda realizar un ordenador de hoy en día.
En la sección dos, vamos a aprender sobre LEDs, pines GPIO, resistencias y python, antes de embarcarnos en la construcción de nuestra máquina de Turing!