Guías y consejos online de preparación para el SAT / ACT
Si estás estudiando trigonometría o cálculo -o te estás preparando para ello- tendrás que familiarizarte con el círculo unitario. El círculo unitario es una herramienta esencial utilizada para resolver el seno, el coseno y la tangente de un ángulo. Pero, ¿cómo funciona? Y ¿qué información necesitas saber para utilizarlo?
En este artículo, te explicamos qué es el círculo unitario y por qué deberías conocerlo. También te damos tres consejos para que recuerdes cómo utilizar el círculo unitario.
Imagen de portada: Gustavb/Wikimedia
El círculo unitario: Una introducción básica
El círculo unitario es un círculo con un radio de 1. Esto significa que para cualquier línea recta trazada desde el punto central del círculo a cualquier punto a lo largo del borde del círculo, la longitud de esa línea siempre será igual a 1. (Esto también significa que el diámetro del círculo será igual a 2, ya que el diámetro es igual al doble de la longitud del radio.)
Típicamente, el punto central del círculo unitario es donde se cruzan el eje x y el eje y, o en las coordenadas (0, 0):
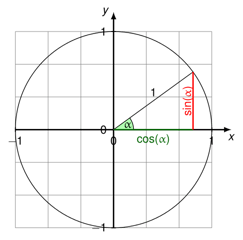
El círculo unitario, o círculo trigonométrico como también se le conoce, es útil de conocer porque nos permite calcular fácilmente el coseno, el seno y la tangente de cualquier ángulo entre 0° y 360° (o 0 y 2π radianes).
Como puedes ver en el diagrama anterior, al dibujar un radio en cualquier ángulo (marcado con ∝ en la imagen), estarás creando un triángulo rectángulo. En este triángulo, el coseno es la línea horizontal, y el seno es la línea vertical. En otras palabras, coseno = coordenada x, y seno = coordenada y. (La línea más larga del triángulo, o hipotenusa, es el radio y por tanto es igual a 1.)
¿Por qué es importante todo esto? Recuerda que puedes resolver las longitudes de los lados de un triángulo utilizando el teorema de Pitágoras, o $a^2+b^2=c^2$ (en el que a y b son las longitudes de los lados del triángulo, y c es la longitud de la hipotenusa).
Sabemos que el coseno de un ángulo es igual a la longitud de la recta horizontal, el seno es igual a la longitud de la recta vertical, y la hipotenusa es igual a 1. Por tanto, podemos decir que la fórmula de cualquier triángulo rectángulo en la circunferencia unitaria es la siguiente:
$cos^2θ+\sin^2θ=1^2$
Dado que $1^2=1$, podemos simplificar esta ecuación así:
$cos^2θ+\sin^2θ=1$
Ten en cuenta que estos valores pueden ser negativos dependiendo del ángulo formado y de en qué cuadrante se encuentren las coordenadas x e y (más adelante lo explicaré con más detalle).
Aquí tienes un resumen de todos los ángulos principales en grados y radianes del círculo unitario:
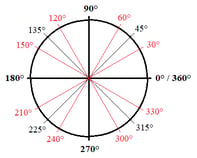
Círculo unitario – Grados
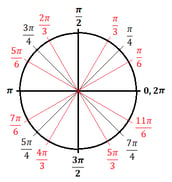
Círculo unitario – Radianes
¿Pero qué pasa si no hay ningún triángulo formado? Veamos qué ocurre cuando el ángulo es de 0º, creando una recta horizontal a lo largo del eje x:
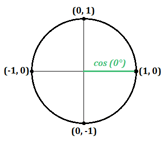
En esta recta, la coordenada x es igual a 1 y la coordenada y es igual a 0. Sabemos que el coseno es igual a la coordenada x, y el seno es igual a la coordenada y, por lo que podemos escribir esto:
- $\cos0°=1$
- $\sin0°=0$
- $\cos90°=0$
- $\sin90°=1$
- $1/2$
- ${√2}/2$
- ${√3}/2$
- Línea horizontal o vertical corta = $1/2$
- Línea horizontal o vertical media = ${√2}/2$
- Línea horizontal o vertical larga = ${√3}/2$
- 30° / $π/6$
- 45° / $π/4$
- 60° / $π/3$
¿Y si el ángulo es de 90° y hace una línea perfectamente vertical a lo largo del eje y?
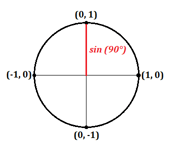
Aquí podemos ver que la coordenada x es igual a 0 y la coordenada y es igual a 1. Esto nos da los siguientes valores para el seno y el coseno:
Este eslogan se aplica definitivamente si no eres un amante de las matemáticas.
Por qué deberías conocer el círculo unitario
Como se ha dicho, el círculo unitario es útil porque nos permite resolver fácilmente el seno, coseno o tangente de cualquier grado o radián. Es especialmente útil conocer la gráfica del círculo unitario si necesitas resolver ciertos valores trigonométricos para los deberes de matemáticas o si te estás preparando para estudiar cálculo.
Pero, ¿cómo puede ayudarte exactamente conocer el círculo unitario? Supongamos que te dan el siguiente problema en un examen de matemáticas -y que no te permiten usar una calculadora para resolverlo:
$\sin30°$
¿Por dónde empiezas? Volvamos a ver el gráfico del círculo unitario, esta vez con todos los ángulos mayores (tanto en grados como en radianes) y sus coordenadas correspondientes:
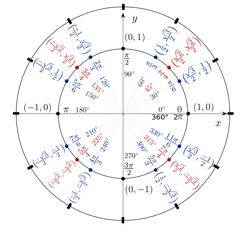Jim.belk/Wikimedia
¡No te agobies! Recuerda que todo lo que estás resolviendo es $\sin30°$. Mirando esta gráfica, podemos ver que la coordenada y es igual a $1/2$ a 30°. Y como la coordenada y es igual al seno, nuestra respuesta es la siguiente:
$\sin30°=1/2$
¿Pero qué pasa si tienes un problema que utiliza radianes en lugar de grados? El proceso para resolverlo sigue siendo el mismo. Digamos, por ejemplo, que tienes un problema parecido a este:
$\cos{{3π}/4}$
De nuevo, usando la tabla anterior, podemos ver que la coordenada x (o coseno) para ${3π}/4$ (que es igual a 135°) es $-{√2}/2$. Así es como quedaría nuestra respuesta a este problema entonces:
$\cos({3π}/4)=-{√2}/2$
Todo esto es bastante fácil si tienes la carta del círculo unitario de arriba para usarla como referencia. Pero la mayoría de las veces (por no decir todas) no será así, y se espera que respondas a este tipo de preguntas matemáticas utilizando únicamente tu cerebro.
¿Así que cómo puedes recordar el círculo unitario? Sigue leyendo para conocer nuestros mejores consejos!
Cómo recordar el círculo unitario: 3 consejos esenciales
En esta sección, te damos nuestros mejores consejos para recordar el círculo trigonométrico para que puedas utilizarlo con facilidad en cualquier problema de matemáticas que lo requiera.
No recomendaría practicar el círculo unitario con post-its, pero, oye, es un comienzo.
#1: Memoriza los ángulos y coordenadas comunes
Para poder utilizar el círculo unitario de forma efectiva, necesitarás memorizar los ángulos más comunes (tanto en grados como en radianes), así como sus correspondientes coordenadas x e y.
El diagrama de arriba es una tabla de círculos unitarios útil para mirar, ya que incluye todos los ángulos principales tanto en grados como en radianes, además de sus correspondientes puntos de coordenadas a lo largo de los ejes x e y.
Aquí hay un gráfico que recoge esta misma información en forma de tabla:
|
Ángulo (Grados)
|
Ángulo (Radianes)
|
Coordenadas del punto en el círculo
|
|
0° / 360°
|
0 / 2π
|
(1, 0)
|
|
30°
|
$π/6$
|
$({√3}/2, 1/2)$
|
|
45°
|
$π/4$
|
$({√2}/2, {√2}/2)$
|
|
60°
|
π/3$
|
$(1/2,{√3}/2)$
|
|
90°
|
d/2$ |
(0, 1)
|
|
120°
|
${2π}/3$
|
$(-1/2, {√3}/2)$
|
|
135°
|
${3π}/4$
|
$(-{√2}/2, {√2}/2)$
|
|
150°
|
${5π}/6$
|
$(-{√3}/2, 1/2)$
|
180°
|
π
|
(-1, 0)
|
210°
|
${7}/6$
|
$(-{√3}/2, -1/2)$
|
225°
|
${5π}/4$
|
$(-{√2}/2, -{√2}/2)$
|
240°
|
${4π}/3$
|
$(-1/2, -{√3}/2)$
|
270°
|
${3π}/2$
|
(0, -1)
|
300°
|
${5π}/3$
|
$(1/2, -{√3}/2)$
|
315°
|
${7π}/4$
|
$({√2}/2, -{√2}/2)$
|
330°
|
{11π}/6$
|
$({√3}/2, -1/2)$
|
Ahora, aunque eres más que bienvenido a tratar de memorizar todas estas coordenadas y ángulos, esto es un montón de cosas para recordar.
Afortunadamente, hay un truco que puedes utilizar para ayudarte a recordar las partes más importantes del círculo unitario.
Mira las coordenadas de arriba y notarás un patrón claro: todos los puntos (excluyendo los de 0°, 90°, 270° y 360°) alternan entre sólo tres valores (ya sean positivos o negativos):
Cada valor corresponde a una línea corta, media o larga tanto para el coseno como para el seno:
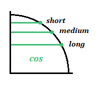
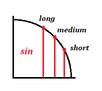
Aquí tienes el significado de estas longitudes:
Por ejemplo, si estás intentando resolver $\cos{π/3}$, debes saber enseguida que este ángulo (que es igual a 60°) indica una línea horizontal corta en el círculo unitario. Por tanto, su correspondiente coordenada x debe ser igual a $1/2$ (un valor positivo, ya que $π/3$ crea un punto en el primer cuadrante del sistema de coordenadas).
Por último, aunque es útil memorizar todos los ángulos de la tabla anterior, ten en cuenta que, con diferencia, los ángulos más importantes que hay que recordar son los siguientes:
Trata tus negativos y positivos como si fueran cables que pueden potencialmente matarte si están mal conectados.
#2: Aprende lo que es negativo y lo que es positivo
Es fundamental poder distinguir las coordenadas x e y positivas y negativas para encontrar el valor correcto en un problema de trigonometría. Como recordatorio, el hecho de que una coordenada en el círculo unitario sea positiva o negativa depende del cuadrante (I, II, III o IV) en el que se encuentre el punto:
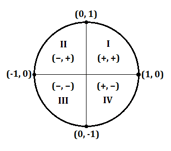
Aquí tienes una tabla que muestra si una coordenada será positiva o negativa en función del cuadrante en el que se encuentre un determinado ángulo (en grados o radianes):
|
Cuadrante
|
Coordenada X (Coseno)
|
Y-.Coordenada (Seno)
|
I
|
+
|
+
|
|
II
|
–
|
+
|
III
|
–
|
–
|
|
IV
|
+
|
Por ejemplo, digamos que te dan el siguiente problema en un examen de matemáticas:
$cos210°$
Antes de intentar resolverlo, deberías ser capaz de reconocer que la respuesta será un número negativo ya que el ángulo 210° cae en el cuadrante III (donde las coordenadas x son siempre negativas).
Ahora, usando el truco que aprendimos en el consejo 1, puedes averiguar que un ángulo de 210° crea una línea horizontal larga. Por tanto, nuestra respuesta es la siguiente:
$\cos210°=-{√3}/2$
#3: Saber resolver la tangente
Por último, es fundamental saber utilizar toda esta información sobre el círculo trigonométrico y el seno y coseno para poder resolver la tangente de un ángulo.
En trigonometría, para hallar la tangente de un ángulo θ (ya sea en grados o en radianes), basta con dividir el seno entre el coseno:
$tanθ={\sinθ}/{\cosθ}$
Por ejemplo, digamos que intentas responder a este problema:
$\tan300°$
El primer paso es plantear una ecuación en términos de seno y coseno:
$\tan300°={\sin300°}/{cos300°}$
Ahora, para resolver la tangente, necesitamos encontrar el seno y el coseno de 300°. Deberías ser capaz de reconocer rápidamente que el ángulo 300° cae en el cuarto cuadrante, lo que significa que el coseno, o coordenada x, será positivo, y el seno, o coordenada y, será negativo.
También debes saber de inmediato que el ángulo 300° crea una línea horizontal corta y una línea vertical larga. Por tanto, el coseno (la recta horizontal) será igual a $1/2$, y el seno (la recta vertical) será igual a $-{√3}/2$ (un valor y negativo, ya que este punto está en el cuadrante IV).
Ahora, para encontrar la tangente, sólo hay que enchufar y resolver:
$\tan300°={-{√3}/2}/{1/2}$
$\tan300°=-√3$
¡Es hora de poner en práctica tus habilidades matemáticas!
Conjunto de preguntas de práctica del círculo unitario
Ahora que sabes cómo es el círculo unitario y cómo utilizarlo, vamos a poner a prueba lo que has aprendido con unos cuantos problemas de práctica.
Preguntas
- $sin45°$
- $cos240°$
- $cos{5π}/3$
- $tan{2π}/3$
Respuestas
- ${√2}/2$
- $-1/2$
- $1/2$
- $-√3$
Explicaciones de las respuestas
#1: $\sin45°$
Con este problema, hay dos datos que deberías poder identificar enseguida:
- La respuesta será positiva, ya que el ángulo 45° está en el cuadrante I, y el seno de un ángulo es igual a la coordenada y
- El ángulo 45° crea una recta vertical de longitud media (para el seno)
Dado que 45° indica una recta positiva y de longitud media, la respuesta correcta es ${√2}/2$.
Si no estás seguro de cómo resolverlo, dibuja un diagrama que te ayude a determinar si la longitud de la recta será corta, media o larga.
#2: $\cos240°$
Al igual que el problema #1 anterior, hay dos datos que deberías poder captar rápidamente con este problema:
- La respuesta será negativa, ya que el ángulo 240° está en el cuadrante III, y el coseno de un ángulo es igual a la coordenada x
- El ángulo 240° crea una línea horizontal corta (para el coseno)
Dado que 240° indica una línea negativa y corta, la respuesta correcta es $-1/2$.
#3: $\cos{5π}/3$
A diferencia de los problemas anteriores, este problema utiliza radianes en lugar de grados. Aunque esto puede hacer que el problema parezca más complicado de resolver, en realidad utiliza los mismos pasos básicos que los otros dos problemas.
En primer lugar, debes reconocer que el ángulo ${5π}/3$ está en el cuadrante IV, por lo que la coordenada x, o coseno, será un número positivo. También deberías ser capaz de decir que ${5π}/3$ crea una línea horizontal corta.
Esto te da suficiente información para determinar que la respuesta es $1/2$.
#4: $\tan{2π}/3$
Este problema trata de la tangente en lugar del seno o coseno, lo que significa que requerirá un poco más de matemáticas por nuestra parte. En primer lugar, recordemos la fórmula básica para hallar la tangente:
$\tan θ={sin θ}/{cos θ}$
Ahora, tomemos el grado que nos han dado-{2π}/3$-y pongámoslo en esta ecuación:
$tan {2π}/3={sin {2π}/3}/{cos {2π}/3}$
Ahora deberías ser capaz de resolver el seno y el coseno por separado usando lo que has memorizado sobre el círculo unitario. Como el ángulo ${2π}/3$ está en el cuadrante II, la coordenada x (o coseno) será negativa, y la coordenada y (o seno) será positiva.
A continuación, deberías ser capaz de determinar basándote sólo en el ángulo que la línea horizontal es una línea corta, y la línea vertical es una línea larga. Esto significa que el coseno es igual a $-1/2$, y el seno es igual a ${√3}/2$.
Ahora que hemos averiguado estos valores, sólo tenemos que introducirlos en nuestra ecuación inicial y resolver la tangente:
$tan {2π}/3={√3}/2}/{-1/2}$
$tan {2π}/3=-√3$
¿Qué sigue?
Si vas a presentarte al SAT o al ACT próximamente, necesitarás saber algo de trigonometría para poder hacerlo bien en la sección de matemáticas. Echa un vistazo a nuestras guías de expertos sobre la trigonometría en el SAT y el ACT para que puedas aprender exactamente lo que necesitarás saber para el día del examen!
Además de memorizar el círculo de la unidad, es una buena idea aprender cómo enchufar números y cómo enchufar respuestas. Lee nuestras guías para aprender todo sobre estas dos útiles estrategias, que puedes usar en cualquier examen de matemáticas -¡incluyendo el SAT y el ACT!
¿Tienes amigos que también necesitan ayuda con la preparación del examen? ¡Comparte este artículo!
Hannah recibió su maestría en Estudios Japoneses de la Universidad de Michigan y tiene una licenciatura de la Universidad del Sur de California. De 2013 a 2015, enseñó inglés en Japón a través del programa JET. Es una apasionada de la educación, la escritura y los viajes.