Fachbereich Informatik und Technik
Was ist eine Turing-Maschine?
Eine Turing-Maschine ist eine hypothetische Maschine, die 1936 von dem Mathematiker Alan Turing erdacht wurde. Trotz ihrer Einfachheit kann die Maschine JEDEN Computeralgorithmus simulieren, egal wie kompliziert er ist!

Oben ist eine sehr einfache Darstellung einer Turing-Maschine. Sie besteht aus einem unendlich langen Band, das wie der Speicher in einem typischen Computer oder einer anderen Form der Datenspeicherung funktioniert. Die Quadrate auf dem Band sind normalerweise am Anfang leer und können mit Symbolen beschrieben werden. In diesem Fall kann die Maschine nur die Symbole 0 und 1 sowie “ “ (Leerzeichen) verarbeiten und wird daher als 3-Symbol-Turing-Maschine bezeichnet.
Zu jedem Zeitpunkt hat die Maschine einen Kopf, der über einem der Quadrate auf dem Band positioniert ist. Mit diesem Kopf kann die Maschine drei sehr grundlegende Operationen durchführen:
- Lesen Sie das Symbol auf dem Quadrat unter dem Kopf.
- Bearbeiten Sie das Symbol, indem Sie ein neues Symbol schreiben oder es löschen.
- Bewegen Sie das Band um ein Quadrat nach links oder rechts, so dass die Maschine das Symbol auf einem Nachbarfeld lesen und bearbeiten kann.
Eine einfache Demonstration
Als triviales Beispiel, um diese Operationen zu demonstrieren, wollen wir versuchen, die Symbole „1 1 0“ auf ein zunächst leeres Band zu drucken:

Zunächst schreiben wir eine 1 auf das Quadrat unter dem Kopf:

Nächstens bewegen wir das Band um ein Quadrat nach links:

Nun schreiben wir eine 1 auf das neue Quadrat unter dem Kopf:

Dann bewegen wir das Band wieder um ein Quadrat nach links:

Schließlich schreiben wir eine 0 und das war’s!

Ein einfaches Programm
Mit den auf dem Band aufgedruckten Symbolen „1 1 0“ wollen wir nun versuchen, die 1en in 0en umzuwandeln und umgekehrt. Das nennt man Bit-Invertierung, da 1en und 0en im Binärsystem Bits sind. Dies kann geschehen, indem man die folgenden Anweisungen an die Turing-Maschine übergibt und die Lesefähigkeiten der Maschine nutzt, um die nachfolgenden Operationen selbständig zu entscheiden. Diese Anweisungen bilden ein einfaches Programm.
| Symbol lesen | Anweisung schreiben | Befehl bewegen |
|---|---|---|
| Leerzeichen | Keine | Keine |
| 0 | Schreiben 1 | Band nach rechts verschieben |
| 1 | Schreiben 0 | Band nach rechts verschieben |
Das Gerät liest zuerst das Symbol unter dem Kopf, schreibt entsprechend ein neues Symbol, bewegt dann das Band nach links oder rechts, wie angewiesen, bevor sie die Lese-Schreib-Bewegung-Sequenz erneut wiederholt.
Lassen Sie uns sehen, was dieses Programm mit unserem Band ab dem vorherigen Endpunkt der Anweisungen macht:

Das aktuelle Symbol unter dem Kopf ist 0, also schreiben wir eine 1 und verschieben das Band um ein Feld nach rechts.
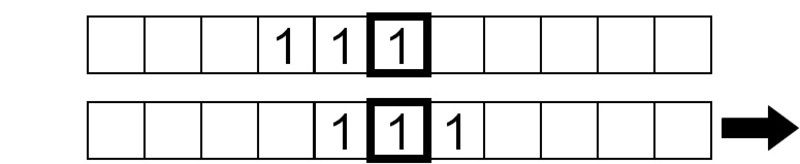
Das zu lesende Symbol ist jetzt 1, also schreiben wir eine 0 und verschieben das Band um ein Feld nach rechts:
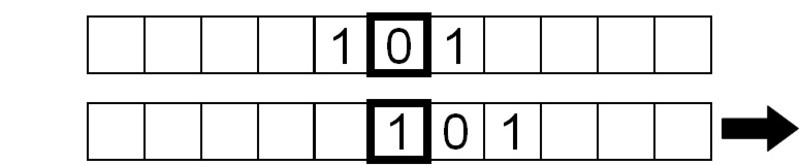
Auch das gelesene Symbol ist eine 1, also wiederholen wir die gleichen Anweisungen.
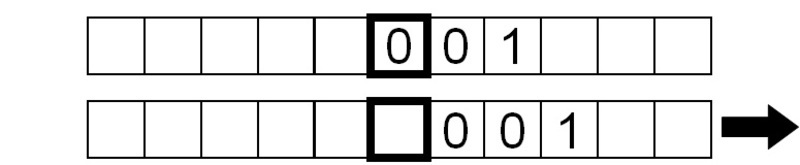
Schließlich wird ein ‚leeres‘ Symbol gelesen, also tut die Maschine nichts anderes, als das leere Symbol kontinuierlich zu lesen, da wir sie angewiesen haben, die Lese-Schreib-Bewegung-Sequenz ohne Unterbrechung zu wiederholen.
In der Tat ist das Programm unvollständig. Wie kann die Maschine die Sequenz endlos wiederholen, und wie kann die Maschine aufhören, das Programm auszuführen? Das Programm sagt es ihr mit dem Konzept des Maschinenzustands.
Der Maschinenzustand
Um das Programm zu vervollständigen, müssen die Zustandsänderungen während der Ausführung des Programms auf der Maschine berücksichtigt werden. Die folgenden, kursiv markierten Änderungen müssen in unsere Tabelle eingefügt werden, die nun als Zustandstabelle bezeichnet werden kann:
| Zustand | Symbol lesen | Schreibbefehl | Bewegebefehl | Nächster Zustand | |
|---|---|---|---|---|---|
| Zustand 0 | Leerzeichen | Keine | Keine | Stopzustand | |
| 0 | Schreiben 1 | Band nach rechts verschieben | Zustand 0 | 1 | Schreiben 0 | Band nach rechts verschieben | Zustand 0 |
Wir ordnen den vorherigen Satz von Anweisungen einem Maschinenzustand zu, so dass die Maschine diese Anweisungen ausführt, wenn sie sich in dem angegebenen Zustand befindet.
Nach jeder Anweisung geben wir auch einen Zustand an, in den die Maschine übergehen soll. Im Beispiel wird die Maschine in ihren ursprünglichen Zustand, Zustand 0, zurückgeführt, um die Lese-Schreib-Nut-Sequenz zu wiederholen, es sei denn, es wird ein leeres Symbol gelesen. Wenn die Maschine ein leeres Symbol liest, wird die Maschine in einen Stop-Zustand geleitet und das Programm wird beendet.
Finite state machines
Auch wenn es albern erscheint, fügen wir nun einen zusätzlichen Zustand zu unserem Programm hinzu, der die bereits invertierten Bits „1 1 0“ wieder von „0 0 1“ auf „1 1 0“ zurückführt. Unten sehen Sie die aktualisierte Tabelle, wobei die Änderungen kursiv dargestellt sind. Der Turing-Automat verhält sich nun wie ein endlicher Automat mit zwei Zuständen – man nennt ihn Drei-Symbol-Zwei-Zustands-Turing-Automat.
| Zustand | Symbol lesen | Schreiben Anweisung | Anweisung verschieben | Nächster Zustand |
|---|---|---|---|---|
| Zustand 0 | Leerzeichen | Schreiben Leerzeichen | Band nach links verschieben | Zustand 1 |
| 0 | Schreiben 1 | Band nach rechts verschieben | Status 1 | |
| 1 | Schreiben 0 | Band nach rechts verschieben Band nach rechts | Status 0 | |
| Status 1 | Leerzeichen | Leerzeichen schreiben | Band nach rechts bewegen | Zustand anhalten |
| 0 | Schreiben 1 | Band nach links bewegen | Zustand 1 | |
| 1 | Schreiben 0 | Band nach links bewegen | Zustand 1 |
Für den Schreibbefehl, „None“ wurde der Einheitlichkeit halber (damit nur auf die Symbole der Maschine Bezug genommen wird) in „Write blank“ geändert, wobei zu beachten ist, dass diese gleichwertig sind.
Anstatt einer Zustandstabelle kann das Programm auch mit einem Zustandsdiagramm dargestellt werden:
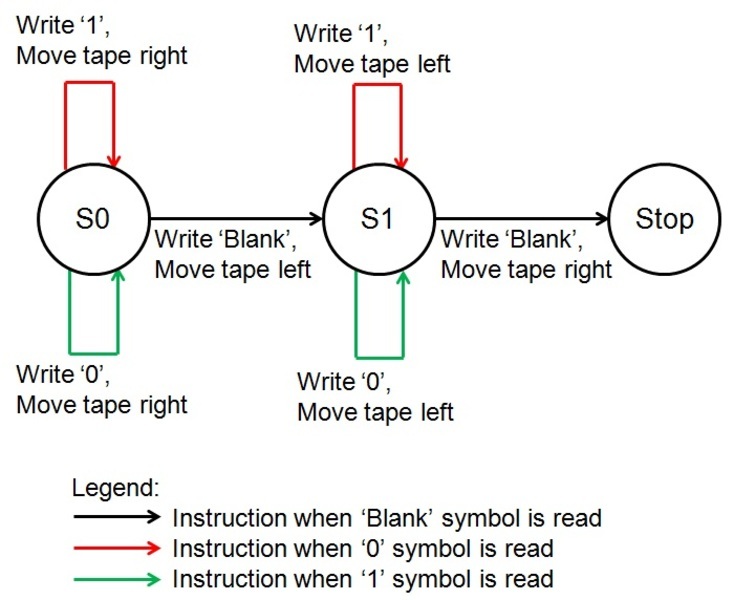
Anstatt an der Stelle, an der sich das Programm vorher befand, nichts zu tun und anzuhalten, nachdem der Automat auf ein leeres Symbol gestoßen ist, weisen wir ihn an, das Band nach links zu bewegen, bevor er in den Zustand 1 übergeht, wo er den Bitinvertierungsprozess umkehrt.
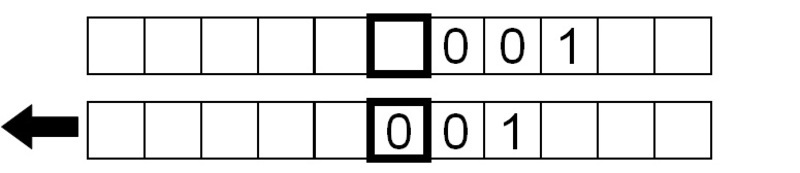
Als Nächstes invertieren wir die Bits wieder, diesmal bewegen wir das Band nach links statt nach rechts.
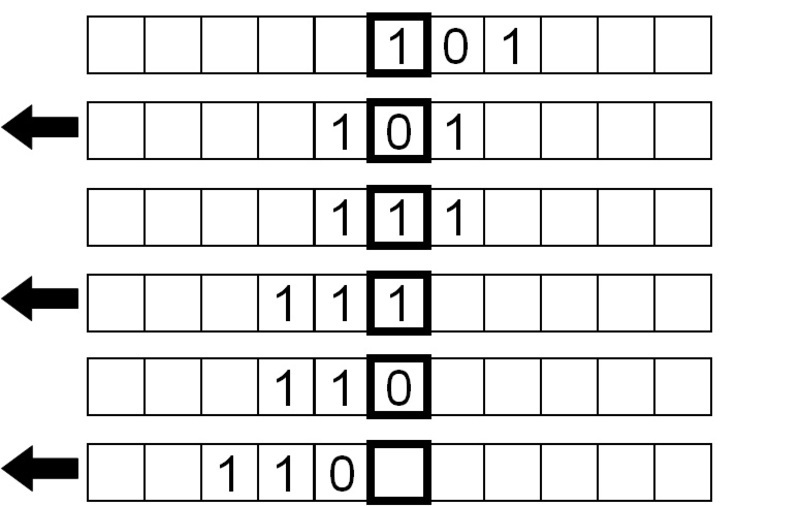
Schließlich wird ein leeres Symbol gelesen, also bewegen wir das Band nach rechts, um wieder an den Anfang zu kommen, und stoppen das Programm.

Mit der Einführung weiterer Zustände in unser Programm können wir die Turing-Maschine anweisen, komplexere Funktionen auszuführen und somit jeden Algorithmus laufen zu lassen, den ein moderner Computer kann.
Im zweiten Teil lernen wir etwas über LEDs, GPIO-Pins, Widerstände und Python, bevor wir mit dem Bau unserer Turing-Maschine beginnen!