12.4 : Techniques de conversion numérique-analogique

Le convertisseur numérique-analogique de base n’est guère plus qu’un amplificateur sommateur pondéré. Chaque bit successif du mot numérique représente un niveau qui est deux fois plus grand que le bit précédent. Si chaque bit est considéré comme un courant ou une tension donnée, les niveaux croissants peuvent être produits en utilisant différents gains dans les entrées de sommation. Un convertisseur à quatre bits simple est illustré à la figure \(\PageIndex{1}\).

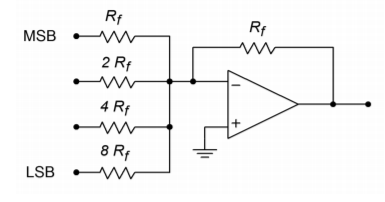
Figure \(\PageIndex{1}\) : Un simple convertisseur 4 bits.

Ce système peut représenter \(2^4\), soit 16, niveaux différents. Chaque entrée est pilotée par un simple niveau logique haut/bas qui représente un 1 ou un 0 pour ce bit particulier. Notez que les résistances d’entrée varient par facteurs de 2. Le gain pour le chemin le plus élevé est de \(R_f/R_f\), ou unité. Cette entrée est utilisée pour le bit le plus significatif du mot d’entrée (MSB). L’entrée suivante présente un gain de \(R_f / (2R_f)\), soit 0,5. La troisième entrée présente un gain de 0,25, et la dernière entrée présente un gain de 0,125. La dernière entrée a le gain le plus faible et est utilisée pour le bit le moins significatif du mot d’entrée (LSB). Si le mot d’entrée avait une résolution plus élevée (c’est-à-dire plus de bits), des canaux supplémentaires seraient ajoutés, chacun ayant la moitié du gain de l’entrée précédente. Pour mieux comprendre le processus de conversion, examinons quelques entrées et sorties représentatives.

Le circuit de la figure \(\PageIndex{1}\) peut être piloté par de simples circuits logiques de type TTL 5 V. 5 V représente un niveau logique haut, tandis que 0 V représente un niveau logique bas. Quel est le niveau de sortie si le mot d’entrée est 0100 ? Comme un niveau logique élevé représente 5 V, 5 V sont appliqués à la deuxième entrée. Toutes les autres entrées reçoivent un bas logique, ou 0 V. La sortie est la somme des signaux d’entrée (n’oubliez pas qu’il s’agit d’un été inverseur, donc la sortie finale doit avoir son signe inversé).

Donc, une valeur de 4 (binaire 100) équivaut à un potentiel de 2,5 V. Si nous augmentons la valeur du mot à 9 (binaire 1001), nous voyons

La sortie minimale se produit au binaire 0000, (0 V) et la maximale au binaire 1111 (-9,375 V). La taille du pas est égale au niveau logique multiplié par le gain minimum ; dans ce cas, c’est 0,625 V. Remarquez que la valeur de sortie peut être trouvée en multipliant simplement la valeur du mot d’entrée par la taille de pas minimale. Il est également important de noter que le signal de sortie est unipolaire (dans cet exemple, toujours négatif).

Une représentation numérique, bien sûr, est constituée d’une séquence de mots, et non d’un seul mot. En réalité, les circuits logiques alimentent constamment l’amplificateur sommateur en nouveaux mots à un rythme prédéterminé. En raison des entrées changeantes, la sortie du convertisseur change également constamment. En utilisant les valeurs calculées précédemment, si le convertisseur reçoit la séquence \(0000, 0100, 1001, 1111,\), la sortie passera de 0 V à -2,5 V, à -5.625 V, jusqu’à une valeur finale de -9,375 V. Cette sortie est représentée graphiquement sur la figure \(\PageIndex{2}\).

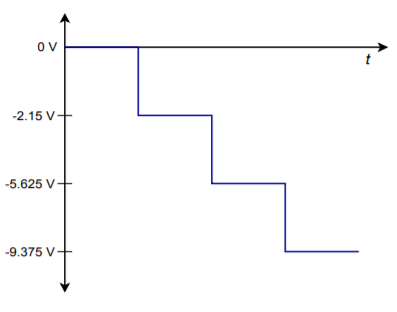
Figure \(\PageIndex{2}\) : Sortie avec quatre mots numériques.

Si cette séquence est répétée à l’infini, on obtient la forme d’onde de la figure \(\PageIndex{3}\). Notez qu’une onde de type » escalier » est créée. Vous pouvez également considérer ceci comme une forme très approximative de fonction de rampe. Une meilleure rampe serait produite si nous utilisions toutes les valeurs disponibles pour la séquence d’entrée, comme dans \(0000, 0001, 0010, 0011, \dots , 1111\). Afin d’éliminer le décalage négatif en courant continu et de rendre le signal bipolaire, il suffit de faire passer le signal par un condensateur de couplage. La fréquence de cette forme d’onde est contrôlée par la vitesse à laquelle les mots sont fournis au convertisseur. Notez qu’en augmentant la résolution et le nombre de mots fournis au convertisseur par cycle, on peut obtenir une approximation très proche de la fonction de rampe idéale. D’ailleurs, en remplaçant les mots d’entrée par d’autres séquences, on peut créer une grande variété de formes d’onde de sortie. C’est le concept qui sous-tend le générateur de fonctions arbitraires numériques. Un générateur de fonctions arbitraires vous permet de créer des formes d’onde autres que les simples sinus/carrés/triangles que l’on trouve sur le générateur de fonctions de laboratoire typique. Nous examinerons de plus près cet équipement de test particulier un peu plus tard.

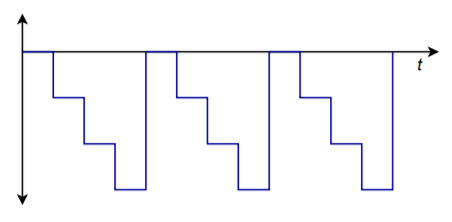
Figure \(\PageIndex{3}\) : Sortie cyclée.

Pour augmenter la résolution, il semble que tout ce que vous devez faire à l’amplificateur sommateur est d’ajouter des canaux supplémentaires avec des résistances de plus en plus grandes. Malheureusement, les tailles des résistances deviennent vite impraticables et une autre approche est nécessaire. Par exemple, pour un système 16 bits, la résistance LSB doit être égale à 65 536 \(R_f\). L’un des problèmes est que le faible courant d’entrée qui en résulte peut être éclipsé par les courants de polarisation et de décalage d’entrée. En outre, une grande précision des composants est nécessaire pour les entrées les plus importantes en termes de résistances d’entrée et de signaux de commande. Les résistances excessivement grandes peuvent également contribuer au bruit supplémentaire. La solution standard à ce problème implique l’utilisation d’un réseau diviseur résistif \(R/2R\).

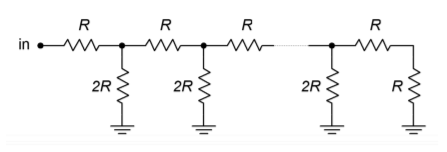
Figure \(\PageIndex{4}\) : Réseau en échelle \(R/2R\)

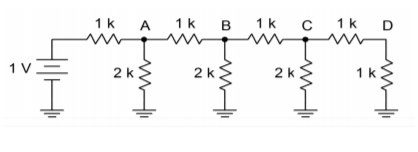
Figure \(\PageIndex{5}\) : Une échelle à 4 étages.

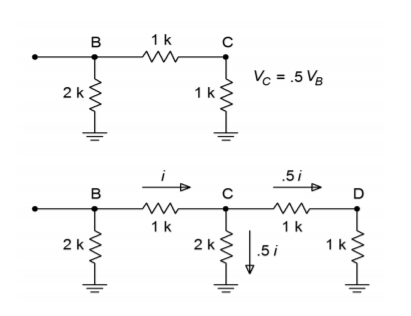
Figure \(\PageIndex{6}\) : Analyse en échelle. a. Circuit équivalent (haut). b. Division du courant (bas).

Si vous regardez la section du circuit équivalent de la figure \(\PageIndex{6}\), vous remarquerez que cette portion ressemble maintenant exactement à la portion finale du réseau original. Autrement dit, chaque fois qu’une section est simplifiée et analysée, le résultat est une réduction de moitié de la tension et du courant. Il est déjà évident que la tension à \(D\) doit être la moitié de la tension à \(C\), qui à son tour, doit être la moitié de la tension à \(B\). Comme vous pouvez maintenant le prouver, il s’ensuit que la tension à \(B\) doit être la moitié de la tension à \(A\). De la même manière, le courant passant par chaque branche de \(2R\) est la moitié du courant précédent. (Pour la division du courant, la section finale n’est pas utilisée pour dériver un courant puisqu’il sera égal à la valeur de l’étape précédente). La division par deux du courant est juste ce qui est nécessaire pour la représentation binaire du mot d’entrée numérique.

L’adaptation du réseau \(R/2R\) au convertisseur DA est relativement facile. Le réseau est alimenté par une source de courant stable, chaque élément \(2R\) alimentant un amplificateur sommateur. En série avec chaque élément \(2R\) se trouve un commutateur à semi-conducteurs, qui définit le niveau logique approprié. Ceci est illustré sur la figure \(\N- PageIndex{7}\N-, avec le réseau effectivement sur le côté. Lorsqu’un niveau logique élevé est présenté à un bit donné, le commutateur est fermé et le courant circule à travers l’élément \(2R\) et dans l’amplificateur opérationnel. Notez que l’extrémité droite de la résistance est effectivement à la masse, car le nœud de sommation de l’amplificateur opérationnel est une masse virtuelle. Si un niveau logique bas est présenté, le commutateur dévie le courant vers la masse, en contournant l’amplificateur opérationnel. De cette façon, les courants pondérés de manière appropriée sont additionnés et utilisés pour produire la tension de sortie.

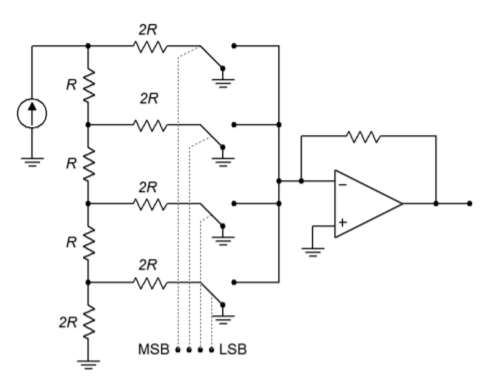
Figure \(\PageIndex{7}\) : Convertisseur avec échelle R/2R.

Cette technique présente plusieurs avantages par rapport à la version plus simple à gain pondéré. Premièrement, toutes les branches sont alimentées par une source de courant commune. De ce fait, il n’est pas nécessaire d’adapter le niveau de sortie. Deuxièmement, seules deux valeurs différentes de résistances sont nécessaires, quel que soit le nombre de bits utilisés, au lieu de l’éventail peu pratique vu précédemment. Il est plus économique de contrôler la tolérance de seulement deux pièces différentes que de 12 ou 16. Notez que de petits courants d’entrée sont encore générés pour les bits les moins significatifs, donc l’attention aux courants de polarisation et de décalage d’entrée reste importante.

12.4.1 : Limites pratiques du convertisseur numérique-analogique

Peut-être que la limite la plus évidente associée au convertisseur DA est sa vitesse. L’amplificateur opérationnel utilisé dans le convertisseur numérique-analogique doit être beaucoup plus rapide que les signaux finaux qu’il est censé produire. Une forme d’onde de sortie donnée peut contenir plusieurs dizaines de points d’échantillonnage individuels par cycle. L’amplificateur opérationnel doit répondre à chaque point d’échantillonnage. Par conséquent, une large bande passante et des taux de balayage élevés sont nécessaires.

Les fiches techniques des DAC intégrés proposent quelques paramètres importants dont vous devez être conscient. Tout d’abord, il y a la vitesse de conversion. Ce chiffre indique combien de temps il faut au DAC pour transformer le mot d’entrée numérique en une tension de sortie analogique stable. Cela définit le débit de données maximum. Viennent ensuite la précision et la résolution. La résolution indique le nombre d’étapes discrètes qui peuvent être produites à la sortie, et est déterminée par le nombre de bits disponibles. Ce n’est pas la même chose que la précision. La précision est en fait composée de plusieurs facteurs différents, notamment l’erreur de décalage, l’erreur et la non-linéarité. L’erreur de décalage est normalement mesurée en appliquant un mot d’entrée entièrement nul, puis en mesurant le signal de sortie. Idéalement, ce signal sera de zéro volt. L’écart par rapport à zéro est considéré comme l’erreur de décalage. Cela a pour effet de rendre tous les niveaux de sortie imprécis par une tension constante. L’erreur de décalage est relativement facile à compenser dans de nombreuses applications en appliquant un décalage égal de polarité opposée. L’erreur de gain est une déviation qui affecte chaque niveau de sortie d’un pourcentage constant. C’est comme si le signal passait par un petit amplificateur ou un atténuateur. Cette erreur peut être compensée en utilisant un amplificateur dont le gain est égal à l’inverse de l’erreur. Les deux gains s’annuleront effectivement. L’effet de l’erreur de décalage et de gain est illustré sur les figures \(\PageIndex{8}\) et \(\PageIndex{9}\).

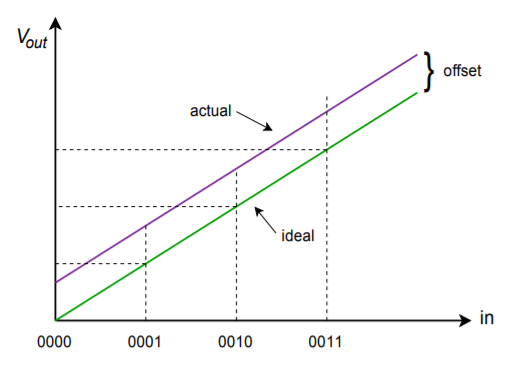
Figure \(\PageIndex{8}\) : Erreur de décalage uniquement.

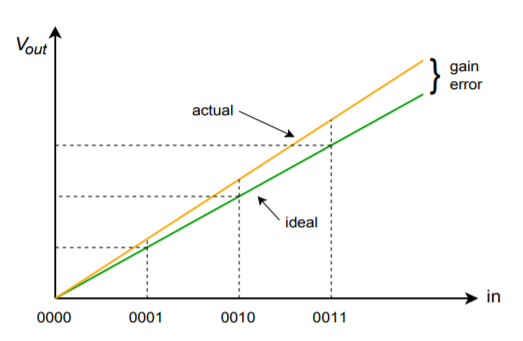
Figure \(\PageIndex{9}\) : Erreur de gain uniquement.

Les erreurs de non-linéarité peuvent être décomposées en deux formes : la non-linéarité intégrale et la non-linéarité différentielle. La non-linéarité intégrale détaille le décalage maximal entre les sorties idéales et les sorties réelles pour toutes les entrées possibles. La non-linéarité différentielle détaille l’écart maximal des sorties par rapport à un LSB causé par deux mots d’entrée adjacents. Si la non-linéarité différentielle est supérieure à \(\pm 1\) LSB, le système peut être non monotone. En d’autres termes, un mot d’entrée numérique plus élevé peut en fait produire une tension de sortie analogique plus faible. Ces deux formes d’erreur sont illustrées sur la Figure \(\PageIndex{10}\). Notez qu’il est possible d’avoir une non-linéarité intégrale élevée tout en ayant une non-linéarité différentielle modeste. C’est le cas sur la figure \(\PageIndex{10b}\).

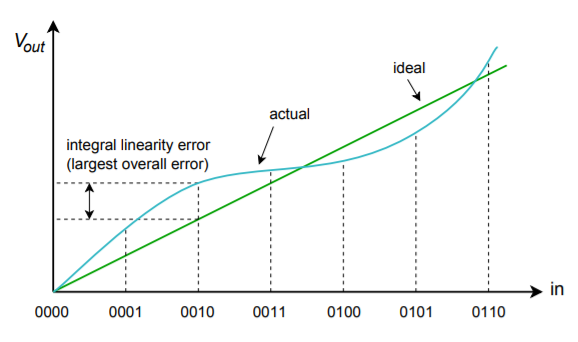
Figure \(\PageIndex{10a}\) : Erreur de linéarité Erreur de linéarité intégrale.

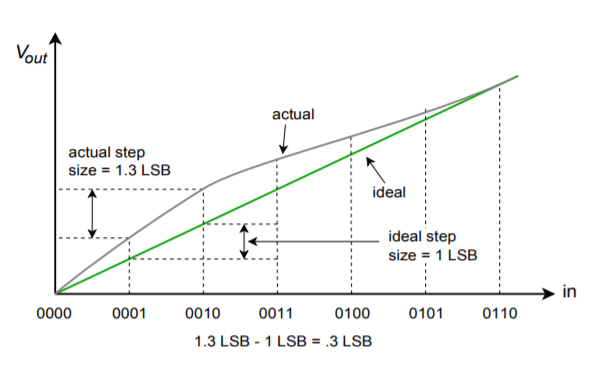
Figure \(\PageIndex{10b}\) : Erreur de linéarité (suite) Erreur de linéarité différentielle (erreur relative-adjacente).

Comme vous pouvez le constater, la précision dépend de facteurs plutôt complexes. Dans un effort pour ramener cela à un seul chiffre, certains fabricants donnent une spécification du nombre effectif de bits. Par exemple, un CNA 16 bits peut être spécifié comme ayant une précision de 14 bits. Cela signifie que les 14 bits les plus significatifs se comportent de manière idéale, mais que les 2 bits les plus bas peuvent être écrasés par des erreurs de linéarité. Une autre spécification que vous verrez parfois est l’absence de codes manquants. Cela signifie que pour chaque augmentation du mot d’entrée, il y aura un changement positif approprié du niveau de sortie.

En pratique, le convertisseur DA standard est utilisé avec un filtre de sortie. Comme vous pouvez le voir sur les figures précédentes, les formes d’onde produites par le CNA contiennent un effet secondaire en escalier. En général, ce n’est pas souhaitable. Les changements brusques du niveau de sortie indiquent la présence de composantes de plus haute fréquence. Toutes les composantes supérieures au taux de Nyquist doivent être filtrées à l’aide d’un filtre passe-bas approprié. Ce filtre est parfois appelé filtre de reconstruction ou de lissage. Dans un système mal conçu, le filtre de reconstruction éliminera certaines des composantes de fréquence intra-bande les plus élevées (c’est-à-dire les composantes immédiatement inférieures à la fréquence de Nyquist). Pour compenser cela, les niveaux logiques sont souvent verrouillés vers le CNA pendant des périodes plus courtes, créant ainsi une apparence plus pointue, plutôt que la forme en escalier. Cet effet est illustré à la figure \(\PageIndex{11}\). Bien que cette forme d’onde en pointe semble moins souhaitable que la forme en escalier, elle crée des niveaux plus élevés pour les composants les plus élevés, et après filtrage, le résultat est une réponse en fréquence globale plus lisse.

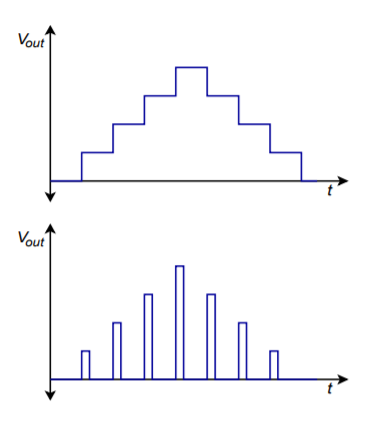
Figure \(\PageIndex{11}\) : Reconstruction de la sortie. a. Loquet à période complète (haut). b. Loquet à période partielle (bas).

Pour augmenter encore la qualité de la forme d’onde de sortie, une technique connue sous le nom de suréchantillonnage est parfois employée. L’idée de base est de créer de nouveaux points d’échantillonnage entre les points existants. Le résultat est un débit de données beaucoup plus dense, qui, espérons-le, donnera des résultats plus exacts après le filtrage. En outre, le débit de données plus élevé peut assouplir les exigences du filtre de reconstruction. Un système typique peut utiliser un suréchantillonnage de quatre fois, ce qui signifie que le taux de données de sortie est quatre fois supérieur à l’original. Par conséquent, pour chaque mot d’entrée, trois nouveaux mots doivent être ajoutés. Cet effet est illustré sur la figure \(\PageIndex{12}\).

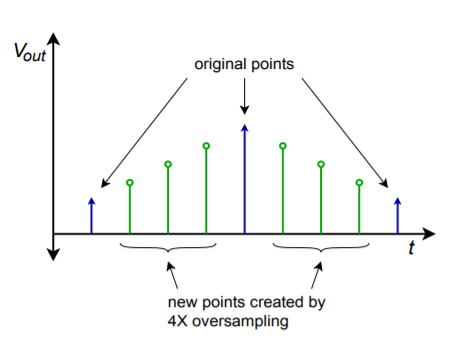
Figure \(\PageIndex{12}\) : Sortie suréchantillonnée.

Il existe plusieurs façons de créer les nouveaux points d’échantillonnage. La manière la plus évidente est via une simple interpolation, mais cela ne permet pas d’obtenir les meilleurs résultats. Une autre technique consiste à initialiser les nouvelles valeurs à zéro, puis à faire passer le flux de données par un filtre numérique passe-bas, qui calcule effectivement les valeurs appropriées. Une extension du principe de suréchantillonnage est la technique delta-sigma. Dans cette technique, des taux de suréchantillonnage très élevés sont utilisés conjointement avec des algorithmes de filtrage numérique spécialisés. Ces algorithmes échangent essentiellement le débit de données plus élevé contre un débit plus lent avec une résolution accrue. La conception et l’analyse des systèmes delta-sigma sont assez avancées et dépassent le cadre de ce texte. Il suffit de dire que ces techniques peuvent augmenter la qualité du signal de sortie et sont largement utilisées dans des applications telles que les lecteurs de CD et de DVD audio de haute qualité.

12.4.2 : Circuits intégrés de convertisseur numérique-analogique

Il existe de nombreuses applications possibles pour les convertisseurs numérique-analogique, et un certain nombre de puces différentes ont évolué pour répondre à des besoins spécifiques. En général, vous pouvez les regrouper en classes spécifiques, telles que la haute vitesse, la haute résolution ou le faible coût. Nous allons examiner trois types représentatifs. Les dispositifs que nous examinerons sont le DAC0832 ; une unité de base de 8 bits, le DAC7545 ; une unité de 12 bits compatible avec les microprocesseurs, et le PCM1716 ; un convertisseur de haute qualité de 24 bits utilisé dans l’industrie audio.

DAC0832

Ce circuit intégré est un convertisseur 8 bits populaire compatible avec les microprocesseurs. Les DAC0830 et DAC0831 sont similaires, mais avec des performances un peu réduites. Il s’agit d’un convertisseur numérique-analogique multiplicateur. En d’autres termes, le signal de sortie est une fonction du mot d’entrée numérique et d’une entrée de référence. Dans certaines applications, l’entrée de référence n’est pas fixe, mais plutôt un signal d’entrée variable. La figure \(\PageIndex{13}\) présente une liste de caractéristiques et le brochage. Les éléments notables sont un temps d’établissement de seulement 1 µs, une faible consommation d’énergie et une linéarité élevée. Le DAC0832 peut être utilisé en mode autonome ou avec un microprocesseur. Les formes d’onde de commutation sont présentées sur la figure \(\PageIndex{14}\).

Figure \(\PageIndex{13}\) : DAC0832. Reproduit avec l’aimable autorisation de Texas Instrutment

Figure \(\PageIndex{14}\) : Formes d’onde de commutation du DAC0832 Reproduit avec l’aimable autorisation de Texas Instrutments

Une application intéressante du DAC0832 se trouve sur la figure \(\PageIndex{15}\). Il s’agit essentiellement d’un filtre à état variable à commande numérique.

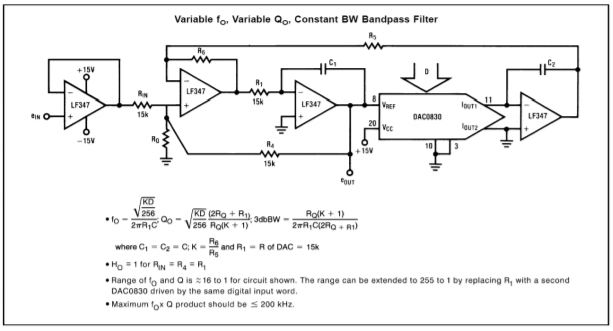
Figure \(\PageIndex{15}\) : Application du filtre à variation d’état DAC0832. Reproduit avec l’aimable autorisation de Texas Instrutments

Notez que le convertisseur remplace la résistance d’entrée du deuxième intégrateur. Normalement, cette résistance serait utilisée pour convertir la tension de sortie du premier intégrateur en un courant d’entrée pour le deuxième intégrateur. Ce travail est maintenant pris en charge par le DAC0832. Le mot d’entrée numérique définit effectivement la conversion tension-courant. Ainsi, un changement dans le mot d’entrée modifie la fréquence d’accord du filtre tout comme un potentiomètre. Comparez ce circuit au filtre commandé en tension basé sur l’OTA du chapitre 11. Conceptuellement, ils sont très similaires.

Figure \(\PageIndex{16}\) : DAC7821. Reproduit avec l’aimable autorisation de Texas Instruments

DAC7821

Le DAC7821 est un convertisseur linéaire 12 bits assez standard et est représenté sur la figure \(\PageIndex{16}\). Ses aspects intéressants sont que c’est un convertisseur multiplicateur et qu’il est compatible avec les microprocesseurs. L’effet multiplicateur provient du fait qu’une référence est utilisée pour piloter le réseau en échelle \(R/2R\). Si la référence est modifiée, la sortie est effectivement remise à l’échelle. Par conséquent, vous pouvez considérer que le signal de sortie est égal à la valeur de référence multipliée par le mot d’entrée numérique. Vous pouvez également considérer cela comme une forme de « contrôle de volume numérique ».

Avec l’inclusion de quelques lignes logiques supplémentaires, le CI est devenu compatible avec les microprocesseurs. Cela signifie que le DAC7821 dispose de lignes de sélection de puce et de lecture/écriture en plus des 12 lignes d’entrée de données. Ceci permet au convertisseur d’être connecté directement au bus de données du microprocesseur. En utilisant des E/S mappées en mémoire, le microprocesseur peut écrire des données dans le convertisseur tout comme il écrit des données en mémoire. Un système à microprocesseur 16 bits peut présenter au convertisseur toutes les données dont il a besoin au cours d’un cycle d’écriture, mais un microprocesseur 8 bits aura besoin de deux cycles d’écriture et d’une forme de verrouillage. Une adresse peut être utilisée pour les 8 bits inférieurs, et une autre adresse pour les 4 bits restants. Un système simplifié est représenté sur la figure \(\PageIndex{17}\) en utilisant un microprocesseur de 8 bits.

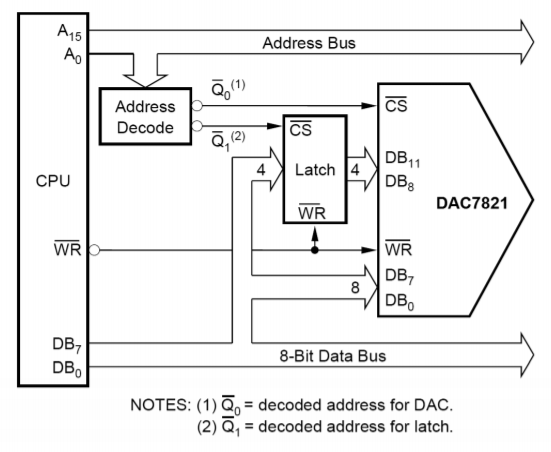
Figure \(\PageIndex{17}\) : Interface entre le microprocesseur et le DAC7821. Reproduit avec l’aimable autorisation de Texas Instruments

PCM5242

Le PCM5242 est un convertisseur stéréo 24 bits conçu spécifiquement pour les applications audio numériques de haute qualité. Il est présenté dans un boîtier VQFN (Very thin Quad Flat No-lead). La figure \(\PageIndex{18a}\) présente un schéma fonctionnel et une liste de caractéristiques. Contrairement aux autres convertisseurs, le PCM5242 dispose d’une entrée de données série et non parallèle. Il intègre ses propres circuits de conversion série et sa propre logique. Cette technique permet de réduire le coût du système. Elle est aussi étonnamment pratique car de nombreux circuits intégrés spécialisés dans le traitement des signaux numériques qui pourraient être utilisés avec le PCM5242 utilisent une sortie de type série. Celle-ci peut être alimentée directement dans le PCM5242 au format 16, 24 ou 32 bits.

Figure \(\PageIndex{18a}\) : PCM5242. Reproduit avec l’aimable autorisation de Texas Instruments

La figure \(\PageIndex{18b}\) présente la fiche technique du PCM5242. Notez que ce dispositif est spécifié avec des fréquences d’échantillonnage de 48 kHz à 192 kHz. La distorsion harmonique totale plus le bruit est généralement de 94 dB sous une sortie pleine échelle lorsqu’il est utilisé avec l’une de ces fréquences d’échantillonnage. En raison de sa haute résolution et de sa plage dynamique de 114 dB, des précautions supplémentaires doivent être prises lors de la mise en place du circuit pour éviter la captation de bourdonnements et les interférences RF.

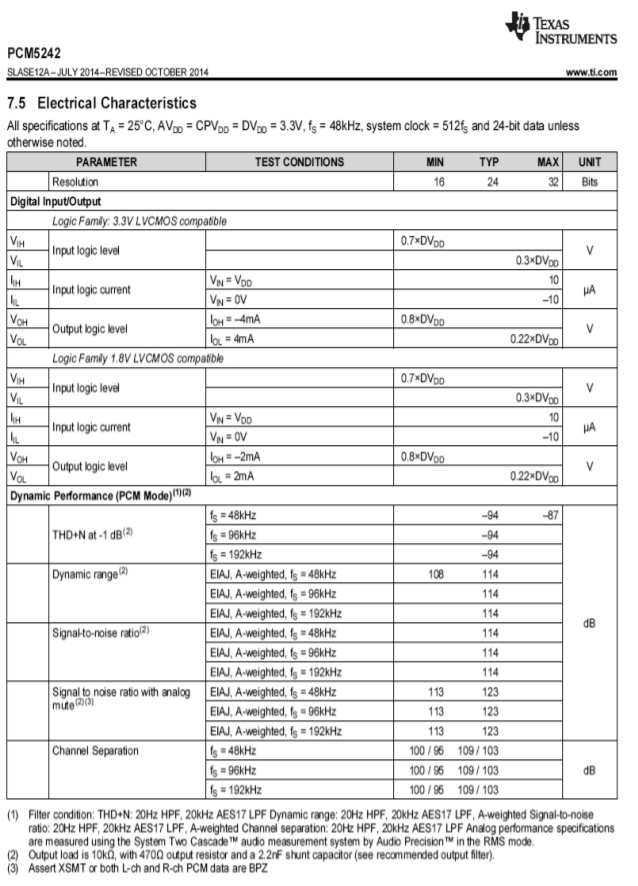
Figure \(\PageIndex{18b}\) : Spécifications du PCM5242. Reproduit avec l’aimable autorisation de Texas Instruments

12.4.3 : Applications des circuits intégrés convertisseurs numérique-analogique

Exemple \(\PageIndex{1}\)

Peut-être que la première chose à laquelle beaucoup de gens pensent lorsqu’ils entendent les termes numérique ou numérisé, est le disque compact audio, ou CD pour faire court. Les lecteurs de CD domestiques sont d’excellents exemples de l’utilisation de circuits DA de précision dans notre vie quotidienne. Les données musicales sont stockées sur le CD avec une résolution de 16 bits et une fréquence d’échantillonnage de 44,1 kHz. Cela produit une fréquence de Nyquist de 22,05 kHz, ce qui est suffisamment élevé pour englober la gamme d’audition de la plupart des humains. La correction d’erreurs et les données auxiliaires sont également stockées sur le disque. Les données sont stockées sur le disque sous la forme de très petits creux, qui sont lus par un laser. Le signal est ensuite converti en une forme logique électronique commune où il est vérifié pour détecter les erreurs et ajusté si nécessaire. Le flux de données est ensuite transmis au convertisseur DA pour la reconstruction audio. Un seul convertisseur peut être multiplexé entre les deux canaux stéréo, ou deux convertisseurs dédiés peuvent être utilisés. Un suréchantillonnage de l’ordre de 2X à 8X est souvent utilisé pour améliorer la qualité du signal. La figure \(\PageIndex{19}\) présente un schéma fonctionnel du système. La partie DAC proprement dite semble presque triviale par rapport à certains éléments plus sophistiqués.

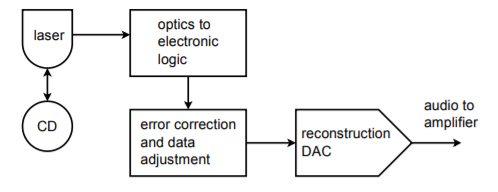
Figure \(\PageIndex{19}\) : Système de lecture de disques compacts audio.

La densité de stockage du CD optique est tout à fait remarquable. Ce petit disque (moins de 5 pouces de diamètre) peut contenir 70 minutes de musique. En ignorant les données auxiliaires, nous pouvons rapidement calculer le stockage total. Nous avons deux canaux de données de 16 bits, soit 32 bits (4 octets) par point d’échantillonnage. Il y a 44 100 échantillons par seconde pendant 70 minutes, ce qui donne 185,22 mégaéchantillons. Le stockage total des données est de 5,927 gigabits, soit 741 mégaoctets.

Exemple \(\PageIndex{2}\)

Comme nous l’avons déjà mentionné, il est possible de connecter des DACs directement à des systèmes à microprocesseur. De plus, le microprocesseur peut écrire dans le DAC sans plus d’effort que pour écrire dans un emplacement mémoire. Le microprocesseur peut écrire n’importe quelle série de mots de données que nous souhaitons sur le DAC et peut répéter une séquence pratiquement à l’infini. Avec cette capacité, nous pouvons créer un générateur de formes d’onde arbitraires. Au lieu d’être enfermé dans un ensemble de formes d’ondes prédéfinies comme sur les générateurs de fonctions ordinaires, ce système permet toutes sortes de formes d’ondes. La précision et la flexibilité du système dépendront de sa vitesse et de la résolution du DAC disponible.

L’idée de base est celle de la consultation de tables. Par exemple, disons que nous avons un système de 16 bits. Nous allons créer une table de valeurs de données pour un cycle de la forme d’onde de sortie. Pour des raisons pratiques, la taille de la table peut être une puissance de 2, par exemple 256. En d’autres termes, un seul cycle de sortie sera découpé en 256 morceaux de temps discrets. Il est donc évident que le convertisseur doit être quelques centaines de fois plus rapide que la plus haute fondamentale que nous souhaitons produire. En augmentant ou en diminuant le débit de données de sortie, nous pouvons modifier la fréquence de la fondamentale de sortie. C’est ce qu’on appelle une technique de fréquence d’échantillonnage variable. Il est également possible de modifier la fréquence du fondamental avec une technique à taux fixe (cette technique est un peu plus complexe, mais présente certains avantages). La figure \(\PageIndex{20}\) présente un organigramme de sortie.

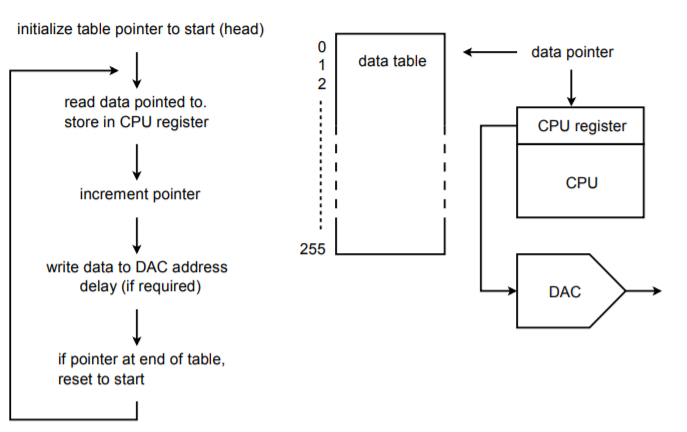
Figure \(\PageIndex{20}\) : Générateur de formes d’onde arbitraires.

Lors de l’initialisation, un pointeur d’adresse est défini sur l’adresse de départ de la table de données. L’unité centrale lit les données de la table via le pointeur. Le pointeur est incrémenté de sorte qu’il pointe maintenant sur l’élément suivant de la table. (Certains processeurs proposent un mode d’adressage post-incrément afin que les deux étapes puissent être réalisées en une seule instruction). Ensuite, le CPU écrit les données à l’adresse spéciale du DAC. À ce stade, une certaine forme de retard logiciel/matériel est invoquée pour fixer le débit de données de sortie. Après le délai, l’unité centrale lit l’élément de données suivant via le pointeur et continue comme lors de la première exécution. Une fois le 256ème élément envoyé, le pointeur est remis au début de la table et le processus continue. De cette façon, la table peut être considérée comme circulaire, ou sans fin. Si le logiciel du système est écrit dans un langage de niveau supérieur, le tableau de pointeurs/données peut être implémenté comme un simple tableau où l’index du tableau est défini par un compteur. Mais cela ne sera pas aussi efficace qu’une approche directe au niveau de l’assemblage.

La vraie beauté de ce système est que la table de données peut contenir pratiquement n’importe quelle séquence de données. Les données pourraient représenter un sinus, une impulsion, un triangle ou toute autre fonction standard. Plus important encore, les données pourraient représenter une onde sinusoïdale avec un transitoire de bruit intégré, ou un signal contenant une composante de ronflement tout aussi facilement. Ces données peuvent provenir de trois sources de base. Premièrement, la table de données peut être remplie par calcul direct si l’équation du domaine temporel de la fonction désirée est connue. Ensuite, les données peuvent être fabriquées par l’utilisateur par le biais d’une certaine forme d’interaction avec un ordinateur, peut-être avec une souris ou un bloc-notes. Enfin, les données peuvent être dérivées d’un signal du monde réel. C’est-à-dire qu’un convertisseur analogique-numérique peut être utilisé pour enregistrer le signal sous forme numérique. Les données peuvent ensuite être chargées dans le tableau et lues de manière répétée. Le générateur de formes d’onde arbitraires permet à son utilisateur de tester des circuits et des systèmes avec une gamme de formes d’onde qu’il serait impossible ou peu pratique de générer autrement.

Exemple \(\PageIndex{3}\)

Sous le contrôle d’un ordinateur, les convertisseurs DA peuvent être utilisés dans le cadre d’un système d’équipement de test automatisé. Afin de caractériser complètement un produit électronique, un certain nombre de tests individuels doivent être effectués. La mise en place de chaque test individuel peut prendre un certain temps et est sujette à des erreurs de la part de l’opérateur. L’automatisation de cette procédure peut améliorer la répétabilité et réduire la durée des tests. Il existe de nombreuses façons d’automatiser ce processus. Nous allons examiner une approche.

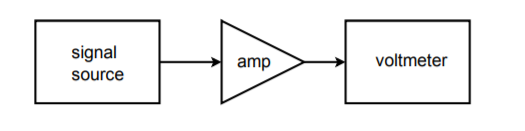
Figure \(\PageIndex{21}\) : Configuration de test simple.

Supposons que nous souhaitons effectuer des mesures de réponse en fréquence pour un amplificateur à 20 fréquences différentes. Un système de test de circuit approprié pour ce travail est illustré sur la figure \(\PageIndex{21}\). Pour effectuer ce test manuellement, il faut 20 réglages distincts du signal source et 20 lectures de sortie correspondantes. Cela peut s’avérer assez fastidieux si de nombreuses unités doivent être testées. Il serait très pratique de pouvoir modifier automatiquement la fréquence de la source en fonction de valeurs prédéfinies. Cela n’est pas particulièrement difficile. La plupart des sources modernes ont des entrées de tension de commande qui peuvent être utilisées pour régler la fréquence. La tension de commande requise peut être créée et réglée avec précision à l’aide d’un ordinateur et d’un convertisseur DA. L’ordinateur peut être programmé pour envoyer des mots numériques spécifiques au convertisseur numérique-analogique, qui alimente à son tour l’entrée de commande de la source de signaux. En d’autres termes, le mot de données règle directement la fréquence de la source du signal. L’ordinateur peut être programmé pour envoyer pratiquement n’importe quelle séquence de mots de données à n’importe quel rythme, et ce, sans intervention de l’opérateur. Tout ce que l’opérateur doit faire, c’est lancer le processus. La répétabilité des tests est très élevée avec un tel système. Un schéma fonctionnel de ce système est présenté sur la figure \(\PageIndex{22}\).

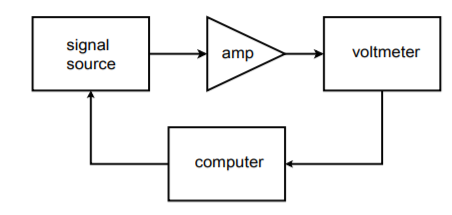
Figure \(\PageIndex{22}\) : Configuration de test automatisé.

Pour enregistrer les données, le voltmètre peut être connecté à un enregistreur à bande, ou mieux encore, renvoyé à l’ordinateur. Les données peuvent être envoyées à l’ordinateur sous forme numérique si le voltmètre est de conception assez avancée, ou, avec l’inclusion d’un convertisseur analogique-numérique, le signal de sortie peut être directement échantillonné et manipulé par l’ordinateur. Dans les deux cas, des fichiers de données peuvent être créés pour chaque unité testée et stockés pour une utilisation ultérieure. De plus, une analyse statistique pratique peut être effectuée rapidement à la fin d’un lot de tests. Notez que, comme le convertisseur DA ne génère qu’un signal de commande, une très haute résolution et une faible distorsion ne sont normalement pas nécessaires. Si un convertisseur haute résolution est utilisé, il est possible de créer les signaux de test dans l’ordinateur (comme dans le générateur de fonctions arbitraires), et de se passer de la source de signaux.

Le système de test automatisé n’est qu’une application possible du contrôle des instruments. Un autre exemple intéressant concerne la génération de « spectacles lumineux » au laser. Le schéma fonctionnel d’un système simplifié est illustré à la figure \(\PageIndex{23}\). Afin de créer les motifs complexes vus par le public, un faisceau laser rebondit sur de minuscules miroirs mobiles. Les miroirs peuvent être montés sur un objet aussi simple qu’un galvanomètre. Le galvanomètre est alimenté par un DAC. Le motif du faisceau laser dépend de la façon dont le galvanomètre déplace le miroir, qui est à son tour contrôlé par les mots de données transmis au CNA. En pratique, plusieurs miroirs peuvent être utilisés pour dévier le faisceau selon trois axes.

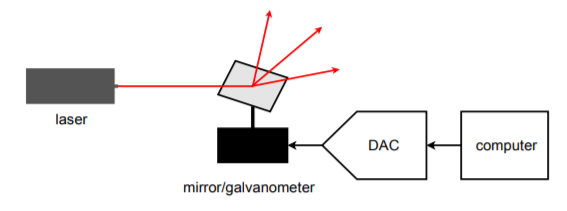
Figure \(\PageIndex{23}\) : Éclairage commandé par ordinateur.

Les convertisseurs ADA peuvent être utilisés pour régler tout appareil doté d’une entrée de type tension de commande. De même, ils peuvent être utilisés pour contrôler des dispositifs électromécaniques qui répondent à une tension appliquée. Leur véritable avantage est la répétabilité et la flexibilité qu’ils offrent.