Calcul du volume
Cette page explique comment calculer le volume des objets solides, c’est-à-dire la quantité que vous pourriez faire entrer dans un objet si, par exemple, vous le remplissiez d’un liquide.
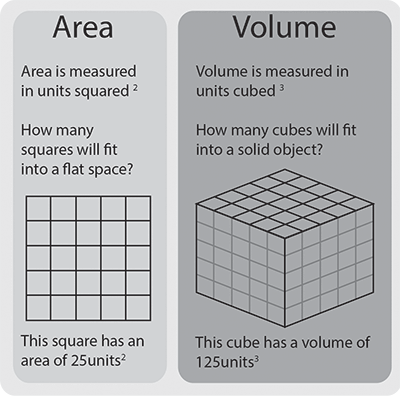
L’aire est la mesure de l’espace qu’il y a dans un objet bidimensionnel (voir notre page : Calculer l’aire pour en savoir plus).
Le volume est la mesure de l’espace qu’il y a dans un objet tridimensionnel. Notre page sur les formes tridimensionnelles explique les bases de ces formes.
Dans le monde réel, le calcul du volume n’est probablement pas quelque chose que vous utiliserez aussi souvent que le calcul de l’aire.
Cependant, il peut toujours être important. Savoir calculer le volume vous permettra, par exemple, de déterminer l’espace d’emballage dont vous disposez lors d’un déménagement, l’espace de bureau dont vous avez besoin ou la quantité de confiture que vous pouvez faire entrer dans un pot.
Cela peut également être utile pour comprendre ce que les médias veulent dire lorsqu’ils parlent de la capacité d’un barrage ou du débit d’une rivière.
Une note sur les unités
L’aire est exprimée en unités carrées, car il s’agit de deux mesures multipliées ensemble.
Le volume est exprimé en unités cubiques, car il s’agit de la somme de trois mesures (longueur, largeur et profondeur) multipliées ensemble. Les unités cubiques comprennent les cm3, les m3 et les pieds cubes.
Attention !
Le volume peut également être exprimé en capacité liquide.
Système métrique
Dans le système métrique, la capacité liquide est mesurée en litres, ce qui est directement comparable à la mesure cubique, puisque 1ml = 1cm3. 1 litre = 1 000 ml = 1 000cm3.
Système impérial/anglais
Dans le système impérial/anglais, les mesures équivalentes sont les onces liquides, les pintes, les quarts et les gallons, qui ne se traduisent pas facilement en pieds cubes. Il est donc préférable de s’en tenir aux unités de volume des liquides ou des solides.
Pour en savoir plus, consultez notre page sur les systèmes de mesure
Formules de base pour le calcul du volume
Volume des solides à base de rectangle

Alors que la formule de base pour la surface d’une forme rectangulaire est longueur × largeur, la formule de base pour le volume est longueur × largeur × hauteur.
La façon dont vous vous référez aux différentes dimensions ne change pas le calcul : vous pouvez, par exemple, utiliser » profondeur » au lieu de » hauteur « . L’important est que les trois dimensions soient multipliées ensemble. Vous pouvez multiplier dans l’ordre que vous voulez car cela ne changera pas la réponse (voir notre page sur la multiplication pour en savoir plus).
Une boîte ayant pour dimensions 15 cm de largeur, 25 cm de longueur et 5 cm de hauteur a un volume de :
15 × 25 × 5 = 1875cm3
Volume des prismes et des cylindres
Cette formule de base peut être étendue au volume des cylindres et des prismes également. Au lieu d’une extrémité rectangulaire, vous avez simplement une autre forme : un cercle pour les cylindres, un triangle, un hexagone ou, en fait, tout autre polygone pour un prisme.
Effectivement, pour les cylindres et les prismes, le volume est l’aire d’un côté multiplié par la profondeur ou la hauteur de la forme.
La formule de base pour le volume des prismes et des cylindres est donc :
Aire de la forme d’extrémité × la hauteur/profondeur du prisme/cylindre.
Volume des cônes et des pyramides
Le même principe que ci-dessus (largeur × longueur × hauteur) vaut pour le calcul du volume d’un cône ou d’une pyramide, sauf que, comme ils arrivent à un point, le volume n’est qu’une proportion du total qu’il serait s’ils continuaient à avoir la même forme tout du long.
Le volume d’un cône ou d’une pyramide est exactement le tiers de ce qu’il serait pour une boîte ou un cylindre ayant la même base.
La formule est donc :
Aire de la base ou de la forme terminale × la hauteur du cône/pyramide × 1/3
Retournez à notre page Calculer l’aire si vous ne vous souvenez plus comment calculer l’aire d’un cercle ou d’un triangle.
Par exemple, pour calculer le volume d’un cône de 5 cm de rayon et de 10 cm de hauteur :
L’aire d’un cercle = πr2 (où π (pi) vaut environ 3,14 et r est le rayon du cercle).
Dans cet exemple, l’aire de la base (cercle) = πr2 = 3,14 × 5 × 5 = 78,5cm2.
78,5 × 10 = 785
785 × 1/3 = 261,6667cm3

Volume d’une sphère
Comme pour un cercle, vous avez besoin de π (pi) pour calculer le volume d’une sphère.
La formule est 4/3 × π × rayon3.
Vous vous demandez peut-être comment vous pourriez calculer le rayon d’une balle. À moins de lui planter une aiguille à tricoter (efficace, mais terminale pour la balle !), il existe un moyen plus simple.
Vous pouvez mesurer directement la distance autour du point le plus large de la sphère, par exemple avec un mètre ruban. Ce cercle est la circonférence et a le même rayon que la sphère elle-même.
La circonférence d’un cercle se calcule comme 2 x π x rayon.
Pour calculer le rayon à partir de la circonférence vous :
Divisez la circonférence par (2 x π).
Exemples travaillés : Calcul du volume
Exemple 1

Calculez le volume d’un cylindre d’une longueur de 20cm, et dont l’extrémité circulaire a un rayon de 2,5cm.
D’abord, calculez l’aire d’une des extrémités circulaires du cylindre.
L’aire d’un cercle est πr2 (π × rayon × rayon). π (pi) vaut environ 3,14.
L’aire d’une extrémité est donc :
3,14 x 2,5 x 2,5 = 19,63cm2
Le volume est l’aire d’une extrémité multipliée par la longueur, et est donc :
19.63cm2 x 20cm = 392,70cm3

Exemple 2
Qu’est-ce qui est le plus grand en volume, une sphère de rayon 2cm ou une pyramide de base carrée de 2,5cm et de hauteur 10cm ?
D’abord, calculez le volume de la sphère.
Le volume d’une sphère est égal à 4/3 × π × rayon3.
Le volume de la sphère est donc :
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51cm3
Puis calculez le volume de la pyramide.
Le volume d’une pyramide est égal à 1/3 × aire de la base × hauteur.
Aire de la base = longueur × largeur = 2,5cm × 2,5cm = 6,25cm2
Le volume est donc de 1/3 x 6,25 × 10 = 20,83cm3
La sphère est donc plus grande en volume que la pyramide.
Calcul du volume des solides irréguliers
De même que vous pouvez calculer l’aire des formes bidimensionnelles irrégulières en les décomposant en formes régulières, vous pouvez faire de même pour calculer le volume des solides irréguliers. Il suffit de diviser le solide en parties plus petites jusqu’à ce que vous n’atteigniez que des solides avec lesquels vous pouvez travailler facilement.
Exemple travaillé
Calculez le volume d’un cylindre d’eau d’une hauteur totale de 1m, d’un diamètre de 40cm, et dont la section supérieure est semi-sphérique.

Vous divisez d’abord la forme en deux sections, un cylindre et une demi-sphère (une demi-sphère).
Le volume d’une sphère est 4/3 × π × rayon3. Dans cet exemple, le rayon est de 20 cm (la moitié du diamètre). Comme le sommet est semi-sphérique, son volume sera la moitié de celui d’une sphère complète. Le volume de cette section de la forme est donc :
0,5 × 4/3 × π × 203 = 16 755,16cm3
Le volume d’un cylindre est la surface de la base × la hauteur. Ici, la hauteur du cylindre est la hauteur totale moins le rayon de la sphère, soit 1m – 20cm = 80cm. L’aire de la base est πr2.
Le volume de la section cylindrique de cette forme est donc :
80 × π × 20 × 20 = 100 530,96cm3
Le volume total de ce récipient d’eau est donc :
100 530,96 + 16 755,16 = 117 286,12cm3.
C’est un nombre assez important, vous préférerez peut-être le convertir en 117,19 litres en le divisant par 1 000 (puisqu’il y a 1000cm3 dans un litre). Cependant, il est tout à fait correct de l’exprimer en cm3 puisque le problème ne demande pas que la réponse soit exprimée sous une forme particulière.
En conclusion…
En utilisant ces principes, si nécessaire, vous devriez maintenant être en mesure de calculer le volume de presque tout ce qui vous entoure, qu’il s’agisse d’une caisse d’emballage, d’une pièce ou d’un cylindre d’eau.