Département des sciences et technologies informatiques
Qu’est-ce qu’une machine de Turing ?
Une machine de Turing est une machine hypothétique pensée par le mathématicien Alan Turing en 1936. Malgré sa simplicité, cette machine peut simuler N’IMPORTE QUEL algorithme informatique, aussi compliqué soit-il !

Vous trouverez ci-dessus une représentation très simple d’une machine de Turing. Elle consiste en une bande infiniment longue qui agit comme la mémoire d’un ordinateur typique, ou toute autre forme de stockage de données. Les cases de la bande sont généralement vierges au départ et peuvent être écrites avec des symboles. Dans ce cas, la machine ne peut traiter que les symboles 0 et 1 et » » (blanc), et on dit donc que c’est une machine de Turing à 3 symboles.
À tout moment, la machine possède une tête qui est positionnée sur l’un des carrés de la bande. Avec cette tête, la machine peut effectuer trois opérations très basiques:
- Lire le symbole sur le carré sous la tête.
- Modifier le symbole en écrivant un nouveau symbole ou en l’effaçant.
- Déplacer la bande à gauche ou à droite d’un carré de sorte que la machine puisse lire et modifier le symbole sur un carré voisin.
Une démonstration simple
A titre d’exemple trivial pour démontrer ces opérations, essayons d’imprimer les symboles « 1 1 0 » sur une bande initialement vierge :

Premièrement, nous écrivons un 1 sur le carré sous la tête :

Puis, nous déplaçons la bande vers la gauche d’un carré :

Maintenant, on écrit un 1 sur le nouveau carré sous la tête :

Nous déplaçons ensuite à nouveau le ruban vers la gauche d’un carré :

Enfin, écrivez un 0 et c’est tout !

Un programme simple
Avec les symboles « 1 1 0 » imprimés sur la bande, essayons de convertir les 1 en 0 et vice versa. Cela s’appelle l’inversion de bits, puisque les 1 et les 0 sont des bits en binaire. Pour ce faire, il suffit de transmettre les instructions suivantes à la machine de Turing, en utilisant les capacités de lecture de la machine pour décider elle-même des opérations suivantes. Ces instructions constituent un programme simple.
| Symbole lu | Instruction d’écriture | Instruction de déplacement | Non | None | None | 0 | Ecriture 1 | Déplacement de la bande vers la droite | 1 | Écriture 0 | Déplacement de la bande vers la droite |
|---|
La machine va d’abord lire le symbole sous la tête, écrire un nouveau symbole en conséquence, puis déplacer la bande à gauche ou à droite selon les instructions, avant de répéter à nouveau la séquence lecture-écriture-déplacement.
Voyons ce que ce programme fait à notre bande à partir du point final précédent des instructions:

Le symbole actuel sous la tête est 0, nous écrivons donc un 1 et déplaçons la bande vers la droite d’une case.
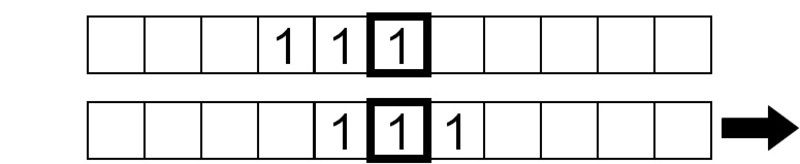
Le symbole en cours de lecture est maintenant 1, donc on écrit un 0 et on déplace la bande vers la droite d’une case:
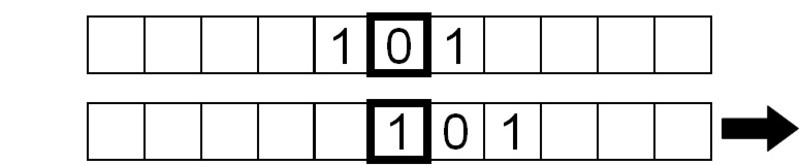
De même, le symbole lu est un 1, donc on répète les mêmes instructions.
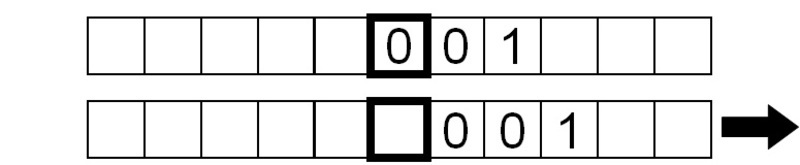
Enfin, un symbole » blanc » est lu, donc la machine ne fait rien à part lire le symbole blanc en continu puisque nous lui avons demandé de répéter la séquence lecture-écriture-déplacement sans s’arrêter.
En fait, le programme est incomplet. Comment la machine répète-t-elle la séquence à l’infini, et comment cesse-t-elle d’exécuter le programme ? Le programme le lui indique grâce au concept d’état de la machine.
L’état de la machine
Pour compléter le programme, il faut tenir compte des changements d’état pendant l’exécution du programme sur la machine. Les modifications suivantes, marquées en italique, doivent être ajoutées à notre tableau qui peut maintenant être appelé tableau d’états :
| Etat | Symbole lu | Instruction d’écriture | Instruction de déplacement | État suivant |
|---|---|---|---|---|
| État 0 | Vide | None | None | État d’arrêt | 0 | Écriture 1 | Déplacement de la bande vers la droite | État 0 | 1 | Écriture 0 | Déplacement de la bande vers la droite | État 0 |
Nous attribuons l’ensemble des instructions précédentes à un état de la machine, afin que la machine exécute ces instructions lorsqu’elle se trouve dans l’état spécifié.
Après chaque instruction, nous spécifions également un état vers lequel la machine effectue une transition. Dans l’exemple, la machine est redirigée vers son état d’origine, l’état 0, pour répéter la séquence lecture-écriture-nouveau, sauf si un symbole vide est lu. Lorsque la machine lit un symbole vide, elle est dirigée vers un état d’arrêt et le programme se termine.
Machines à états finis
Même si cela semble idiot de le faire, ajoutons maintenant un état supplémentaire à notre programme qui renvoie les bits « 1 1 0 » déjà inversés de « 0 0 1 » à « 1 1 0 ». Voici le tableau mis à jour, avec les changements indiqués en italique. La machine de Turing se comporte maintenant comme une machine à états finis à deux états – on parle alors de machines de Turing à trois symboles et à deux états.
| État | Symbole lecture | Écriture instruction | Instruction de déplacement | État suivant |
|---|---|---|---|---|
| État 0 | Vierge | Écriture blanc | Déplacement de la bande vers la gauche | État 1 |
| 0 | Écriture 1 | Déplacement de la bande vers la droite | État 1 | |
| Écriture 0 | Déplacement de la bande vers la droite | État 0 | ||
| État 1 | Blank | Écriture à blanc | Déplacement de la bande vers la droite | État d’arrêt | 0 | Écriture. 1 | Déplacement de la bande vers la gauche | État 1 |
| 1 | Écriture 0 | Déplacement de la bande vers la gauche | État 1 |
Pour l’instruction d’écriture, « Aucun » a été remplacé par « Écriture à blanc » par souci d’uniformité (afin de ne faire référence qu’aux symboles de la machine), et il faut noter qu’ils sont équivalents.
Au lieu d’un tableau d’états, on peut aussi représenter le programme par un diagramme d’états :
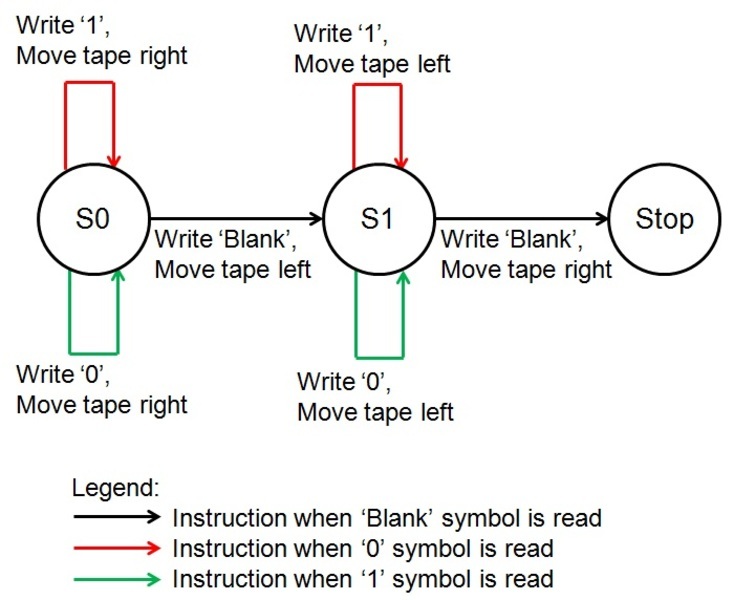
À partir de l’endroit où se trouvait le programme précédemment, au lieu de ne rien faire et de s’arrêter après que la machine a rencontré un symbole vide, on lui ordonne de déplacer la bande vers la gauche avant de passer à l’état 1 où elle inverse le processus d’inversion des bits.
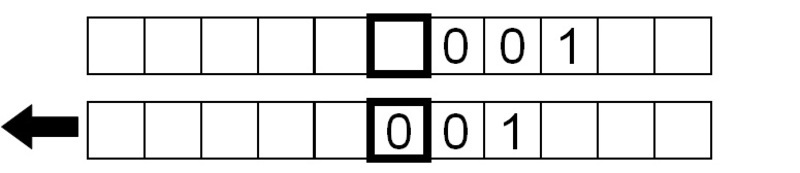
Puis, nous inversons à nouveau les bits, cette fois en déplaçant la bande vers la gauche au lieu de la droite.
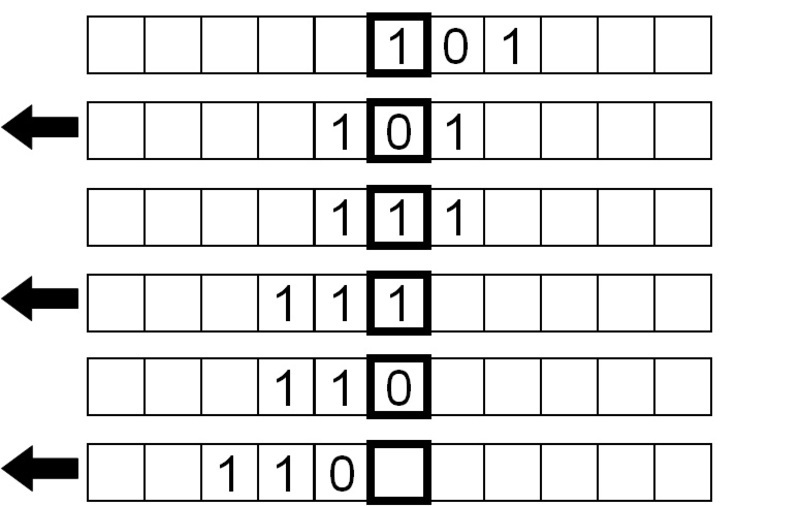
Enfin, un symbole vide est lu, nous déplaçons donc la bande vers la droite pour revenir à notre point de départ, et nous arrêtons le programme.

Avec l’introduction de plus d’états dans notre programme, nous pouvons ordonner à la machine de Turing d’exécuter des fonctions plus complexes et donc d’exécuter n’importe quel algorithme qu’un ordinateur moderne peut exécuter.
Dans la section deux, apprenons à connaître les LED, les broches GPIO, les résistances et python, avant de nous lancer dans la construction de notre machine de Turing !
.