Quelle est la différence entre PNP et NPN ?

Cet article est paru dans Microwaves & RF et a été publié ici avec autorisation.

Ce que vous apprendrez :

• Le débit maximal d’un canal en fonction du débit de symboles et de la bande passante.
• Le débit maximal d’un canal en fonction de l’interférence du bruit.
• Comment les considérations de débit remontent jusqu’à l’utilisateur.

C’est une chose très facile et normale de se concentrer sur les principales caractéristiques des principaux composants d’un système ou d’une liaison de communication, et de considérer les autres éléments et questions comme périphériques et pas si importants. Que cela se soit produit de manière surprenante avec les liaisons de communication par satellite, en particulier les liaisons mobiles à distance, est la raison de cette missive.

Voici une situation hypothétique. Vous êtes un soldat. Vous êtes déployé dans une zone montagneuse du Moyen-Orient, vous transportez un vieux terminal satellite Intelsat pour un accès immédiat au quartier général, et le quartier général a loué un transpondeur de 72 MHz pour votre usage exclusif.

Un endroit agréable et sûr est une grotte, alors vous tendez un câble de communication vers le terminal satellite à l’entrée de la grotte et vous vous asseyez pour vérifier votre station de travail qui est connectée au terminal avec un modem à déplacement de phase en quadrature (QPSK). La connexion est bonne, mais la communication est mauvaise. La compagnie de satellite vous garantit 72 Mb/s (1 bit par Hz), mais vous obtenez à peine moins de 35 Mb/s. Auriez-vous dû vous procurer un terminal plus récent ? Auriez-vous dû utiliser un autre système ?

Débits maximaux Nyquist

La réponse réelle est ce que Harry Nyquist et Claude Shannon ont dit à propos des débits maximaux sur chaque canal, y compris ce câble de communication. Harry Nyquist a noté, comme cela a été minutieusement documenté1, que le nombre maximal de bits que vous pouvez obtenir par un canal (bruit non pris en compte) est :

Max R = 2 H Log2V

où H est la largeur de bande du canal et V est le nombre de symboles discrets (la modulation par déplacement de phase binaire, ou BPSK, est de 2, la QPSK est de 4, etc.)

Si vous n’êtes pas familier avec le log2, ce n’est pas difficile une fois que vous vous y êtes habitué. Le log2V est simplement l’exposant auquel il faut élever 2 pour égaler V. Ainsi, si V est BPSK (2), alors l’expression log2V est simplement 1, puisque 21 est en fait 2 ; et si V est QPSK (4), alors l’expression log2V est 2 puisque 22 est en fait 4, et ainsi de suite.

Si vous utilisez un câble Cat 3 de 10 MHz, alors le débit maximal de données DANS le terminal satellite est de 20 Mb/s en BPSK, 40 Mb/s en QPSK et 30 Mb/s en 8PSK, en fonction des relations log2. La figure 1 montre le nombre d’états et leur logarithme par rapport à l’équivalent en base 2. Par conséquent, la limite de Nyquist, en utilisant le modem QPSK, est de 40 Mb/s.

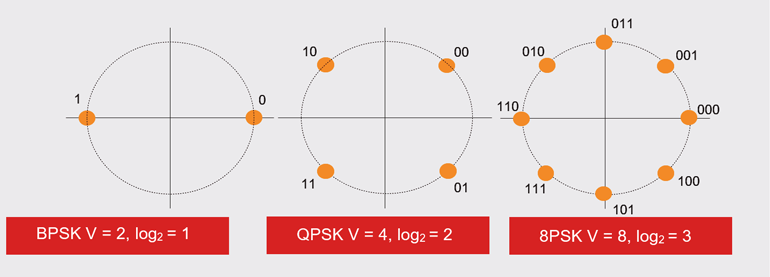1. La MDPB, ayant deux états, a une valeur log2 de 1 ; la MDPQ, ayant quatre états, a une valeur log2 de 2 ; et ainsi de suite.

Débits maximums de Shannon

Bien, Harry Nyquist travaillait la question des débits maximums sans tenir compte du bruit alors que Claude Shannon la travaillait strictement en fonction du bruit. Son équation2 dit :

Max R = H log2 (1 + SNR)

où H est à nouveau la largeur de bande du canal et le SNR est la puissance du signal divisée par la puissance du bruit, généralement donnée en dB. Supposons que le SNR sur ce même câble Cat 3 soit d’environ 30 dB ou 1 000 en chiffres bruts (le SNR doit être reconverti en sa valeur rationnelle pour calculer une exponentielle). Puisque nous avons augmenté l’échelle des exponentielles de 2, nous pouvons continuer à le faire. La figure 2 illustre cette progression.

2. Un nombre, indiqué sur la ligne supérieure, a une valeur exponentielle, indiquée sur la ligne inférieure, et démontre la signification de la température de bruit du système par rapport à un débit de canal.

Si nous arrondissons un peu par souci de simplicité, 1 001 est plus proche de 1 024 que tout autre incrément et 2 élevé à la 10e puissance vous donne une valeur bien plus proche que tout autre exposant. Assis au fond de votre grotte avec un câble Cat 3 d’une largeur de bande de 10 MHz, Claude Shannon dit que vous devriez obtenir un débit de données de 10 x 106 (10) = 100 Mb/s.

Si Claude Shannon dit que vous pouvez obtenir un débit de données maximum dans le terminal de communication par satellite de 100 Mb/s et que Harry Nyquist dit que vous ne pouvez obtenir que 40 Mb/s vers et depuis votre poste de travail équipé de QPSK, qui a raison ?

Regardons une autre analogie. L’université de Notre Dame a une équipe de football limitée sur le plan académique mais relativement bonne. En revanche, elle possède une excellente fanfare, car les musiciens exceptionnels sont fréquemment des lycéens exceptionnels. Pour entrer sur le terrain, la fanfare doit franchir deux arches, l’une autorisant 15 membres de front et l’autre 10. Combien de membres de front la fanfare doit-elle former ? Eh bien, de la même manière, Nyquist et Shannon ne sont pas en compétition. Ce sont juste deux portes différentes avec deux contraintes différentes.

Ce n’est pas seulement le système majeur. C’est les go-intas et les go-outas jusqu’aux mains qui tapent sur le clavier. Et les articles originaux publiés par le physicien Nyquist3 et le mathématicien/ingénieur Shannon4 ont encore quelque chose à nous dire.

1. Un exemple de l’équation peut être trouvé dans n’importe quelle édition de Data and Computer Communications de William Stallings répertorié sous la rubrique Bande passante de Nyquist. Remarque : les différents auteurs utilisent des lettres différentes pour désigner le débit de données, la largeur de bande, etc.

2. Comme pour Nyquist l’équation se trouvant dans n’importe quelle édition de Data and Computer Communications de William Stallings, celle-ci est répertoriée sous Shannon Capacity Formula. Note : Différents auteurs utilisent différentes lettres pour désigner le débit de données, la largeur de bande, etc.

3. Certains sujets de la théorie de la transmission télégraphique (qui impliquaient la limite) ont été présentés à la convention d’hiver de l’AIEE, New York, N.Y., 13-17 février 1928. Ils ont été republiés en tant que « Classic Paper » dans les Proceedings of the IEEE en février 2002.

4. « Communications in the Presence of Noise » a été publié dans les Proceedings of the IRE en janvier 1949, neuf ans après avoir été écrit.

Dans le cadre de l’étude de l’IRE, les auteurs de l’article ont été invités à participer à une conférence de presse.