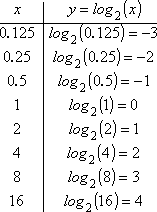Représentation graphique des fonctions logarithmiques : Introduction

Retourner à l’index des leçons | Faire les leçons dans l’ordre | Page facile à imprimer

Graphie des fonctions logarithmiques : Intro (page 1 de 3)

De par la nature du logarithme, la plupart des graphiques logarithmiques ont tendance à avoir la même forme, ressemblant à un graphique de racine carrée :

.

y = sqrt(x)	y = log2(x)

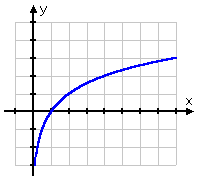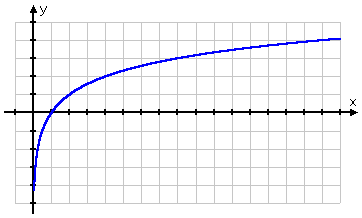
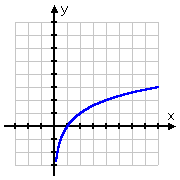
Le graphique de la racine carrée commence au point (0, 0) et s’éloigne ensuite vers la droite. En revanche, le graphique du logarithme passe par (1, 0), s’éloigne vers la droite mais glisse également sur le côté positif de l’axe des y. En se rappelant que les logarithmes sont les inverses des exponentielles, cette forme pour le graphique du logarithme est parfaitement logique : le graphique du logarithme, étant l’inverse de l’exponentielle, serait juste le « retournement » du graphique de l’exponentielle :

y = 2x	y = log2(x)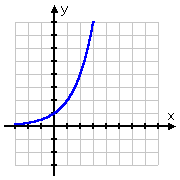
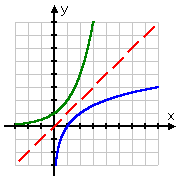
		comparaison des deux graphiques, montrant la ligne d’inversion en rouge

Il est assez simple de représenter graphiquement des exponentielles. Par exemple, pour tracer le graphique y = 2x, il suffit d’entrer certaines valeurs de x, de calculer les valeurs de y correspondantes et de tracer les points. Mais comment représenter graphiquement des logarithmes ? Il existe deux possibilités. Voici la première : Copyright © Elizabeth Stapel 2002-2011 Tous droits réservés

• Graphier y = log2(x).

Pour graphier cela « à la main », je dois d’abord me rappeler que les logs ne sont pas définis pour les x négatifs ou pour x = 0. En raison de cette restriction sur le domaine (les valeurs d’entrée) du logarithme, je ne prendrai même pas la peine d’essayer de trouver des valeurs de y pour, disons, x = -3 ou x = 0. Au lieu de cela, je vais commencer avec x = 1, et travailler à partir de là, en utilisant la définition du logarithme.

Puisque 20 = 1, alors log2(1) = 0, et (1, 0) est sur le graphique.
Puisque 21 = 2, alors log2(2) = 1, et (2, 1) est sur le graphe.
Comme 3 n’est pas une puissance de 2, alors log2(3) sera une valeur désordonnée. Je ne m’embêterai donc pas à tracer le graphique de x = 3.
Puisque 22 = 4, alors log2(4) = 2, et (4, 2) est sur le graphique.
Comme 5, 6 et 7 ne sont pas non plus des puissances de 2, je vais les sauter et passer à x = 8.
Puisque 23 = 8, alors log2(8) = 3, donc (8, 3) est sur le graphique.
La prochaine puissance de 2 est 16 : puisque 24 = 16, alors log2(16) = 4, et (16, 4) est sur le graphique.
La puissance de 2 suivante, x = 32, est trop grande à mon goût ; je n’ai pas envie de dessiner mon graphe aussi large, donc j’arrête à x = 16.

Ce qui précède me donne le point (1, 0) et quelques points à droite, mais que dois-je faire pour les valeurs de x entre 0 et 1 ? Pour cet intervalle, je dois penser en termes de puissances négatives et de réciproques. De même que la « moitié » gauche de la fonction exponentielle avait peu de points graphiques (les autres étant trop proches de l’axe des x), de même la « moitié » inférieure de la fonction logarithmique a peu de points graphiques, les autres étant trop proches de l’axe des y. Mais je peux en trouver quelques-uns :

Si 2-1 = 1/2 = 0,5, alors log2(0,5) = -1, et (0,5, -1) est sur le graphique.

Si 2-2 = 1/4 = 0,25, alors log2(0,25) = -2, et (0,25, -2) est sur le graphique.

Si 2-3 = 1/8 = 0,125, alors log2(0.125) = -3, et (0,125, -3) est sur le graphique.

La prochaine puissance de 2 (lorsque x se déplace dans cette direction) est 1/16 = 2-4, mais la valeur x pour le point (0,0625, -4) semble trop petite pour s’en préoccuper, donc je vais arrêter avec les points que j’ai déjà trouvés.

La liste de ces points me donne mon graphique en T :
Dessinant mes points puis esquissant la ligne (en pensant à ne pas aller à gauche de l’axe des ordonnées !), j’obtiens ce graphique :

Haut de page | 1 | 2 | 3 | Retour à l’index Suivant >>

.