Valeur maximale d'un nombre entier : Java Vs C vs Python | Baeldung on Computer Science

Introduction

En science des données, lorsque nous parlons d’entiers, nous faisons référence à un type de données qui représente une certaine plage d’entiers mathématiques. Nous savons que les entiers mathématiques n’ont pas de limite supérieure, mais cela pourrait poser un problème en termes de taille de mémoire, obligeant presque toutes les architectures informatiques à limiter ce type de données.

C’est donc la question que nous essayons de poser aujourd’hui : « Quelle est la valeur entière maximale que nous pouvons représenter sur une certaine machine ? »

Explication du problème

Bien, il n’y a pas une réponse unique à cette question car de nombreux facteurs influencent la réponse. Les principaux sont :

Bits de plateforme
Langage utilisé
Versions signées ou non signées

En informatique, la représentation la plus courante des nombres entiers est par un groupe de chiffres binaires (bits), stockés dans un système numérique binaire. L’ordre des octets de mémoire varie – avec bits, on peut coder entiers.

Nous pouvons voir les différences dans cet exemple simple : avec bits, nous pouvons coder des entiers de ou de $- 2^{n-1}$ $2^{n-1} - 1$ .

En général, la taille des entiers est définie par l’architecture de la machine, mais certains langages informatiques définissent également les tailles des entiers de manière indépendante. Les différents processeurs prennent en charge différents types de données, en fonction de leur propre plate-forme. Généralement, tous prennent en charge les types signés et non signés, mais seulement d’un ensemble limité et fixe de largeurs, généralement 8, 16, 32 et 64 bits.

Certains langages définissent deux ou plusieurs types de données entières, un plus petit pour préserver la mémoire et prendre moins de stockage, et un plus grand pour améliorer la plage prise en charge.

Une autre chose à garder à l’esprit est la taille des mots (également appelée longueur des mots) de la plateforme.

En informatique, un mot est l’unité de données utilisée par une conception de processeur particulière, un morceau de données de taille fixe traité comme une unité par le matériel du processeur. Lorsque nous parlons de la taille du mot, nous nous référons au nombre de bits dans un mot et c’est une caractéristique cruciale de toute architecture informatique et conception de processeur spécifique.

Les architectures actuelles ont généralement une taille de mot de 64 bits, mais il en existe aussi avec 32 bits.

L’heure des réponses

Dans cette section, nous répondrons à nos questions en partant du vieil ami C jusqu’au relativement nouveau Python, en passant par le toujours vert Java. Commençons.

3.1. C

Le langage C a été conçu en 1972, dans le but de fonctionner de la même manière sur différents types de machines. Ainsi, il ne détermine pas directement une plage pour le type de données entier car cela dépend de l’architecture de la machine.

Cependant, le C dispose de deux sortes d’entiers ; courts et longs.

Un entier court est, au minimum, de 16 bits. Ainsi, sur une machine 16 bits, il coïncide avec le format des entiers longs. Le format des entiers courts va de -32 767 à 32 767 pour la version signée et de 0 à 65 535 pour la version non signée. C’est bizarre, mais il semble que pour la version signée, il nous manque un chiffre. Cela s’explique facilement : parce que nous avons besoin d’un bit pour le signe !

Si nous fonctionnons sur un système 64 bits, nous pouvons facilement calculer que le format long peut atteindre une valeur $2^{64-1}$ , ce qui correspond à 18,446 744 073 709 551 615 pour le type de données non signé et varie de -9 223 372 036 854 775 807 à 9 223 372 036 854 775 807 dans la version signée.

Pour être complet, nous allons faire un petit tour sur le type de données entier long long. Le format long long n’est pas disponible sur C, mais uniquement sur la version C99. Il a une capacité de mémoire double de celle d’un type de données long, mais il n’est évidemment pas supporté par les compilateurs qui exigent la norme C précédente. Avec le type de données long long, on peut atteindre un énorme $2^{64-1}$ si on l’exécute sur une machine 32 bits ou plus.

3.2. Java

Pour parler de Java, il faut se rappeler qu’il fonctionne à travers une machine virtuelle. Cela nous évite toute la variabilité expliquée pour le langage C.

Java ne supporte que les versions signées des entiers. Ce sont :

octet (8 bits)
court (16 bits)
int (32 bits)
long (64 bits)

Donc, avec le format des entiers longs, on peut atteindre $2^{64-1}$ comme avec le C sur une machine 64 bits mais, cette fois, sur toutes les architectures de machines.

Cependant, avec quelques manipulations de bits, on peut obtenir des versions non signées, grâce au format char. C’est un format 16 bits, donc le format entier non signé peut atteindre 65 535.

Mais avec Java, on peut aller plus loin avec un petit hack pour pouvoir représenter de très grands nombres entiers grâce à la bibliothèque de classe BigInteger. Cette bibliothèque combine des tableaux de variables plus petites pour construire des nombres énormes. La seule limite est la mémoire physique, nous pouvons donc représenter une gamme énorme, mais encore limitée, d’entiers.

Par exemple, avec 1 kilooctet de mémoire, nous pouvons atteindre des entiers de 2 466 chiffres de long !

3.3. Python

Python prend directement en charge les entiers de précision arbitraire, également appelés entiers de précision infinie ou bignums, en tant que construction de haut niveau.

Cela signifie que, comme avec Java BigInteger, nous utilisons autant de mémoire que nécessaire pour un entier arbitrairement grand. Donc, en termes de langage de programmation, cette question ne s’applique pas du tout à Python, car le type entier simple est, théoriquement non borné.

Ce qui n’est pas non borné, c’est la taille de mot de l’interpréteur actuel, qui est la même que celle de la machine dans la plupart des cas. Cette information est disponible dans Python sous le nom de sys.maxsize, et c’est la taille de la plus grande liste ou séquence en mémoire possible, qui correspond à la valeur maximale représentable par un mot signé.

Sur une machine 64 bits, cela correspond à $2^{64-1}$ = 9 223 372 036 854 775 807.

Organigramme

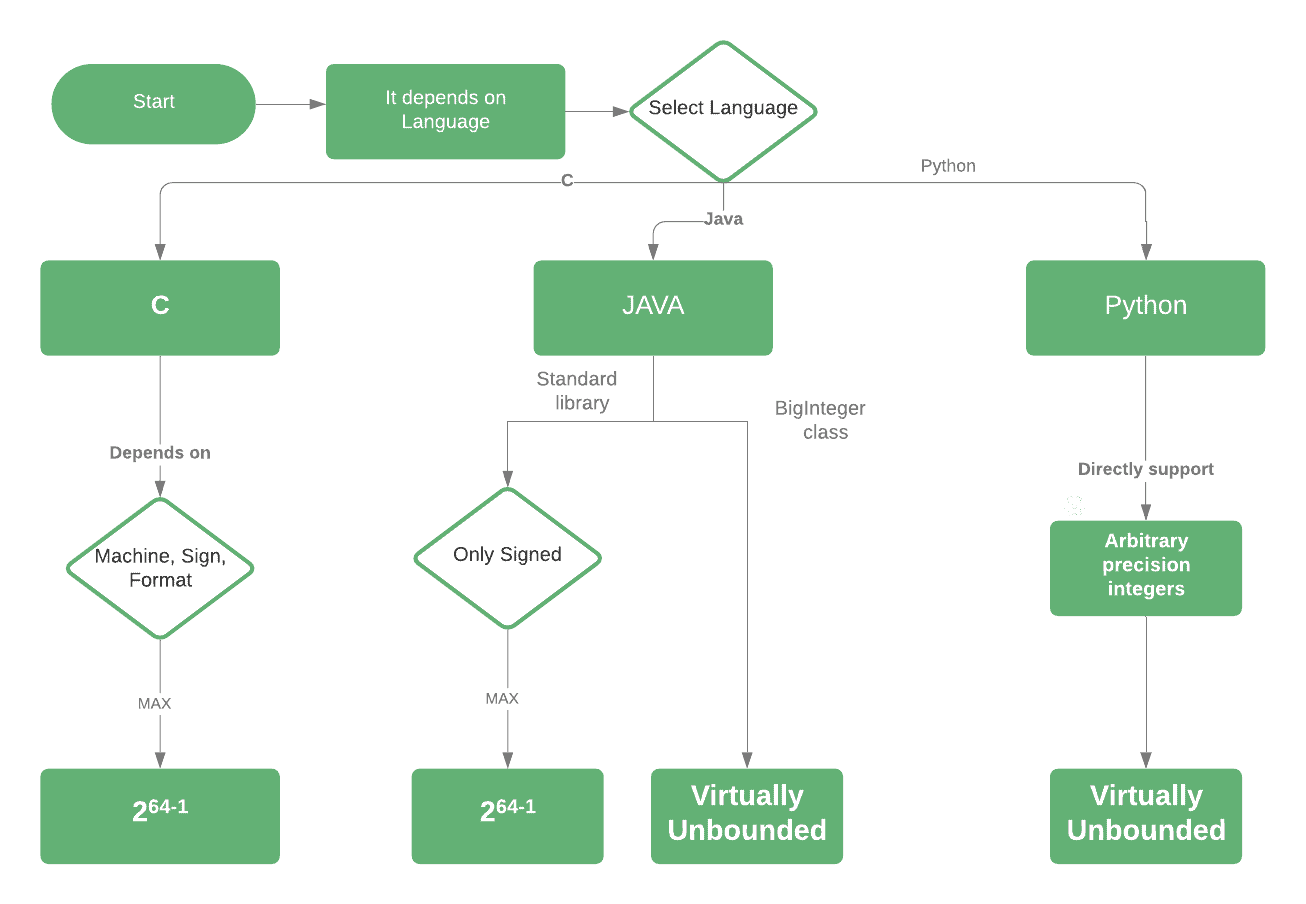
Regardons un organigramme pour résumer ce que nous avons vu jusqu’à présent:

Code réel pour chaque langage

Voici un code réel pour vérifier directement ce dont nous avons parlé jusqu’à présent. Le code démontrera les valeurs maximales et minimales des entiers dans chaque langage.

Comme ces valeurs n’existent pas sur Python, le code montre comment afficher la taille des mots de l’interpréteur actuel.

5.1. Code C

#include<bits/stdc++.h>int main() { printf("%d\n", INT_MAX); printf("%d", INT_MIN); return 0; }

5.2. Code Java

public class Test { public static void main(String args) { System.out.println(Integer.MIN_VALUE); System.out.println(Integer.MAX_VALUE); }}

5.3. Code Python

import platformplatform.architecture()import syssys.maxsize

Conclusion

Dans cet article, nous avons couvert les différences entre ces trois langages de pointe au sujet du nombre entier maximal possible. Nous avons également montré comment cette question ne s’applique pas dans certaines situations.

Cependant, il faut toujours utiliser le meilleur ajustement dans sa situation afin d’éviter la consommation de mémoire et le décalage du système.

Valeur maximale d’un nombre entier : Java Vs C vs Python