Calcolo del volume
Questa pagina spiega come calcolare il volume degli oggetti solidi, cioè quanto si potrebbe mettere in un oggetto se, per esempio, lo si riempisse di un liquido.
L’area è la misura di quanto spazio c’è all’interno di un oggetto bidimensionale (vedi la nostra pagina: Calcolo dell’area per saperne di più).
Il volume è la misura di quanto spazio c’è all’interno di un oggetto tridimensionale. La nostra pagina sulle forme tridimensionali spiega le basi di tali forme.
Nel mondo reale, il calcolo del volume non è probabilmente qualcosa che userete così spesso come il calcolo dell’area.
Tuttavia può essere ancora importante. Essere in grado di calcolare il volume ti permetterà, per esempio, di capire quanto spazio di imballaggio hai a disposizione quando traslochi, quanto spazio hai bisogno in ufficio, o quanta marmellata puoi mettere in un barattolo.
Può anche essere utile per capire cosa intendono i media quando parlano della capacità di una diga o della portata di un fiume.
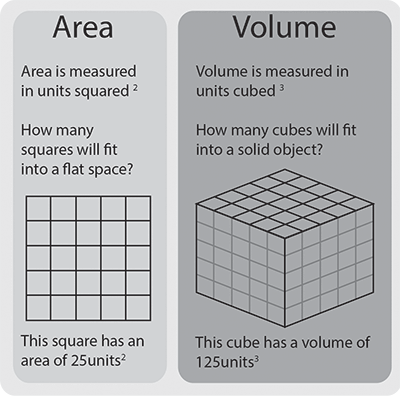
Una nota sulle unità
L’area si esprime in unità quadrate, perché sono due misure moltiplicate insieme.
Il volume si esprime in unità cubiche, perché è la somma di tre misure (lunghezza, larghezza e profondità) moltiplicate insieme. Le unità cubiche includono cm3, m3 e piedi cubici.
ATTENZIONE!
Il volume può anche essere espresso come capacità liquida.
Sistema metrico
Nel sistema metrico la capacità liquida si misura in litri, che è direttamente comparabile con la misura cubica, poiché 1ml = 1cm3. 1 litro = 1.000 ml = 1.000cm3.
Sistema imperiale/inglese
Nel sistema imperiale/inglese le misure equivalenti sono once fluide, pinte, quarti e galloni, che non sono facilmente traducibili in piedi cubici. È quindi meglio attenersi alle unità di volume dei liquidi o dei solidi.
Per saperne di più, vedi la nostra pagina sui sistemi di misura
Formule di base per il calcolo del volume
Volume dei solidi a base rettangolare

Se la formula di base per l’area di una forma rettangolare è lunghezza × larghezza, la formula di base per il volume è lunghezza × larghezza × altezza.
Come ci si riferisce alle diverse dimensioni non cambia il calcolo: si può, per esempio, usare “profondità” invece di “altezza”. L’importante è che le tre dimensioni siano moltiplicate insieme. Puoi moltiplicare nell’ordine che preferisci perché non cambierà la risposta (vedi la nostra pagina sulla moltiplicazione per saperne di più).
Una scatola delle dimensioni di 15 cm di larghezza, 25 cm di lunghezza e 5 cm di altezza ha un volume di:
15 × 25 × 5 = 1875cm3
Volume dei prismi e dei cilindri
Questa formula di base può essere estesa anche al volume di cilindri e prismi. Invece di un’estremità rettangolare, si ha semplicemente un’altra forma: un cerchio per i cilindri, un triangolo, un esagono o qualsiasi altro poligono per un prisma.
Effettivamente, per cilindri e prismi, il volume è l’area di un lato moltiplicato per la profondità o l’altezza della forma.
La formula base per il volume di prismi e cilindri è quindi:
Area della forma finale × altezza/profondità del prisma/cilindro.
Volume di coni e piramidi
Lo stesso principio di cui sopra (larghezza × lunghezza × altezza) vale per calcolare il volume di un cono o di una piramide, tranne che, poiché arrivano a un punto, il volume è solo una proporzione del totale che sarebbe se continuassero nella stessa forma fino in fondo.
Il volume di un cono o di una piramide è esattamente un terzo di quello che sarebbe per una scatola o un cilindro con la stessa base.
La formula è quindi:
Area della base o della forma finale × l’altezza del cono/piramide × 1/3
Riferisciti alla nostra pagina Calcolo dell’area se non ricordi come calcolare l’area di un cerchio o di un triangolo.
Per esempio, per calcolare il volume di un cono con un raggio di 5cm e un’altezza di 10cm:
L’area di un cerchio = πr2 (dove π (pi greco) è circa 3,14 e r è il raggio del cerchio).
In questo esempio, area della base (cerchio) = πr2 = 3,14 × 5 × 5 = 78,5cm2.
78,5 × 10 = 785
785 × 1/3 = 261,6667cm3

Volume di una sfera
Come per un cerchio, hai bisogno di π (pi) per calcolare il volume di una sfera.
La formula è 4/3 × π × raggio3.
Ti chiederai come puoi calcolare il raggio di una palla. A parte infilare un ago da maglia (efficace, ma terminale per la palla!), c’è un modo più semplice.
Puoi misurare direttamente la distanza intorno al punto più largo della sfera, per esempio, con un metro. Questo cerchio è la circonferenza e ha lo stesso raggio della sfera stessa.
La circonferenza di un cerchio si calcola come 2 x π x raggio.
Per calcolare il raggio dalla circonferenza si:
Dividere la circonferenza per (2 x π).
Esempi di lavoro: Calcolo del volume
Esempio 1

Calcolare il volume di un cilindro lungo 20cm, la cui estremità circolare ha un raggio di 2,5cm.
Prima si calcola l’area di una delle estremità circolari del cilindro.
L’area di un cerchio è πr2 (π × raggio × raggio). π (pi greco) è circa 3,14.
L’area di un’estremità è quindi:
3,14 x 2,5 x 2,5 = 19,63cm2
Il volume è l’area di un’estremità moltiplicata per la lunghezza, ed è quindi:
19.63cm2 x 20cm = 392,70cm3

Esempio 2
Cosa è più grande in volume, una sfera con raggio 2cm o una piramide con base quadrata di 2,5cm e altezza di 10cm?
Prima di tutto, calcola il volume della sfera.
Il volume di una sfera è 4/3 × π × raggio3.
Il volume della sfera è quindi:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51cm3
Poi calcola il volume della piramide.
Il volume di una piramide è 1/3 × area della base × altezza.
Area della base = lunghezza × larghezza = 2,5cm × 2,5cm = 6,25cm2
Il volume è quindi 1/3 x 6,25 × 10 = 20,83cm3
La sfera è quindi più grande in volume della piramide.
Calcolare il volume dei solidi irregolari
Così come puoi calcolare l’area delle forme bidimensionali irregolari scomponendole in forme regolari, puoi fare lo stesso per calcolare il volume dei solidi irregolari. Basta dividere il solido in parti più piccole fino a raggiungere solo solidi con cui si può lavorare facilmente.
Esempio di lavoro
Calcolare il volume di un cilindro d’acqua con altezza totale 1m, diametro di 40cm, e la cui sezione superiore è semisferica.

Prima si divide la forma in due sezioni, un cilindro e una semisfera (mezza sfera).
Il volume di una sfera è 4/3 × π × raggio3. In questo esempio il raggio è 20cm (metà del diametro). Poiché la parte superiore è semisferica, il suo volume sarà la metà di quello di una sfera piena. Il volume di questa sezione della forma quindi:
0,5 × 4/3 × π × 203 = 16.755,16cm3
Il volume di un cilindro è area della base × altezza. Qui, l’altezza del cilindro è l’altezza totale meno il raggio della sfera, che è 1m – 20cm = 80cm. L’area della base è πr2.
Il volume della sezione cilindrica di questa forma è quindi:
80 × π × 20 × 20 = 100.530,96cm3
Il volume totale di questo contenitore di acqua è quindi:
100.530,96 + 16.755,16 = 117.286,12cm3.
Questo è un numero abbastanza grande, quindi si può preferire convertirlo in 117,19 litri dividendo per 1.000 (poiché ci sono 1000cm3 in un litro). Tuttavia, è abbastanza corretto esprimerlo in cm3 poiché il problema non chiede che la risposta sia espressa in una forma particolare.
In conclusione…
Utilizzando questi principi, se necessario, dovresti ora essere in grado di calcolare il volume di quasi ogni cosa nella tua vita, che sia una cassa da imballaggio, una stanza o un cilindro d’acqua.