Come capire la base (algebra lineare)
Quando si insegna l’algebra lineare, il concetto di base è spesso trascurato. I miei studenti tutor potevano capire l’indipendenza lineare e lo span, ma vedevano la base come si potrebbe vedere un UFO: confusa ed estranea. E questo non va bene, perché la base funge da punto di partenza per gran parte dell’algebra lineare.
Abbiamo sempre bisogno di un punto di partenza, una base su cui costruire tutto il resto. Le parole non possono essere scritte senza la base di un alfabeto. Le civiltà antiche credevano che l’universo fosse formato da 4 elementi classici – acqua, terra, fuoco e aria (molto tempo fa…). E gli spazi vettoriali, la sede naturale dell’algebra lineare, hanno la base come fondamento.
Spiegherò concettualmente la base usando un’analogia con la pittura. Questa analogia è stata usata in due articoli precedenti per spiegare altri due concetti dell’algebra lineare chiamati indipendenza/dipendenza lineare e span. Raccomando di leggere prima quegli articoli, perché entrambi i concetti verranno fuori in seguito.
La base dei colori della pittura
Invece di fare matematica, supponiamo che tu sia un pittore, pronto a dipingere un capolavoro sulla tua tela. Per prima cosa, hai bisogno di comprare della vernice. Quanti colori dovresti comprare?
Ovviamente, è una cattiva idea fare un quadro guidando fino a Home Depot e comprando un barattolo di vernice ciascuno per tutte le migliaia di colori che hanno. Non avete bisogno di trenta diverse tonalità di blu, da Azure Blue, a Mountain Blue, fino a Victory Blue (idea: creare una vernice chiamata “Defeat Blue”). Hai solo bisogno di comprare vernice blu e pochi altri colori.
Se sei un pittore avaro, potresti anche dire che hai solo bisogno di comprare 5 colori per fare un dipinto: rosso, giallo, blu, bianco e nero. Certo, il verde sarebbe bello, e il rosa sarebbe figo, ma non è necessario comprare vernice rosa e verde. Dopo tutto, puoi combinare la vernice rossa e bianca per fare il rosa, o la vernice gialla e blu per fare il verde.
Rosso, giallo, blu, bianco e nero sono l’insieme minimo di colori di cui hai bisogno per fare qualsiasi altro colore. Potremmo dire che questi 5 colori formano una base per l’intero spettro dei colori.
Siccome si può fare qualsiasi altro colore usando miscele di questi cinque colori, potremmo dire che questi cinque colori coprono l’insieme di tutti i colori. Inoltre, ogni colore dell’insieme è necessario: avete bisogno di vernice bianca perché nessuna quantità di vernice gialla, rossa, nera o blu mescolata insieme creerà mai vernice bianca. In altre parole, rosso, giallo, blu, bianco e nero sono indipendenti l’uno dall’altro. Perché la tua tavolozza sia una base per tutti i colori, due condizioni devono essere vere:
- La tavolozza abbraccia l’insieme di tutti i colori.
- Tutti i colori della tavolozza sono indipendenti l’uno dall’altro.
Abbiamo appena visto che rosso, giallo, blu, bianco e nero soddisfano entrambe le condizioni. Per contrasto, ecco degli esempi di palette che non sono basi:
- Rosso, blu, bianco. Questo viola la condizione 1. Questo insieme non comprende tutti i colori. Molti colori come il giallo o il verde sono impossibili da realizzare con i colori di questo set.
- Rosso, arancione, giallo, verde, blu, viola, bianco, nero. Questo viola la condizione 2. Questi colori certamente abbracciano tutti i colori, ma non sono indipendenti. Il viola è una combinazione di rosso e blu, il verde una combinazione di giallo e blu, e così via.
La base di uno spazio vettoriale
Gli spazi vettoriali sono più astratti dei quadri, ma usano la base in modo simile. Uno spazio vettoriale è un insieme di vettori dove è possibile aggiungere vettori insieme e scalarli. Per esempio, il piano 2-D (noto anche come R²) è uno spazio vettoriale. È l’insieme di tutti i vettori “bidimensionali”, che possono essere pensati come vettori con una coordinata x e una coordinata y.
Proprio come abbiamo creato una base per l’insieme di tutti i colori, possiamo creare un insieme di vettori che formano una base di R². I requisiti della base sono quasi gli stessi della nostra base per i colori.
Base: Un insieme di n vettori, {v₁, v₂,…vₙ}, è una base di qualche spazio S se queste due condizioni sono vere:
- {v₁, v₂, …vₙ} sono linearmente indipendenti.
- {v₁, v₂,…vₙ} abbracciano l’insieme S. In altre parole, Span{v₁,v₂,…vₙ}=S
Per esempio, prendiamo i vettori (0,1) e (1,0), graficizzati qui sotto in verde. Questi vettori sono linearmente indipendenti, poiché non c’è modo di scalare (0,1) in (1,0). Inoltre, questi due vettori coprono l’intero piano 2-D, perché si può riscrivere qualsiasi punto nello spazio 2-D come una combinazione lineare di (0,1) e (1,0):
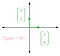
(0,1) e (1,0) formano quindi una base di R² (Questa base specifica di (0,1) e (1,0) è chiamata base standard). Tuttavia, questa non è l’unica base di R² possibile. Date un’occhiata ai vettori (1,1) e (-1,1), rappresentati graficamente qui sotto. I vettori rosa rappresentano alcune diverse combinazioni lineari:
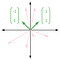
Questi due vettori sono anche linearmente indipendenti, poiché non è possibile scalare un vettore nell’altro. Dalle combinazioni lineari rosa, è anche chiaro che (1,1) e (-1,1) coprono tutto R². Pertanto, (1,1) e (-1,1) formano un’altra base per R².
Questo è un punto in cui gli spazi vettoriali sono molto diversi dall’analogia della pittura. Con i colori della vernice, abbiamo davvero solo le basi di giallo, blu, rosso, nero e bianco. Ma nel mondo degli spazi vettoriali, qualsiasi spazio ha un numero infinito di basi tra cui scegliere. In generale, una base è il più piccolo insieme di vettori possibile che può abbracciare uno spazio. È l’equivalente vettoriale dell’essere avari con la vernice, e comprare solo i colori minimi necessari.
La base ci aiuta anche a capire la struttura sottostante di uno spazio vettoriale. Per esempio, sappiamo che qualsiasi base di R² sarà composta esattamente da due vettori, come le due basi che abbiamo trovato prima. In generale:
- Per qualche spazio S, tutte le basi di S hanno lo stesso numero di vettori. Questo è stato dimostrato per la prima volta da Georg Hamel. Se una base di S è composta da 4 vettori, allora ogni base di S è composta da 4 vettori.
- Una base di uno spazio Rⁿ è composta da n vettori. Qualsiasi base per R³ (spazio tridimensionale) è composta da 3 vettori. Qualsiasi base per R⁵ (spazio a 5 dimensioni, non chiedere) è composta da 5 vettori.
Perché la base è importante (trasformazioni lineari)
Di per sé, la base non ha molto impatto. Tuttavia, tocchiamo brevemente il motivo per cui la base è così importante per l’algebra lineare.
Possiamo prendere uno spazio vettoriale e trasformarlo, “trasformare” qui significa allungare, capovolgere o ruotare lo spazio. Quando si lavora con l’algebra lineare, trasformare uno spazio vettoriale è comune come respirare. Supponiamo che io voglia trasformare il grafico A nel grafico B:

Ogni grafico ha la sua base (i vettori rosa e blu). È importante notare che sia il grafico A che il grafico B sono solo due modi diversi di rappresentare lo stesso spazio usando basi diverse. È come leggere lo stesso libro ma in due lingue diverse, come lo spagnolo e il francese.
Il passaggio dal grafico A al grafico B si chiama trasformazione lineare del grafico. Una trasformazione lineare agisce come un traduttore: Prende ogni punto del grafico B e lo sposta in ogni punto corrispondente del grafico A. Prende la parola francese e la sposta in spagnolo. Tuttavia, stiamo entrando nel mondo delle trasformazioni lineari, e questo può essere spiegato un’altra volta.
Conclusione
Ora abbiamo una comprensione più profonda di tre concetti dell’algebra lineare: base, indipendenza/dipendenza lineare e span. Questi concetti sono fondamentali per l’algebra lineare. L’indipendenza/dipendenza lineare ti dice quali vettori sono necessari in un insieme di vettori. Lo span ti dice tutte le possibili combinazioni di vettori che puoi creare. E infine, la base ti dice il più piccolo insieme di vettori necessario per coprire uno spazio vettoriale, e quindi la struttura di quello spazio.
Padroneggiare questi concetti ti darà le basi necessarie per una comprensione concreta dell’algebra lineare. Dopo tutto, una casa non può stare in piedi su una base traballante, e noi non possiamo capire l’algebra lineare senza una base. Grazie per aver letto!