Cosa si intende per fattore di potenza?

Un basso fattore di potenza riduce la capacità di distribuzione di un sistema elettrico aumentando il flusso di corrente. Pertanto, avere un basso fattore di potenza è inefficiente e costoso. Ma cos’è il fattore di potenza e cosa lo influenza?

Un tipico sistema di distribuzione è limitato nella quantità di corrente che può trasportare; il fattore di potenza, espresso in percentuale, è un indicatore della quantità di corrente totale che può essere usata per creare lavoro (potenza attiva). Più il fattore di potenza è vicino a 1,00 (100%), più bassa è la quantità di corrente necessaria per fare il lavoro.

Per esempio, un carico con un fattore di potenza di 0,80 significa che solo l’80% della potenza viene usata efficacemente per fare lavoro. In un mondo perfetto, tutta la potenza prelevata dal sistema di alimentazione sarebbe convertita in lavoro utile, ma non è così nel mondo reale. Per descrivere completamente il fattore di potenza, sono necessarie complesse equazioni. Per una comprensione più semplice, però, il Dipartimento dell’Energia degli Stati Uniti usa una semplice analogia con la potenza richiesta a un cavallo per tirare un carrello lungo un binario.

Idealmente, il cavallo dovrebbe essere posizionato davanti all’automotrice per fornire la forza di traino più efficiente; tuttavia, questo non è sempre possibile. L’angolo del traino rappresenta la variazione del fattore di potenza: più piccolo è l’angolo, migliore è il fattore di potenza, più grande è l’angolo, minore è il fattore di potenza (Figura 1).

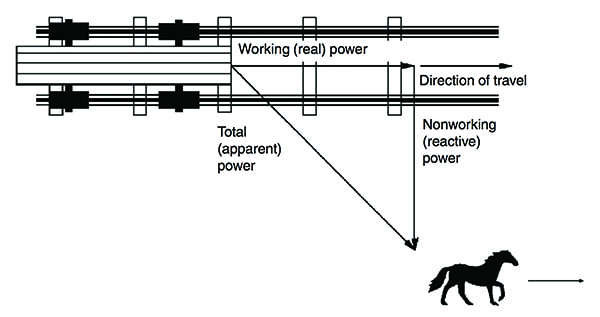
1. Gli angoli influenzano il lavoro utile. Gli angoli influenzano il lavoro utile. L’analogia mostrata qui fornisce una visualizzazione per aiutare a capire il fattore di potenza. Il fattore di potenza è definito come il rapporto tra la potenza reale (lavoro) e la potenza apparente (totale). Se il cavallo viene condotto più vicino al centro della pista, l’angolo di trazione laterale diminuisce, e la potenza reale si avvicina al valore della potenza apparente. Fonte: U.S. Department of Energy

L’energia totale richiesta per tirare l’automotrice è la potenza apparente. L’energia effettiva che muove l’automotrice è la potenza reale. L’energia non utilizzata dall’angolo di trazione del cavallo è la potenza reattiva. In altre parole, la potenza reale, indicata anche come potenza di lavoro (kW), esegue il lavoro effettivo di movimento, calore e luce. La potenza reattiva, o potenza non lavorativa (kVar), sostiene il campo magnetico di un carico reattivo (di solito induttivo). La corrente usata per creare la potenza reattiva non è usata per creare lavoro; tuttavia, questa corrente grava sul sistema di distribuzione, sul fornitore di elettricità e sulla bolletta elettrica di un impianto.

La somma vettoriale della potenza attiva e della potenza non attiva è la potenza totale (potenza apparente):

Potenza apparente = √ (potenza reale2 + potenza reattiva2)

che viene utilizzata per calcolare il fattore di potenza:

Fattore di potenza = Potenza reale / Potenza apparente = coseno dell’angolo (ϕ)

Fondamenti di tensione e corrente

Per capire il fattore di potenza, dobbiamo prima capire alcune teorie di base sulla corrente alternata (AC) e le forme d’onda ad essa associate. La tensione in un sistema AC si alterna tra positivo e negativo (in una forma sinusoidale) e costringe la corrente a comportarsi in modo simile. Questo avviene 60 volte al secondo (in un sistema a 60 Hz), da 0 a 360 gradi. A differenza dei sistemi AC, la tensione in un sistema a corrente continua (DC) costante non cambia.

Perché il valore istantaneo della tensione AC cambia continuamente, la scienza ha definito una misura diversa per le quantità AC, cioè il valore RMS (root mean square). Il valore RMS di una forma d’onda AC produce lo stesso effetto di riscaldamento di una forma d’onda DC dello stesso valore.

L’RMS è la radice quadrata della media aritmetica dei quadrati di un insieme di valori istantanei su un periodo (ciclo). Quando la tensione e la corrente sono puramente sinusoidali, la tensione e la corrente RMS possono essere trovate dalla tensione e dalla corrente di picco (pk):

VRMS = Vpk / √2

119.5 VRMS = 169 Vpk / 1.414

Similmente,

IRMS = Ipk / √2

75 ARMS = 106 Apk / 1.414

Vi starete chiedendo: cosa ha a che fare questo con il fattore di potenza? I calcoli di potenza per la corrente alternata richiedono la conoscenza della tensione RMS, della corrente RMS e della relazione di fase sinusoidale. Quindi, per riassumere, RMS è una misura dell’effetto di riscaldamento, calcolato da una forma d’onda, che permette il confronto tra AC e DC. Qualsiasi spostamento di fase da una forma d’onda sinusoidale pura indica il fattore di potenza.

Il seguente è un confronto di come il fattore di potenza influenza i kVA in uscita su due diversi carichi monofase.

Per una stufa elettrica da 9 kW (120 VAC, 75 A) con fattore di potenza (PF) in ingresso 1.0:

P = √1ϕ x 120 VAC x 75 A x 1.0 PF = 9 kW

kVA = √1ϕ x 120 VAC x 75 A = 9 kVA

Per un caricabatterie da 9 kW (120 VAC, 75 A) con 0.866 PF in ingresso:

P = √1ϕ x 120 VAC x 86.6 A x 0.866 PF = 9 kW

kVA = √1ϕ x 120 VAC x 86.6 A = 10.392 kVA

Anche se ogni carico consuma 9 kW di potenza, il fattore di potenza in ingresso del caricabatterie è 0.866. Il fattore di potenza inferiore richiede un ulteriore 11.6 A per funzionare, che è eventualmente fornito dalla società elettrica. Non solo la corrente reattiva aggiuntiva deve essere acquistata, ma anche la dimensione del sistema di distribuzione deve essere aumentata per gestire la corrente aggiuntiva.

Cosa influenza il fattore di potenza?

Il fattore di potenza si riferisce al rapporto tra la potenza attiva (potenza utile) e la potenza apparente (totale). Questo rapporto è una misura di quanto efficacemente viene usata l’elettricità.

Carichi resistivi lineari. In un sistema AC, i carichi sono classificati in base al modo in cui assorbono la corrente. Un carico resistivo lineare è un carico puramente resistivo senza componenti induttivi o capacitivi, come i riscaldatori elettrici e l’illuminazione a incandescenza. Le curve di tensione e corrente intersecano la coordinata zero nello stesso punto.

La curva di potenza (P) nella figura 2 è calcolata dalla tensione (V) e dalla corrente (I), mostrata come area positiva del grafico. In questo esempio, la tensione e la corrente sono rispettivamente 120 VRMS e 75 ARMS. Il prodotto dei due è 9 kVA o 9 kW. La tensione e la corrente sono “in fase”, e il 100% della potenza (potenza di lavoro) viene utilizzata efficacemente per fare lavoro utile. Il fattore di potenza per questo tipo di carico è 1,0.

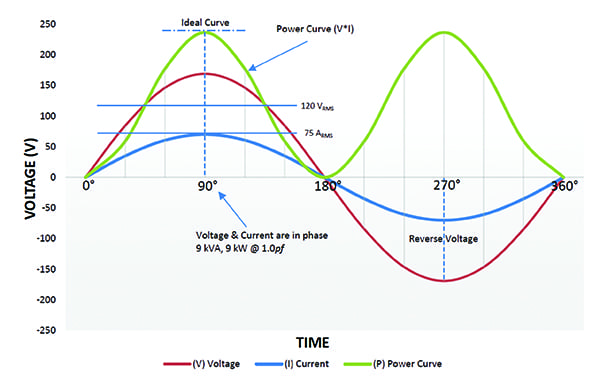
2. Carichi resistivi lineari. Tensione e corrente sono in fase con fattore di potenza uguale a 1,0 per carichi puramente resistivi. Per gentile concessione: Ametek Solidstate Controls

Carichi lineari non resistivi/reattivi. È insolito trovare carichi puramente resistivi; la maggior parte dei carichi ha una componente reattiva aggiuntiva. Questi carichi non resistivi/reattivi costituiscono una grande percentuale di tutti i carichi. La forma d’onda della corrente è spostata dalla forma d’onda della tensione in modo che sia “fuori fase”. Se il carico è induttivo, la corrente è in ritardo rispetto alla tensione; se il carico è capacitivo, la corrente è in vantaggio.

Le strutture industriali tendono ad avere carichi con fattore di potenza in ritardo (carichi induttivi). Questi tipi di carichi possono essere motori a induzione, bobine e trasformatori. I carichi con fattore di potenza principale (carichi capacitivi) sono meno comuni e sono di solito cavi sotterranei o certi alimentatori a commutazione.

Nella Figura 3, lo stesso carico della Figura 2 ha ora la forma d’onda di tensione e corrente fuori fase di 30 gradi. Poiché si tratta di una forma d’onda induttiva, la corrente è ora in ritardo.

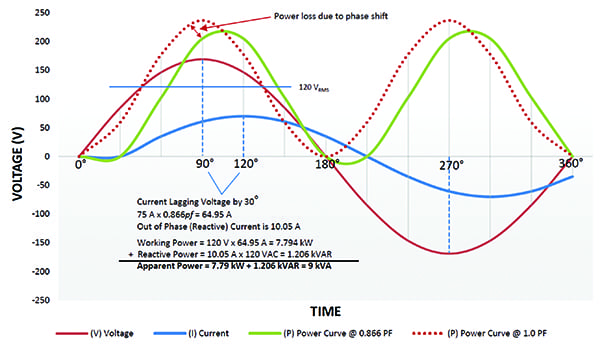
3. Carichi induttivi. La tensione e la corrente sono fuori fase per i carichi lineari non resistivi/reattivi. In questo esempio di carico induttivo, la corrente ritarda la tensione di 30 gradi con un fattore di potenza di 0,866. Per gentile concessione: Ametek Solidstate Controls

Carichi non lineari-armonici. Gli ambienti industriali di oggi non hanno solo carichi resistivi, induttivi e capacitivi, ma molti includono anche attrezzature basate sullo stato solido, come alimentatori a commutazione, azionamenti CC, azionamenti a frequenza variabile (VFD), reattori elettronici, saldatori ad arco e forni a temperatura controllata. Questi sono tutti carichi non lineari, o carichi per i quali la corrente non è sinusoidale, anche quando la tensione è sinusoidale. La natura non sinusoidale di queste forme d’onda si esprime con le armoniche.

Le armoniche sono forme d’onda di ampiezza variabile a frequenze che sono multipli della frequenza fondamentale della tensione (50 Hz o 60 Hz). Sono sovrapposte alla forma d’onda sinusoidale della corrente per creare la forma d’onda totale della corrente. La figura 4 è un esempio di tale forma d’onda di corrente.

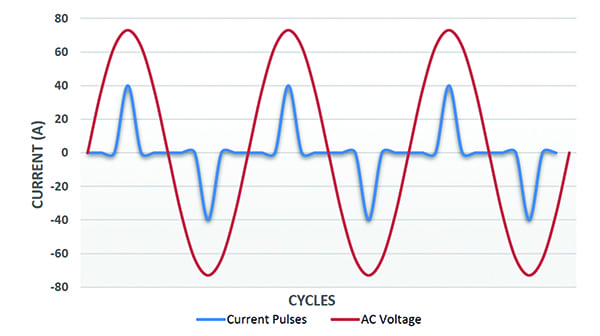
4. Carichi non lineari. Questo grafico mostra le forme d’onda di tensione e corrente di un’alimentazione non lineare con armoniche. È mostrato senza uno spostamento di fase della corrente di 30 gradi per chiarezza. Per gentile concessione: Ametek Solidstate Controls

Il valore RMS dell’intera corrente si trova sommando il valore RMS di ogni corrente armonica. Data una forma d’onda di 60 Hz, questo significa che la frequenza della seconda armonica sarebbe 120 Hz (60 Hz x 2 = 120 Hz) e le frequenze della terza, quarta e quinta armonica sarebbero rispettivamente 180 Hz, 240 Hz e 300 Hz. Come multipli della frequenza fondamentale, le armoniche possono essere espresse come 2f, 3f, 4f, ecc.

La distorsione armonica totale della corrente (THD) è la somma di tutte le componenti armoniche della forma d’onda della corrente rispetto alla componente fondamentale dell’onda corrente. Come mostrato di seguito, è un rapporto tra il valore RMS delle armoniche della corrente e il valore RMS della corrente fondamentale.

ITHD = RMS delle armoniche di corrente / RMS della corrente fondamentale = √(I22 + I32 + I42 + …) / I1 x 100%

Per forme d’onda puramente sinusoidali, lo spostamento di fase tra tensione e corrente è sufficiente per quantificare il fattore di potenza (PF). Per le forme d’onda che non sono sinusoidali, il termine fattore di potenza di spostamento (DpPF) è usato per quantificare lo spostamento di fase tra i fondamentali delle due forme d’onda (le componenti 50-Hz o 60-Hz). Per le stesse forme d’onda non sinusoidali, si definisce un termine per quantificare l’effetto delle armoniche sul PF. Questo termine è chiamato fattore di potenza di distorsione (DF).

DF = 1 / √(1 + THD2)

Per trovare il fattore di potenza totale (PFT), si usa la seguente equazione:

PFT = DF x DpPF

Correlazioni del fattore di potenza

Per i carichi lineari, il triangolo di potenza è un triangolo rettangolo che mostra le relazioni tra potenza attiva, reattiva e apparente. La relazione tra la potenza di lavoro e quella apparente è il PF. Il valore può variare da 0,0 a 1,0.

La potenza di lavoro, chiamata anche potenza vera, potenza reale o potenza attiva, esegue il lavoro effettivo di movimento/riscaldamento/illuminazione ecc. e si misura in watt (W). La potenza reattiva sostiene il campo magnetico o elettrico nei dispositivi, come le bobine dei solenoidi, gli avvolgimenti dei motori, gli avvolgimenti dei trasformatori, i condensatori e i reattori, senza fare lavoro effettivo. Questa energia extra si misura in volt-ampere reattivi (VAR) ed è talvolta chiamata potenza “senza watt”. La potenza apparente combina la potenza di lavoro e la potenza reattiva e si misura in volt-ampere (VA).

L’angolo di fase (ϕ) in gradi, rappresenta l'”inefficienza” del carico e corrisponde all’impedenza reattiva totale (Z) al flusso di corrente nel carico. Più grande è l’angolo di fase, maggiore è la potenza reattiva. I carichi non lineari aggiungono un elemento extra alla potenza totale (apparente) senza aggiungere alla potenza attiva, diminuendo ulteriormente il fattore di potenza. ■

-David McKinnon è ingegnere senior delle applicazioni presso Ametek Solidstate Controls. Un ringraziamento speciale a Bogdan Proca, PhD e Doug King per i loro contributi.