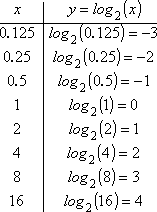Funzioni logaritmiche grafiche: Introduzione

Ritorna all’indice delle lezioni | Fai le lezioni in ordine | Pagina facile da stampare

Grafico delle funzioni logaritmiche: Introduzione (pagina 1 di 3)

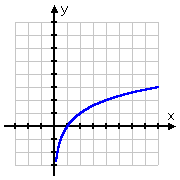
Per natura del logaritmo, la maggior parte dei grafici logici tende ad avere la stessa forma, simile ad un grafico a radice quadrata:

y = sqrt(x)	y = log2(x)

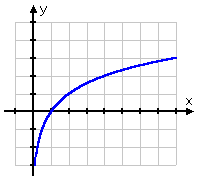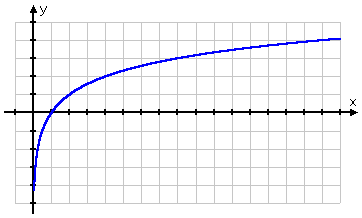
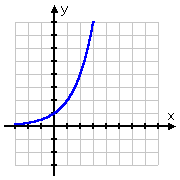
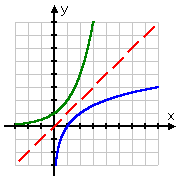
Il grafico della radice quadrata inizia nel punto (0, 0) e poi va verso destra. D’altra parte, il grafico del log passa per (1, 0), andando a destra ma anche scendendo lungo il lato positivo dell’asse y. Ricordando che i log sono gli inversi degli esponenziali, questa forma del grafico del log ha perfettamente senso: il grafico del log, essendo l’inverso dell’esponenziale, sarebbe semplicemente il “capovolgimento” del grafico dell’esponenziale:

y = 2x	y = log2(x)
confronto dei due grafici, mostrando la linea di inversione in rosso

È abbastanza semplice tracciare il grafico degli esponenziali. Per esempio, per rappresentare y = 2x, basta inserire alcuni valori di x, calcolare i corrispondenti valori di y e tracciare i punti. Ma come si fa a tracciare i log? Ci sono due opzioni. Ecco la prima: Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved

• Grafico y = log2(x).

Per fare il grafico “a mano”, devo prima ricordare che i log non sono definiti per x negativo o per x = 0. A causa di questa restrizione sul dominio (i valori di ingresso) del log, non mi preoccuperò nemmeno di cercare di trovare i valori di y per, diciamo, x = -3 o x = 0. Invece, inizierò con x = 1, e lavorerò da lì, usando la definizione del log.

Poiché 20 = 1, allora log2(1) = 0, e (1, 0) è sul grafico.
Poiché 21 = 2, allora log2(2) = 1, e (2, 1) è sul grafico.
Poiché 3 non è una potenza di 2, allora log2(3) sarà qualche valore disordinato. Quindi non mi preoccuperò di tracciare il grafico di x = 3.
Poiché 22 = 4, allora log2(4) = 2, e (4, 2) è sul grafico.
Dato che 5, 6 e 7 non sono potenze di 2, le salto e passo a x = 8.
Poiché 23 = 8, allora log2(8) = 3, quindi (8, 3) è sul grafico.
La prossima potenza di 2 è 16: poiché 24 = 16, allora log2(16) = 4, e (16, 4) è sul grafico.
La prossima potenza di 2, x = 32, è troppo grande per i miei gusti; non ho voglia di disegnare il mio grafico così largo, quindi mi fermo a x = 16.

Il precedente mi dà il punto (1, 0) e alcuni punti a destra, ma cosa faccio per i valori di x tra 0 e 1? Per questo intervallo, devo pensare in termini di potenze negative e reciproci. Come la “metà” sinistra della funzione esponenziale ha pochi punti graficabili (il resto è troppo vicino all’asse delle x), così anche la “metà” inferiore della funzione log ha pochi punti graficabili, il resto è troppo vicino all’asse delle y. Ma posso trovarne alcuni:

Siccome 2-1 = 1/2 = 0.5, allora log2(0.5) = -1, e (0.5, -1) è sul grafico.

Siccome 2-2 = 1/4 = 0.25, allora log2(0.25) = -2, e (0.25, -2) è sul grafico.

Siccome 2-3 = 1/8 = 0.125, allora log2(0.125) = -3, e (0.125, -3) è sul grafico.

La prossima potenza di 2 (come x si muove in questa direzione) è 1/16 = 2-4, ma il valore di x per il punto (0.0625, -4) sembra troppo piccolo per preoccuparsene, quindi lascerò perdere i punti che ho già trovato.

L’elenco di questi punti mi dà il mio grafico a T:
Disegnando i miei punti e poi disegnando la linea (ricordando di non andare a sinistra dell’asse y!), ottengo questo grafico:

Top | 1 | 2 | 3 | Return to Index Next >>