Guide e consigli online per la preparazione di SAT / ACT

Se stai studiando trigonometria o calcolo – o ti stai preparando – avrai bisogno di familiarizzare con il cerchio unitario. Il cerchio unitario è uno strumento essenziale usato per risolvere il seno, il coseno e la tangente di un angolo. Ma come funziona? E quali informazioni devi conoscere per usarlo?

In questo articolo, ti spieghiamo cos’è il cerchio unitario e perché dovresti conoscerlo. Ti diamo anche tre consigli per aiutarti a ricordare come usare il cerchio unitario.

Feature Image: Gustavb/Wikimedia

Il cerchio unitario: Un’introduzione di base

Il cerchio unitario è un cerchio con un raggio di 1. Questo significa che per qualsiasi linea retta disegnata dal punto centrale del cerchio a qualsiasi punto lungo il bordo del cerchio, la lunghezza di quella linea sarà sempre uguale a 1. (Questo significa anche che il diametro del cerchio sarà uguale a 2, poiché il diametro è uguale al doppio della lunghezza del raggio.)

Tipo, il punto centrale del cerchio unitario è dove l’asse x e l’asse y si intersecano, o alle coordinate (0, 0):

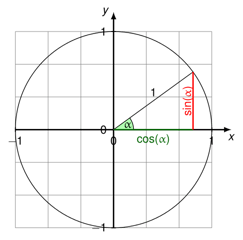
Il cerchio unitario, o cerchio trigonometrico come è anche conosciuto, è utile da conoscere perché ci permette di calcolare facilmente coseno, seno e tangente di qualsiasi angolo compreso tra 0° e 360° (o 0 e 2π radianti).

Come si può vedere nel diagramma sopra, disegnando un raggio in un angolo qualsiasi (segnato da ∝ nell’immagine), si crea un triangolo rettangolo. In questo triangolo, il coseno è la linea orizzontale e il seno è la linea verticale. In altre parole, coseno = coordinata x, e seno = coordinata y. (La linea più lunga del triangolo, o ipotenusa, è il raggio e quindi è uguale a 1.)

Perché tutto questo è importante? Ricorda che puoi risolvere le lunghezze dei lati di un triangolo usando il teorema di Pitagora, o $a^2+b^2=c^2$ (in cui a e b sono le lunghezze dei lati del triangolo, e c è la lunghezza dell’ipotenusa).

Sappiamo che il coseno di un angolo è uguale alla lunghezza della linea orizzontale, il seno è uguale alla lunghezza della linea verticale e l’ipotenusa è uguale a 1. Pertanto, possiamo dire che la formula per qualsiasi triangolo rettangolo nel cerchio unitario è la seguente:

$cos^2θ+sin^2θ=1^2$

Siccome $1^2=1$, possiamo semplificare questa equazione come segue:

$cos^2θ+sin^2θ=1$

Si noti che questi valori possono essere negativi a seconda dell’angolo formato e in quale quadrante cadono le coordinate x e y (lo spiegherò in dettaglio più avanti).

Ecco una panoramica di tutti i principali angoli in gradi e radianti sul cerchio unitario:

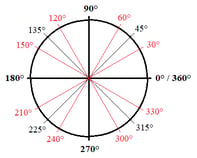
Unit Circle – Degrees

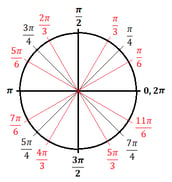
Unit Circle – Radians

Ma se non si forma un triangolo? Guardiamo cosa succede quando l’angolo è 0°, creando una linea retta orizzontale lungo l’asse x:

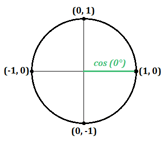
Su questa linea, la coordinata x è uguale a 1 e la coordinata y a 0. Sappiamo che il coseno è uguale alla coordinata x e il seno è uguale alla coordinata y, quindi possiamo scrivere questo:

• $\cos0°=1$
• $\sin0°=0$

E se l’angolo è di 90° e fa una linea perfettamente verticale lungo l’asse y?

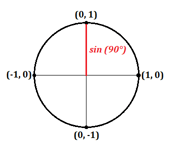
Qui possiamo vedere che la coordinata x è uguale a 0 e la coordinata y a 1. Questo ci dà i seguenti valori per seno e coseno:

• $\cos90°=0$
• $\sin90°=1$

Questo slogan vale sicuramente se non siete amanti della matematica.

Perché dovresti conoscere il cerchio unitario

Come detto sopra, il cerchio unitario è utile perché ci permette di risolvere facilmente il seno, coseno o tangente di qualsiasi grado o raggio. È particolarmente utile conoscere il grafico del cerchio unitario se hai bisogno di risolvere certi valori di trigonometria per i compiti di matematica o se ti stai preparando a studiare il calcolo.

Ma come esattamente può aiutarti conoscere il cerchio unitario? Diciamo che ti viene dato il seguente problema in un test di matematica e non ti è permesso di usare una calcolatrice per risolverlo:

$sin30°$

Da dove cominci? Diamo di nuovo un’occhiata al grafico del cerchio unitario – questa volta con tutti gli angoli maggiori (sia in gradi che in radianti) e le loro coordinate corrispondenti:

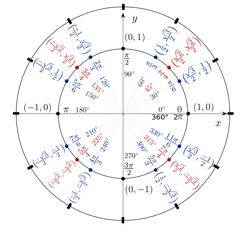Jim.belk/Wikimedia

Non farti sopraffare! Ricordate, tutto quello che state risolvendo è $\sin30°$. Guardando questo grafico, possiamo vedere che la coordinata y è uguale a $1/2$ a 30°. E siccome la coordinata y è uguale al seno, la nostra risposta è la seguente:

$\sin30°=1/2$

Ma cosa succede se hai un problema che usa i radianti invece dei gradi? Il procedimento per risolverlo è sempre lo stesso. Diciamo, per esempio, che hai un problema che assomiglia a questo:

$\cos{3π}/4}$

Ancora una volta, usando il grafico sopra, possiamo vedere che la coordinata x (o coseno) per ${3π}/4$ (che è uguale a 135°) è $-{√2}/2$. Ecco come sarebbe allora la nostra risposta a questo problema:

$\cos({3π}/4)=-{√2}/2$

Tutto questo è abbastanza facile se hai il grafico del cerchio unitario di cui sopra da usare come riferimento. Ma la maggior parte (se non tutte) delle volte, questo non sarà il caso, e ci si aspetta che tu risponda a questo tipo di domande di matematica usando solo il tuo cervello.

Come puoi quindi ricordare il cerchio delle unità? Continua a leggere per i nostri migliori consigli!

Come ricordare il cerchio delle unità: 3 consigli essenziali

In questa sezione, ti diamo i nostri migliori consigli per ricordare il cerchio di trigonometria in modo da poterlo usare con facilità per qualsiasi problema di matematica che lo richieda.

Non raccomanderei di esercitarsi sul cerchio delle unità con i post-it, ma, ehi, è un inizio.

#1: Memorizza gli angoli e le coordinate comuni

Per usare efficacemente il cerchio unitario, dovrai memorizzare gli angoli più comuni (sia in gradi che in radianti) così come le loro corrispondenti coordinate x e y.

Il diagramma qui sopra è un utile grafico del cerchio unitario da guardare, poiché include tutti i principali angoli sia in gradi che in radianti, oltre ai loro corrispondenti punti di coordinate lungo gli assi x e y.

Ecco un grafico che elenca queste stesse informazioni in forma di tabella:

Angolo (Gradi)	Angolo (Radianti)	Coordinate del punto sul cerchio
0° / 360°	0 / 2π	(1, 0)
30°	$π/6$	$({√3}/2, 1/2)$
45°	$π/4$	$({√2}/2, {√2}/2)$
60°	$π/3$	$(1/2,{√3}/2)$
	90°	$π/2$	(0, 1)
120°	${2π}/3$	$(-1/2, {√3}/2)$
135°	${3π}/4$	$(-{√2}/2, {√2}/2)$
	150°	${5π}/6$	$(-{√3}/2, 1/2)$
180°	π	(-1, 0)
210°	${7}/6$	$(-{√3}/2, -1/2)$
225°	${5π}/4$	$(-{√2}/2, -{√2}/2)$
240°	${4π}/3$	$(-1/2, -{√3}/2)$
270°	${3π}/2$	(0, -1)
300°	${5π}/3$	$(1/2, -{√3}/2)$
	315°	${7π}/4$	$({√2}/2, -{√2}/2)$
330°	${11π}/6$	$({√3}/2, -1/2)$

Ora, mentre sei più che benvenuto a cercare di memorizzare tutte queste coordinate e angoli, questo è un sacco di roba da ricordare.

Fortunatamente, c’è un trucco che puoi usare per aiutarti a ricordare le parti più importanti del cerchio unitario.

Guardate le coordinate qui sopra e noterete un chiaro schema: tutti i punti (esclusi quelli a 0°, 90°, 270° e 360°) alternano solo tre valori (sia positivi che negativi):

• $1/2$
• ${√2}/2$
• ${√3}/2$

Ogni valore corrisponde a una linea breve, media o lunga sia per il coseno che per il seno:

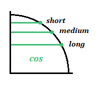
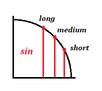
Ecco cosa significano queste lunghezze:

• Linea orizzontale o verticale corta = $1/2$
• Linea orizzontale o verticale media = $√2}/2$
• Linea orizzontale o verticale lunga = $√3}/2$

Per esempio, se stai cercando di risolvere $\cos{π/3}$, dovresti sapere subito che questo angolo (che è uguale a 60°) indica una linea orizzontale corta sul cerchio unitario. Pertanto, la sua corrispondente coordinata x deve essere uguale a $1/2$ (un valore positivo, poiché $π/3$ crea un punto nel primo quadrante del sistema di coordinate).

Infine, mentre è utile memorizzare tutti gli angoli nella tabella qui sopra, nota che gli angoli di gran lunga più importanti da ricordare sono i seguenti:

• 30° / $π/6$
• 45° / $π/4$
• 60° / $π/3$

Tratta i tuoi negativi e positivi come se fossero cavi che possono potenzialmente ucciderti se collegati in modo errato.

#2: Impara cosa è negativo e cosa è positivo

E’ fondamentale essere in grado di distinguere le coordinate x e y positive e negative in modo da trovare il valore corretto per un problema di trigonometria. Come promemoria, se una coordinata sul cerchio unitario sarà positiva o negativa dipende da quale quadrante (I, II, III o IV) il punto cade sotto:

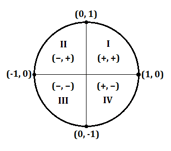
Ecco un grafico che mostra se una coordinata sarà positiva o negativa in base al quadrante in cui si trova un particolare angolo (in gradi o radianti):

Quadrante	Coordinata X (Coseno)	Y-Coordinata (Seno)
I	+	+
II	–	+
III	–	–
IV	+	–

Ad esempio, diciamo che ti viene dato il seguente problema in un test di matematica:

$\cos210°$

Prima ancora di provare a risolverlo, dovresti essere in grado di riconoscere che la risposta sarà un numero negativo poiché l’angolo 210° cade nel quadrante III (dove le coordinate x sono sempre negative).

Ora, usando il trucco che abbiamo imparato nel suggerimento 1, puoi capire che un angolo di 210° crea una lunga linea orizzontale. Quindi, la nostra risposta è la seguente:

$\cos210°=-{√3}/2$

#3: Sapere come risolvere la tangente

Infine, è essenziale sapere come usare tutte queste informazioni sul cerchio trigonometrico e sul seno e coseno per poter risolvere la tangente di un angolo.

In trigonometria, per trovare la tangente di un angolo θ (sia in gradi che in radianti), si divide semplicemente il seno per il coseno:

$$$tanθ={{sinθ}/{\cosθ}$

Per esempio, diciamo che stai cercando di rispondere a questo problema:

$$$300°$

Il primo passo è quello di impostare un’equazione in termini di seno e coseno:

$$$$300°={sin300°}/{\cos300°}$

Ora, per risolvere la tangente, abbiamo bisogno di trovare il seno e il coseno di 300°. Dovresti essere in grado di riconoscere rapidamente che l’angolo 300° cade nel quarto quadrante, il che significa che il coseno, o coordinata x, sarà positivo, e il seno, o coordinata y, sarà negativo.

Si dovrebbe anche sapere subito che l’angolo 300° crea una linea orizzontale corta e una linea verticale lunga. Pertanto, il coseno (la linea orizzontale) sarà uguale a $1/2$, e il seno (la linea verticale) sarà uguale a $-{√3}/2$ (un valore y negativo, poiché questo punto è nel quadrante IV).

Ora, per trovare la tangente, basta inserire e risolvere:

$ $\tan300°={-{√3}/2}/{1/2}$

$$\tan300°=-√3$

E’ ora di fare le fusa alle tue abilità matematiche!

Set di domande pratiche sul cerchio delle unità

Ora che sai com’è fatto il cerchio delle unità e come usarlo, mettiamo alla prova ciò che hai imparato con alcuni problemi pratici.

Domande

1. $\sin45°$
2. $cos240°$
3. $cos{5π}/3$
4. ${tan{2π}/3$

Risposte

1. ${√2}/2$
2. $-1/2$
3. $1/2$
4. $-√3$

Spiegazioni delle risposte

#1: $\sin45°$

Con questo problema, ci sono due informazioni che dovresti essere in grado di identificare subito:

• La risposta sarà positiva, poiché l’angolo di 45° è nel quadrante I, e il seno di un angolo è uguale alla coordinata y

• L’angolo di 45° crea una linea verticale di media lunghezza (per il seno)

Siccome 45° indica una linea positiva di media lunghezza, la risposta corretta è ${√2}/2$.

Se non sei sicuro di come capirlo, disegna un diagramma che ti aiuti a determinare se la lunghezza della linea sarà breve, media o lunga.

#2: $\cos240°$

Come il problema #1 qui sopra, ci sono due informazioni che dovresti essere in grado di cogliere rapidamente con questo problema:

• La risposta sarà negativa, poiché l’angolo 240° è nel quadrante III, e il coseno di un angolo è uguale alla coordinata x

• L’angolo 240° crea una linea orizzontale corta (per il coseno)

Siccome 240° indica una linea negativa e corta, la risposta corretta è $-1/2$.

#3: $cos{5π}/3$

A differenza dei problemi precedenti, questo problema usa i radianti invece dei gradi. Anche se questo potrebbe far sembrare il problema più difficile da risolvere, in realtà usa gli stessi passi di base degli altri due problemi.

In primo luogo, si dovrebbe riconoscere che l’angolo ${5π}/3$ è nel quadrante IV, quindi la coordinata x, o coseno, sarà un numero positivo. Dovresti anche essere in grado di dire che ${5π}/3$ crea una breve linea orizzontale.

Questo ti dà abbastanza informazioni per determinare che la risposta è $1/2$.

#4: ${tan{2π}/3$

Questo problema riguarda la tangente invece del seno o del coseno, il che significa che richiede un po’ più di matematica da parte nostra. Prima di tutto, ricordiamo la formula di base per trovare la tangente:

$ $ $tan θ={sin θ}/{cos θ}$

Ora, prendiamo il grado che ci è stato dato-{2π}/3$-e inseriamolo in questa equazione:

$$tan {2π}/3={{sin {2π}/3}/{\cos {2π}/3}$

Ora dovresti essere in grado di risolvere il seno e il coseno separatamente usando ciò che hai memorizzato sul cerchio unitario. Poiché l’angolo ${2π}/3$ è nel quadrante II, la coordinata x (o coseno) sarà negativa, e la coordinata y (o seno) sarà positiva.

In seguito, dovresti essere in grado di determinare in base al solo angolo che la linea orizzontale è una linea corta, e la linea verticale è una linea lunga. Questo significa che il coseno è uguale a $-1/2$ e il seno è uguale a ${√3}/2$.

Ora che abbiamo capito questi valori, tutto quello che dobbiamo fare è inserirli nella nostra equazione iniziale e risolvere la tangente:

$${2π}/3={√3}/2}/{-1/2}$

$$${2π}/3=-√3$

Cosa c’è dopo?

Se stai per sostenere il SAT o l’ACT, avrai bisogno di conoscere un po’ di trigonometria per poter fare bene la sezione di matematica. Dai un’occhiata alle nostre guide di esperti sulla trigonometria al SAT e all’ACT, così potrai imparare esattamente ciò che dovrai sapere per il giorno del test!

Oltre a memorizzare il cerchio delle unità, è una buona idea imparare come inserire i numeri e come inserire le risposte. Leggi le nostre guide per imparare tutto su queste due utili strategie, che puoi usare in qualsiasi test di matematica, compresi il SAT e l’ACT!

Hai amici che hanno bisogno di aiuto nella preparazione dei test? Condividi questo articolo!