Qual è la differenza tra PNP e NPN?

Questo articolo è apparso su Microwaves & RF ed è stato pubblicato qui con l’autorizzazione.

Cosa imparerai:

• Il throughput massimo di un canale in funzione della frequenza dei simboli e della larghezza di banda.
• Il throughput massimo di un canale in funzione dell’interferenza del rumore.
• Come le considerazioni sul throughput arrivano fino all’utente.

È una cosa molto facile e normale concentrarsi sulle caratteristiche principali dei componenti principali di un sistema o collegamento di comunicazione, e considerare altri elementi e questioni come periferici e non così importanti. Il fatto che ciò sia accaduto in modo sorprendente con i collegamenti di comunicazione satellitare, specialmente quelli mobili remoti, è il motivo di questa missiva.

Ecco una situazione ipotetica. Sei un soldato. Sei schierato in una zona montuosa del Medio Oriente, porti con te un vecchio terminale satellitare Intelsat per un accesso immediato al quartier generale, e il quartier generale ha affittato un transponder a 72-MHz per il tuo uso esclusivo.

Un posto carino e sicuro è una caverna, così si stringe un cavo di comunicazione al terminale satellitare all’ingresso della caverna e ci si siede per fare il check-in con la propria stazione di lavoro che è collegata al terminale con un modem QPSK (quadrature phase-shift keying). Il check-in va bene, ma la comunicazione è pessima. La compagnia satellitare ti garantisce 72 Mb/s (1 bit per Hz), ma ottieni a malapena meno di 35 Mb/s. Avresti dovuto prendere un terminale più nuovo? Dovresti usare un altro sistema?

Nyquist Maximum Data Rates

La vera risposta è ciò che Harry Nyquist e Claude Shannon hanno detto sulla velocità massima dei dati su ogni canale, incluso il cavo di comunicazione. Harry Nyquist ha notato, come è stato accuratamente documentato1, che il numero massimo di bit che si può ottenere attraverso un canale (rumore non considerato) è:

Max R = 2 H Log2V

dove H è la larghezza di banda del canale e V è il numero di simboli discreti (binary phase-shift keying, o BPSK, è 2, QPSK è 4, ecc).

Se non avete familiarità con il log2, non è difficile una volta che vi siete abituati. Il log2V è semplicemente l’esponente a cui 2 deve essere elevato per essere uguale a V. Così, se V è BPSK (2), allora l’espressione log2V è semplicemente 1, poiché 21 è effettivamente 2; e se V è QPSK (4), allora l’espressione log2V è 2 poiché 22 è effettivamente 4, e così via.

Se state usando un cavo Cat 3 da 10-MHz, allora la massima velocità di dati IN ENTRATA nel terminale satellitare è BPSK 20 Mb/s, QPSK 40 Mb/s, e 8PSK 30 Mb/s, in funzione delle relazioni log2. La figura 1 mostra il numero di stati e il loro log all’equivalente in base 2. Pertanto, il limite di Nyquist, usando il modem QPSK, è di 40 Mb/s.

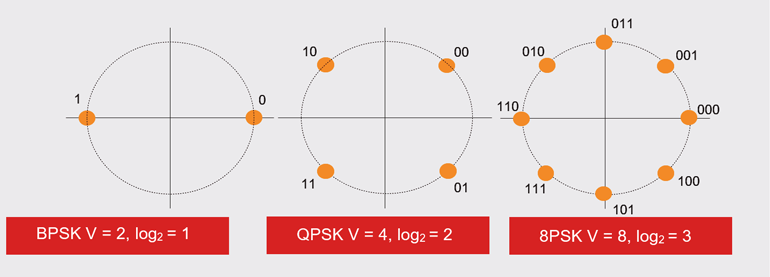1. BPSK, avendo due stati, ha un valore log2 di 1; QPSK, avendo quattro stati, ha un valore log2 di 2; e così via.

Shannon Maximum Data Rates

Bene, Harry Nyquist stava lavorando al problema della massima velocità di trasmissione dati senza considerare il rumore mentre Claude Shannon lo stava lavorando strettamente in funzione del rumore. La sua equazione2 dice:

Max R = H log2 (1 + SNR)

dove H è di nuovo la larghezza di banda del canale e il SNR è la potenza del segnale diviso la potenza del rumore, generalmente data in dB. Supponiamo che l’SNR su quello stesso cavo Cat 3 sia circa 30 dB o 1.000 in numeri grezzi (l’SNR deve essere riconvertito al suo valore razionale per calcolare un esponenziale). Dato che abbiamo fatto una progressione delle esponenziali di 2, possiamo continuare a farlo. La figura 2 mostra questa progressione.

2. Un numero, mostrato sulla linea superiore, ha un valore esponenziale, mostrato sulla linea inferiore, e dimostra l’importanza della temperatura del rumore del sistema in relazione al throughput di un canale.

Se arrotondiamo un po’ per semplicità, 1.001 è più vicino a 1.024 di qualsiasi altro incremento e 2 elevato alla decima potenza vi dà un valore molto più vicino di qualsiasi altro esponente. Seduto nella tua caverna con un cavo Cat 3 a 10 MHz di larghezza di banda, Claude Shannon dice che dovresti ottenere una velocità di trasmissione dati di 10 x 106 (10) = 100 Mb/s.

Se Claude Shannon dice che puoi ottenere una velocità massima di trasmissione dati nel terminale di comunicazione satellitare di 100 Mb/s e Harry Nyquist dice che puoi ottenere solo 40 Mb/s da e verso la tua workstation dotata di QPSK, chi ha ragione? L’Università di Notre Dame ha una squadra di calcio accademicamente limitata ma relativamente buona. D’altra parte, ha una grande banda musicale perché i musicisti eccezionali sono spesso studenti liceali eccezionali. Per entrare in campo, la banda deve marciare attraverso due archi, uno che permette 15 membri a testa e uno che ne permette 10. Come si forma la banda? Beh, allo stesso modo, Nyquist e Shannon non sono in competizione. Sono solo due porte diverse con due vincoli diversi.

Non è solo il sistema principale. Sono i go-intas e i go-outas fino alle mani che scrivono sulla tastiera. E gli articoli originali pubblicati dal fisico Nyquist3 e dal matematico/ingegnere Shannon4 hanno ancora qualcosa da dirci.

1. Un esempio dell’equazione può essere trovato in qualsiasi edizione di Data and Computer Communications di William Stallings elencato sotto Nyquist Bandwidth. Nota: autori diversi usano lettere diverse per designare la velocità dei dati, la larghezza di banda, ecc.

2. Come per Nyquist l’equazione si trova in qualsiasi edizione di Data and Computer Communications di William Stallings, questa è elencata sotto Shannon Capacity Formula. Nota: autori diversi usano lettere diverse per designare la velocità dei dati, la larghezza di banda, ecc.

3. Alcuni argomenti della teoria della trasmissione telegrafica (che implicava il limite) sono stati presentati al convegno invernale dell’AIEE, New York, N.Y., 13-17 febbraio 1928. È stato ripubblicato come “Classic Paper” nei Proceedings of the IEEE nel febbraio 2002.

4. “Communications in the Presence of Noise” è stato pubblicato nei Proceedings of the IRE nel gennaio 1949, nove anni dopo essere stato scritto.