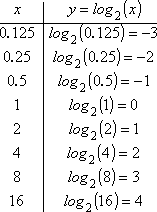Logarithmische Funktionen grafisch darstellen: Einführung

Zurück zum Lektionsindex | Lektionen der Reihe nach bearbeiten | Druckfreundliche Seite

Logarithmische Funktionen grafisch darstellen: Einführung (Seite 1 von 3)

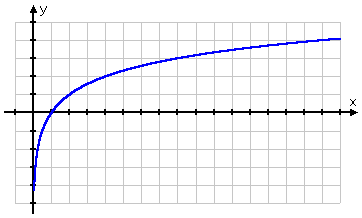
Aufgrund der Natur des Logarithmus haben die meisten Logarithmusgraphen die gleiche Form und sehen ähnlich aus wie ein Quadratwurzelgraph:

y = sqrt(x)	y = log2(x)

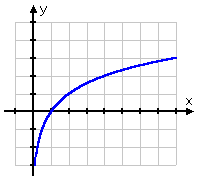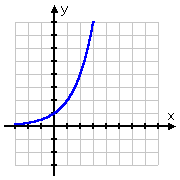
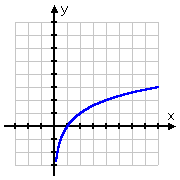
Der Graph der Quadratwurzel beginnt am Punkt (0, 0) und läuft dann nach rechts ab. Der Graph des Logarithmus hingegen verläuft durch (1, 0) und geht nach rechts weg, gleitet aber auch auf der positiven Seite der y-Achse nach unten. Wenn man sich daran erinnert, dass Logarithmen die Inversen von Exponentialen sind, macht diese Form des Logarithmusgraphen absolut Sinn: Der Graph des Logarithmus, der die Inverse des Exponentials ist, wäre einfach die „Umkehrung“ des Graphen des Exponentials:

y = 2x	y = log2(x)
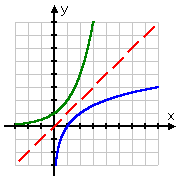
Vergleich der beiden Graphen, Zeigt die Inversionslinie in rot

Es ist ziemlich einfach, Exponentiale grafisch darzustellen. Um z. B. y = 2x zu grafisch darzustellen, setzen Sie einfach einige Werte für x ein, berechnen die entsprechenden y-Werte und zeichnen die Punkte ein. Aber wie kann man Logarithmen grafisch darstellen? Hier gibt es zwei Möglichkeiten. Hier ist die erste: Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved

• Graphen Sie y = log2(x).

Um dies „von Hand“ zu grafisch darzustellen, muss man sich zunächst daran erinnern, dass logs nicht für negatives x oder für x = 0 definiert sind. Wegen dieser Einschränkung des Bereichs (der Eingabewerte) des Logarithmus werde ich nicht einmal versuchen, y-Werte für z. B. x = -3 oder x = 0 zu finden. Stattdessen beginne ich mit x = 1 und arbeite von dort aus, indem ich die Definition des Logarithmus verwende.

Da 20 = 1 ist, ist log2(1) = 0, und (1, 0) befindet sich im Graphen.
Da 21 = 2 ist, dann ist log2(2) = 1, und (2, 1) ist im Graphen.
Da 3 keine Potenz von 2 ist, wird log2(3) ein unschöner Wert sein. Also werde ich mir nicht die Mühe machen, x = 3 grafisch darzustellen.
Da 22 = 4 ist, dann ist log2(4) = 2, und (4, 2) ist im Graphen.
Da 5, 6 und 7 auch keine Potenzen von 2 sind, überspringe ich sie und gehe zu x = 8 über.
Da 23 = 8 ist, dann ist log2(8) = 3, also ist (8, 3) im Graphen.
Die nächste Potenz von 2 ist 16: Da 24 = 16, dann ist log2(16) = 4, und (16, 4) ist im Graphen.
Die nächste 2er-Potenz, x = 32, ist für meinen Geschmack zu groß; ich habe keine Lust, meinen Graphen so breit zu zeichnen, also höre ich bei x = 16 auf.

Das Obige gibt mir den Punkt (1, 0) und einige Punkte rechts daneben, aber was mache ich für x-Werte zwischen 0 und 1? Für dieses Intervall muss ich in Form von negativen Potenzen und Kehrwerten denken. So wie die linke „Hälfte“ der Exponentialfunktion nur wenige grafisch darstellbare Punkte hat (der Rest liegt zu nahe an der x-Achse), so hat auch die untere „Hälfte“ der Logarithmusfunktion nur wenige grafisch darstellbare Punkte, der Rest liegt zu nahe an der y-Achse. Aber ich kann ein paar finden:

Da 2-1 = 1/2 = 0.5, dann ist log2(0.5) = -1, und (0.5, -1) liegt auf dem Graphen.

Da 2-2 = 1/4 = 0.25, dann ist log2(0.25) = -2, und (0.25, -2) liegt auf dem Graphen.

Da 2-3 = 1/8 = 0.125, dann ist log2(0.125) = -3, und (0.125, -3) ist auf dem Graphen.

Die nächste Potenz von 2 (wenn sich x in diese Richtung bewegt) ist 1/16 = 2-4, aber der x-Wert für den Punkt (0.0625, -4) scheint zu klein zu sein, um sich damit zu beschäftigen, also höre ich mit den Punkten auf, die ich bereits gefunden habe.

Das Auflisten dieser Punkte ergibt mein T-Diagramm:
Zeichne ich meine Punkte ein und skizziere dann die Linie (und denke daran, nicht nach links von der y-Achse zu gehen!), erhalte ich dieses Diagramm:

Top | 1 | 2 | 3 | Zurück zum Index Next >>