Departement Informatica en Technologie
Wat is een Turing machine?
Een Turing machine is een hypothetische machine bedacht door de wiskundige Alan Turing in 1936. Ondanks zijn eenvoud kan de machine ELK computeralgoritme simuleren, hoe ingewikkeld het ook is!

Hierboven staat een heel eenvoudige voorstelling van een Turing machine. Het bestaat uit een oneindig lange tape die werkt als het geheugen in een typische computer, of een andere vorm van data-opslag. De vierkantjes op de band zijn meestal leeg aan het begin en kunnen worden beschreven met symbolen. In dit geval kan de machine alleen de symbolen 0 en 1 en ” ” (blanco) verwerken, en wordt dus gezegd dat het een 3-symbolen Turing machine is.
Op elk willekeurig moment heeft de machine een kop die boven een van de vierkanten op de band is geplaatst. Met deze kop kan de machine drie zeer elementaire bewerkingen uitvoeren:
- Leest het symbool op het vakje onder de kop.
- Wijzig het symbool door een nieuw symbool te schrijven of het te wissen.
- Verplaats de band één vakje naar links of rechts, zodat de machine het symbool op een naburig vakje kan lezen en bewerken.
Een eenvoudige demonstratie
Als een triviaal voorbeeld om deze operaties te demonstreren, laten we proberen de symbolen “1 1 0” af te drukken op een aanvankelijk lege tape:

Eerst schrijven we een 1 op het vierkant onder de kop:

Volgende, we verplaatsen de tape naar links met één vierkant:

Nu schrijven we een 1 op het nieuwe vakje onder de kop:

Dan schuiven we de tape weer een vakje naar links:

Tot slot, schrijf een 0 en dat is het!

Een eenvoudig programma
Met de symbolen “1 1 0” op de band, laten we proberen de 1-en om te zetten in 0-en en vice versa. Dit wordt bit inversie genoemd, omdat 1-en en 0-en bits zijn in het binair. Dit kan worden gedaan door de volgende instructies aan de Turing machine door te geven, waarbij gebruik wordt gemaakt van de leesmogelijkheden van de machine om zelf de vervolgbewerkingen te bepalen. Deze instructies vormen een eenvoudig programma.
| Symbool lezen | Schrijf instructie | Verplaats instructie |
|---|---|---|
| None | None | |
| 0 | Write 1 | Verplaats tape naar rechts |
| 1 | Schrijven 0 | Verplaats tape naar rechts |
De machine zal eerst het symbool onder de kop lezen, schrijft een nieuw symbool, verplaatst de band naar links of rechts volgens de instructies, en herhaalt de lees-schrijf-verplaats-volgorde opnieuw.
Laten we eens kijken wat dit programma doet met onze tape vanaf het vorige eindpunt van de instructies:

Het huidige symbool onder de kop is 0, dus we schrijven een 1 en verplaatsen de tape één vakje naar rechts.
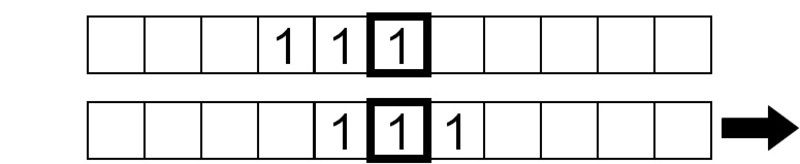
Het symbool dat nu wordt gelezen is 1, dus we schrijven een 0 en schuiven de tape één vakje naar rechts:
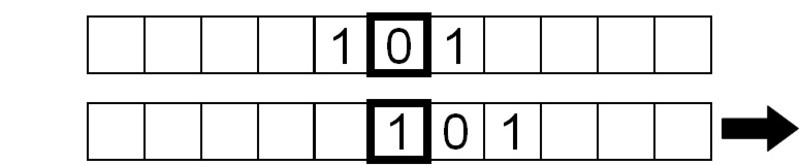
Ook nu is het gelezen symbool een 1, dus we herhalen dezelfde instructies.
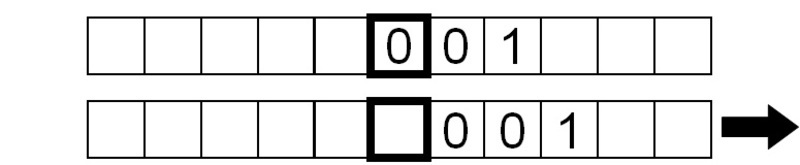
Eindelijk wordt een ‘blanco’ symbool gelezen, dus de machine doet niets anders dan voortdurend het blanco symbool lezen, omdat we haar hebben opgedragen de lees-schrijf-verplaats-reeks te herhalen zonder te stoppen.
In feite is het programma onvolledig. Hoe herhaalt de machine de reeks eindeloos, en hoe stopt de machine met het uitvoeren van het programma?
De machinetoestand
Om het programma te voltooien, moet rekening worden gehouden met de toestandsveranderingen tijdens de uitvoering van het programma op de machine. De volgende cursief gedrukte veranderingen moeten worden toegevoegd aan onze tabel, die nu een toestandstabel kan worden genoemd:
| State | Symbool gelezen | Write instructie | Move instructie | Next state |
|---|---|---|---|---|
| State 0 | Blank | None | None | Stop state |
| 0 | Schrijf 1 | Verplaats de tape naar rechts | Status 0 | |
| 1 | Schrijf 0 | Verplaats de tape naar rechts | State 0 |
We wijzen de vorige set instructies toe aan een machinetoestand, zodat de machine die instructies zal uitvoeren als hij in de gespecificeerde toestand is.
Na elke instructie specificeren we ook een toestand waar de machine naar moet overschakelen. In het voorbeeld wordt de machine teruggestuurd naar zijn oorspronkelijke toestand, toestand 0, om de lees-schrijf-naar-volgorde te herhalen, tenzij een blanco symbool wordt gelezen. Wanneer de machine een blanco symbool leest, wordt de machine naar een stoptoestand geleid en eindigt het programma.
Finite state machines
Ondanks dat het dom lijkt om dit te doen, laten we nu een extra toestand aan ons programma toevoegen die de reeds geïnverteerde bits “1 1 0” terugbrengt van “0 0 1” naar “1 1 0”. Hieronder staat de bijgewerkte tabel, met de wijzigingen in cursief. De Turing machine gedraagt zich nu als een eindige-toestandsmachine met twee toestanden – dit worden drie-symbool, twee-staten Turing machines genoemd.
| State | Symbol read | Write instructie | Move instructie | Next state |
|---|---|---|---|---|
| State 0 | Blank | Write blanco | Verplaats de tape naar links | State 1 |
| 0 | Write 1 | Verplaats de band naar rechts | State 1 | |
| 1 | Write 0 | Verplaats de tape naar rechts | State 0 | |
| State 1 | Blank | Schrijf blanco | Verplaats de tape naar rechts | State Stop |
| 0 | Schrijf 1 | Verplaats de tape naar links | State 1 | |
| 1 | Write 0 | Verplaats de tape naar links | State 1 |
Voor de schrijfinstructie, “Geen” is veranderd in “Schrijf leeg” omwille van de uniformiteit (zodat alleen naar de symbolen van de machine wordt verwezen), en opgemerkt moet worden dat ze gelijkwaardig zijn.
In plaats van een toestandstabel kan het programma ook worden weergegeven met een toestandsdiagram:
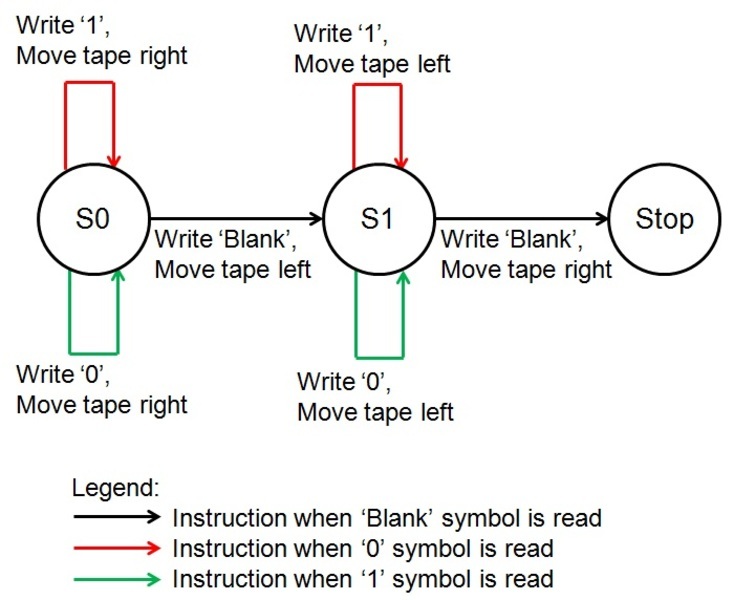
Van waar het programma voorheen was, in plaats van niets te doen en te stoppen nadat de machine een leeg symbool tegenkomt, geven we haar de opdracht de band naar links te verplaatsen alvorens over te gaan naar toestand 1 waar ze het bitinversieproces omkeert.
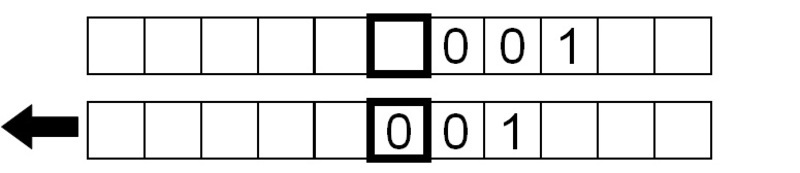
Volgende keer keren we de bits weer om, deze keer door de tape naar links te bewegen in plaats van naar rechts.
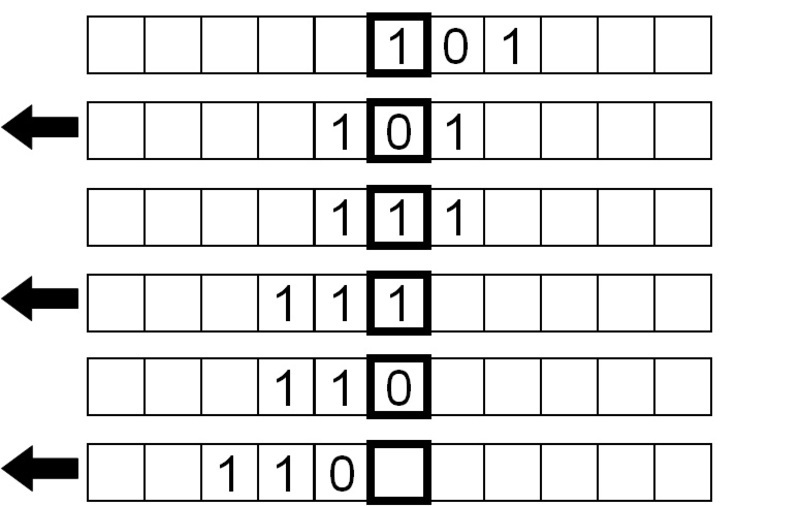
Eindelijk wordt er een blanco symbool gelezen, dus we schuiven de tape naar rechts om terug te keren naar waar we begonnen, en stoppen het programma.

Met de introductie van meer toestanden in ons programma, kunnen we de Turing machine opdragen complexere functies uit te voeren, en daarmee elk algoritme uitvoeren dat een moderne computer kan uitvoeren.
In deel twee, laten we leren over LEDs, GPIO pinnen, weerstanden, en python, voordat we beginnen met het bouwen van onze Turing machine!