Hoe basis te begrijpen (lineaire algebra)

Bij het onderwijzen van lineaire algebra, wordt het concept van een basis vaak over het hoofd gezien. Mijn bijlesleerlingen konden lineaire onafhankelijkheid en bereik begrijpen, maar ze zagen de basis zoals je een UFO zou kunnen zien: verwarrend en vreemd. En dat is niet goed, want de basis fungeert als uitgangspunt voor een groot deel van de lineaire algebra.

We hebben altijd een beginpunt nodig, een fundament om al het andere op te bouwen. Woorden kunnen niet worden geschreven zonder de basis van een alfabet. Oude beschavingen geloofden dat het universum was gevormd uit 4 klassieke elementen – water, aarde, vuur en lucht (lang geleden…). En vectorruimten, het natuurlijke huis van de lineaire algebra, hebben de basis als hun fundament.

Ik ga de basis conceptueel uitleggen aan de hand van een analogie met schilderen. Deze analogie is in twee eerdere artikelen gebruikt om twee andere concepten uit de lineaire algebra uit te leggen: lineaire onafhankelijkheid/afhankelijkheid en overspanning. Ik raad aan die artikelen eerst te lezen, omdat beide begrippen later terugkomen.

De basis van verfkleuren

In plaats van wiskunde te doen, stel je voor dat je een schilder bent, klaar om een meesterwerk op je doek te schilderen. Eerst moet u verf kopen. Hoeveel kleuren moet u kopen?

Het is natuurlijk een slecht idee om een schilderij te maken door naar Home Depot te rijden en voor alle duizenden kleuren die ze hebben, telkens één blik verf te kopen. Je hebt geen dertig verschillende tinten blauw nodig, van Azure Blue, tot Mountain Blue, helemaal tot Victory Blue (idee: maak een verf die “Defeat Blue” heet). Je hoeft alleen maar blauwe verf te kopen en een paar andere kleuren.

Als je een gierige schilder bent, zou je zelfs kunnen zeggen dat je maar 5 kleuren hoeft te kopen om een schilderij te maken: rood, geel, blauw, wit, en zwart. Natuurlijk, groen zou mooi zijn, en roze zou cool zijn, maar je hoeft geen roze en groene verf te kopen. Je kunt immers ook rode en witte verf combineren om roze te maken, of gele en blauwe verf om groen te maken.

Rood, geel, blauw, wit en zwart zijn de minimale set kleuren die je nodig hebt om een andere kleur te maken. We zouden kunnen zeggen dat deze 5 kleuren een basis vormen voor het hele kleurenspectrum.

Omdat je elke andere kleur kunt maken met mengsels van deze vijf kleuren, zouden we kunnen zeggen dat deze vijf kleuren de verzameling van alle kleuren omvatten. Bovendien is elke kleur in de verzameling noodzakelijk: je hebt witte verf nodig omdat geen enkele hoeveelheid gele, rode, zwarte of blauwe verf gemengd met elkaar ooit witte verf zal opleveren. Met andere woorden, rood, geel, blauw, wit en zwart zijn onafhankelijk van elkaar.

Laten we je verzameling verven je palet noemen. Wil je palet een basis vormen voor alle kleuren, dan moeten twee voorwaarden waar zijn:

1. Het palet omspant de verzameling van alle kleuren.
2. Alle kleuren in het palet zijn onafhankelijk van elkaar.

We hebben net gezien dat rood, geel, blauw, wit, en zwart aan beide voorwaarden voldoen. Daarentegen zijn hier voorbeelden van paletten die geen basis zijn:

• Rood, blauw, wit. Dit is in strijd met voorwaarde 1. Deze verzameling omvat niet alle kleuren. Veel kleuren zoals geel of groen zijn onmogelijk te maken met kleuren uit deze verzameling.
• Rood, oranje, geel, groen, blauw, paars, wit, zwart. Dit is in strijd met voorwaarde 2. Deze kleuren omvatten zeker alle kleuren, maar ze zijn niet onafhankelijk. Paars is een combinatie van rood en blauw, groen een combinatie van geel en blauw, enzovoort.

De basis van een vectorruimte

Vectorruimten zijn abstracter dan schilderijen, maar ze gebruiken de basis op dezelfde manier. Een vectorruimte is een verzameling vectoren waarbij je vectoren kunt optellen en schalen. Bijvoorbeeld, het 2-D vlak (ook gekend als R²) is een vectorruimte. Het is de verzameling van alle “2-dimensionale” vectoren, die je kunt beschouwen als vectoren met een x-coördinaat en een y-coördinaat.

Net zoals we een basis hebben gemaakt voor de verzameling van alle kleuren, kunnen we een verzameling vectoren maken die een basis vormen van R². De vereisten voor de basis zijn bijna dezelfde als die voor de kleuren.

Basis: Een verzameling van n vectoren, {v₁, v₂,… vₙ}, is een basis van een of andere ruimte S als deze twee voorwaarden waar zijn:

1. {v₁, v₂, …vₙ} zijn lineair onafhankelijk.
2. {v₁, v₂,…vₙ} overspannen de verzameling S. Met andere woorden, Span{v₁,v₂,…vₙ}=S

Neem bijvoorbeeld de vectoren (0,1) en (1,0), hieronder in groen gegraveerd. Deze vectoren zijn lineair onafhankelijk, omdat er geen manier is om (0,1) in (1,0) te schalen. Bovendien beslaan deze twee vectoren het gehele 2D-vlak, omdat je elk punt in de 2D-ruimte kunt herschrijven als een lineaire combinatie van (0,1) en (1,0):

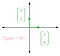
(0,1) en (1,0) vormen dus een basis van R² (Deze specifieke basis van (0,1) en (1,0) wordt de standaardbasis genoemd). Dit is echter niet de enige basis van R² die mogelijk is. Kijk eens naar de vectoren (1,1) en (-1,1), hieronder grafisch weergegeven. De roze vectoren stellen een paar verschillende lineaire combinaties voor:

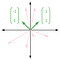
Deze twee vectoren zijn ook lineair onafhankelijk, aangezien je de ene vector niet in de andere kunt schalen. Uit de roze lineaire combinaties blijkt ook dat (1,1) en (-1,1) geheel R² omspannen. Daarom vormen (1,1) en (-1,1) een andere basis voor R².

Dit is een punt waarop vectorruimten heel anders zijn dan de verf-analogie. Met verfkleuren hebben we eigenlijk alleen de basis van geel, blauw, rood, zwart en wit. Maar in de wereld van de vectorruimten kan elke ruimte kiezen uit een oneindig aantal basissen. In het algemeen is een basis de kleinst mogelijke verzameling vectoren die een ruimte kan omvatten. Het is het vector-equivalent van gierig zijn met verf en alleen de minimaal benodigde kleuren kopen.

De basis helpt ons ook de onderliggende structuur van een vectorruimte te achterhalen. We weten bijvoorbeeld dat elke basis van R² uit precies twee vectoren zal bestaan, zoals de twee bases die we eerder vonden. In het algemeen:

• Voor een bepaalde ruimte S hebben alle basen van S evenveel vectoren. Dit is voor het eerst bewezen door Georg Hamel. Als een basis voor S uit 4 vectoren bestaat, dan bestaat elke basis voor S uit 4 vectoren.
• Een basis voor een Rⁿ ruimte bestaat uit n vectoren. Elke basis voor R³ (3-dimensionale ruimte) bestaat uit 3 vectoren. Een basis voor R⁵ (5-dimensionale ruimte, vraag maar niet) bestaat uit 5 vectoren.

Waarom de basis belangrijk is (Lineaire Transformaties)

Op zichzelf heeft de basis niet veel invloed. Laten we echter kort bespreken waarom de basis zo belangrijk is voor lineaire algebra.

We kunnen een vectorruimte transformeren, waarbij “transformeren” betekent dat we de ruimte uitrekken, omdraaien of roteren. Bij het werken met lineaire algebra is het transformeren van een vectorruimte net zo gewoon als ademhalen. Stel dat ik de grafiek A wil transformeren in grafiek B:

Elke grafiek heeft zijn eigen basis (de roze en blauwe vectoren). Belangrijk is dat zowel grafiek A als grafiek B gewoon twee verschillende manieren zijn om precies dezelfde ruimte weer te geven met behulp van verschillende bases. Het is alsof je hetzelfde boek leest, maar dan in twee verschillende talen, zoals Spaans en Frans.

Het verschuiven van grafiek A naar grafiek B wordt een lineaire transformatie van de grafiek genoemd. Een lineaire transformatie werkt als een vertaler: Het neemt elk punt in grafiek B en verplaatst het naar elk corresponderend punt in grafiek A. Het neemt het Franse woord en verplaatst het naar het Spaans. We komen nu echter in de wereld van lineaire transformaties, en dat kan een andere keer worden uitgelegd.

Conclusie

We hebben nu een beter begrip van drie lineaire algebra-concepten: basis, lineaire onafhankelijkheid/afhankelijkheid, en spanwijdte. Deze concepten zijn fundamenteel voor lineaire algebra. Lineaire onafhankelijkheid/afhankelijkheid vertelt je welke vectoren noodzakelijk zijn in een verzameling vectoren. Spanwijdte vertelt je alle mogelijke combinaties van vectoren die je kunt maken. En de basis vertelt je de kleinste verzameling vectoren die nodig is om een vectorruimte te overspannen, en dus de structuur van die ruimte.

Beheersing van deze concepten geeft je de basis die je nodig hebt voor een concreet begrip van lineaire algebra. Immers, een huis kan niet staan op een wankele basis, en we kunnen lineaire algebra niet begrijpen zonder een basis. Bedankt voor het lezen!