Maximum waarde van een geheel getal: Java Vs C vs Python | Baeldung on Computer Science

Inleiding

In Data Science, als we het over gehele getallen hebben, verwijzen we naar een datatype dat een bepaald bereik van wiskundige gehele getallen weergeeft. We weten dat wiskundige gehele getallen geen bovengrens hebben, maar dit kan een probleem zijn in termen van geheugengrootte, waardoor bijna elke computerarchitectuur gedwongen is dit datatype te beperken.

Dus, dat is de vraag die we vandaag proberen te stellen: “Wat is de maximale integer-waarde die we op een bepaalde machine kunnen representeren?”

Uitleg van het probleem

Wel, er is geen uniek antwoord op deze vraag, omdat er veel factoren zijn die het antwoord beïnvloeden. De belangrijkste zijn:

Platformbits
Gebruikte taal
Getekende of niet-getekende versies

In de informatica is de meest gebruikelijke representatie van gehele getallen door een groep binaire cijfers (bits), opgeslagen als een binair getallenstelsel. De volgorde van de geheugenbytes varieert – met bits, kunnen we gehele getallen coderen.

We kunnen de verschillen in dit eenvoudige voorbeeld zien: met bits, kunnen we gehele getallen coderen van tot of van $- 2^{n-1}$ tot $2^{n-1} - 1$ .

In de regel wordt de integer grootte gedefinieerd door de machine-architectuur, maar sommige computertalen definiëren integer groottes ook onafhankelijk. Verschillende CPU’s ondersteunen verschillende datatypes, gebaseerd op hun eigen platform. Typisch ondersteunen ze allemaal zowel signed als unsigned types, maar alleen van een beperkte en vaste set breedtes, meestal 8, 16, 32 en 64 bits.

Sommige talen definiëren twee of meer soorten integer datatypes, een kleinere om geheugen te sparen en minder opslagruimte in beslag te nemen, en een grotere om het ondersteunde bereik te verbeteren.

Een ander ding om in gedachten te houden is de Word Size (ook wel Word Length genoemd) van het platform.

In de informatica is een woord de eenheid van gegevens die wordt gebruikt door een bepaald processorontwerp, een stuk gegevens van vaste grootte dat als eenheid wordt behandeld door de hardware van de processor. Als we het over woordgrootte hebben, hebben we het over het aantal bits in een woord en dit is een cruciaal kenmerk van elke specifieke computerarchitectuur en processorontwerp.

De huidige architecturen hebben meestal een woordgrootte van 64 bits, maar er zijn er ook met 32 bits.

Tijd voor de antwoorden

In dit gedeelte zullen we onze vragen beantwoorden, beginnend bij de oude vriend C tot het relatief nieuwe Python, langs het altijdgroene Java. Laten we beginnen.

3.1. C

De C taal is ontworpen in 1972, met het doel om op verschillende machinetypes op dezelfde manier te werken. Het bepaalt dus niet direct een bereik voor het gehele gegevenstype, omdat dat afhankelijk is van de machine-architectuur.

Hoewel, C kent twee soorten gehele getallen; kort en lang.

Een kort geheel getal is, tenminste, 16 bits. Dus, op een 16-bits machine, valt het samen met het lange gehele getal formaat. Het korte gehele getal loopt van -32.767 tot 32.767 voor de getekende versie en van 0 tot 65.535 voor de niet-getekende. Nou, het is vreemd, maar het lijkt erop dat we voor de ondertekende versie een getal missen. Dat is eenvoudig te verklaren: omdat we één bit nodig hebben voor het teken!

Als we op een 64-bit systeem draaien, kunnen we eenvoudig berekenen dat het lange formaat een $2^{64-1}$ waarde kan bereiken, wat overeenkomt met 18,446,744,073,709,551,615 voor het unsigned datatype en varieert van -9.223.372.036.854.775.807 tot 9.223.372.036.854.775.807 in de signed versie.

Voor de volledigheid gaan we nog even in op het lange lange integer datatype. Het lange lange formaat is niet beschikbaar in C, maar alleen in de C99-versie. Het heeft dubbel zoveel geheugencapaciteit als een lang gegevenstype, maar het wordt uiteraard niet ondersteund door compilers die de vorige C-standaard vereisen. Met het lange datatype kunnen we een enorme $2^{64-1}$ bereiken als we het op een 32-bit machine of hoger draaien.

3.2. Java

Als we het over Java hebben, moeten we onthouden dat het werkt via een virtuele machine. Dat bespaart ons alle variabiliteit die voor de C-taal is uitgelegd.

Java ondersteunt alleen getekende versies van gehele getallen. Dat zijn:

byte (8 bits)
short (16 bits)
int (32 bits)
long (64 bits)

Dus met het lange integer-formaat kunnen we $2^{64-1}$ bereiken zoals met C op een 64-bits machine, maar, dit keer, op elke machine-architectuur.

Maar met wat bitmanipulatie kunnen we ook niet-ondertekende versies krijgen, dankzij het char formaat. Dat is een 16-bit formaat, dus het unsigned integer formaat kan oplopen tot 65.535.

Maar met Java kunnen we verder gaan met een kleine hack, zodat we zeer grote integer getallen kunnen representeren via de BigInteger klasse bibliotheek. Deze bibliotheek combineert arrays van kleinere variabelen om enorme getallen op te bouwen. De enige limiet is het fysieke geheugen, zodat we een enorm, maar nog steeds beperkt, bereik van gehele getallen kunnen representeren.

Met 1 kilobyte geheugen kunnen we bijvoorbeeld gehele getallen tot 2.466 cijfers lang bereiken!

3.3. Python

Python ondersteunt direct arbitraire precisie gehele getallen, ook wel oneindige precisie gehele getallen of bignums genoemd, als een top-level construct.

Dit betekent, net als bij Java BigInteger, dat we zoveel geheugen gebruiken als nodig is voor een arbitrair groot geheel getal. Dus, in termen van programmeertaal, is deze vraag helemaal niet van toepassing op Python, want het gewone integer type is, theoretisch onbegrensd.

Wat niet onbegrensd is, is de huidige woordgrootte van de interpreter, die in de meeste gevallen hetzelfde is als de woordgrootte van de machine. Die informatie is in Python beschikbaar als sys.maxsize, en het is de grootte van de grootst mogelijke lijst of in-memory sequence, die overeenkomt met de maximale waarde die door een ondertekend woord kan worden gerepresenteerd.

Op een 64-bit machine komt dat overeen met $2^{64-1}$ = 9,223,372,036,854,775,807.

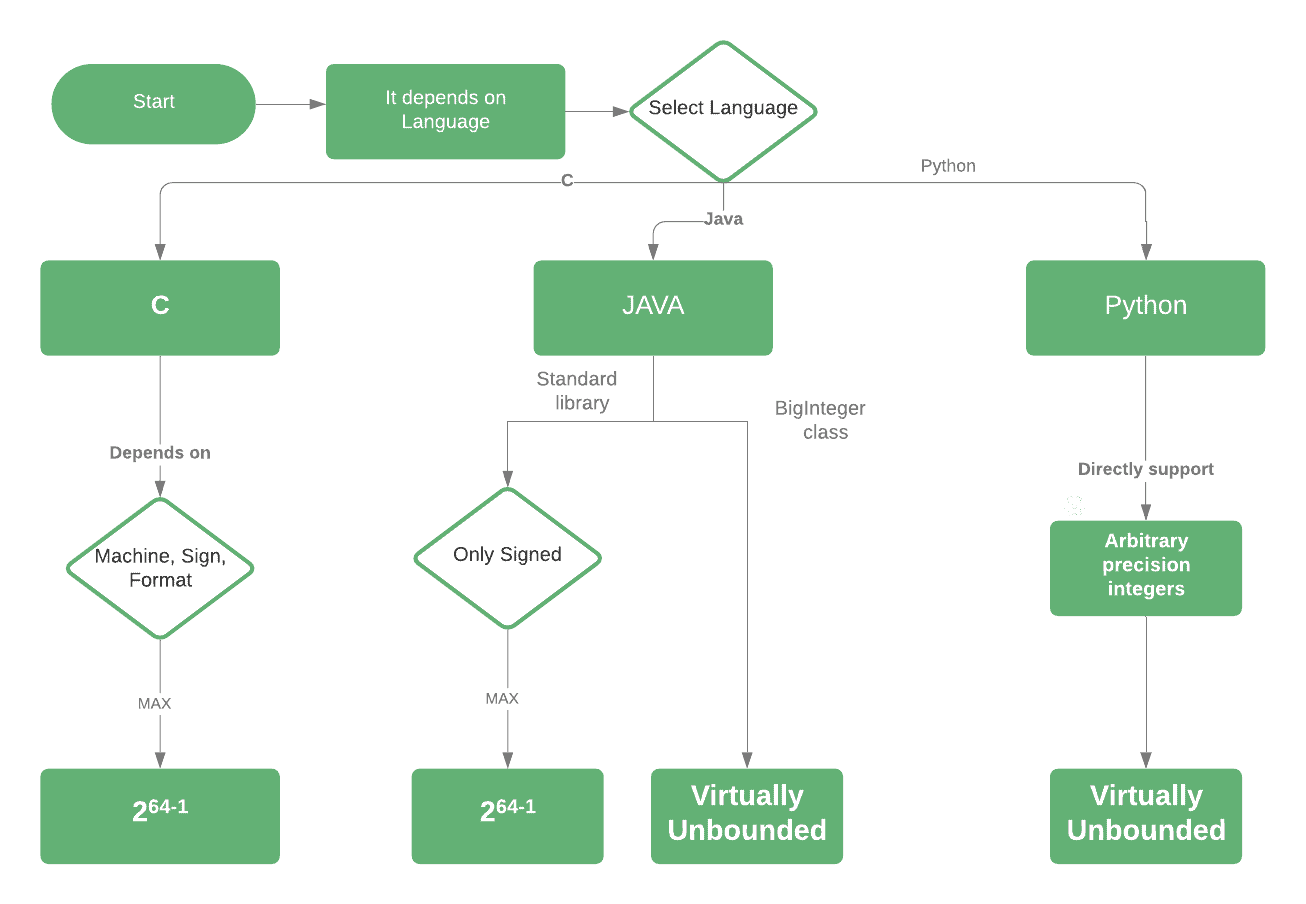
Stroomdiagram

Laten we eens kijken naar een stroomdiagram om samen te vatten wat we tot nu toe hebben gezien:

Echte code voor elke taal

Hier is wat echte code om direct te controleren wat we tot nu toe hebben besproken. De code demonstreert de maximum en minimum waarden van gehele getallen in elke taal.

Omdat deze waarden niet bestaan in Python, laat de code zien hoe de woordgrootte van de huidige interpreter wordt weergegeven.

5.1. C Code

#include<bits/stdc++.h>int main() { printf("%d\n", INT_MAX); printf("%d", INT_MIN); return 0; }

5.2. Java Code

public class Test { public static void main(String args) { System.out.println(Integer.MIN_VALUE); System.out.println(Integer.MAX_VALUE); }}

5.3. Python Code

import platformplatform.architecture()import syssys.maxsize

Conclusie

In dit artikel hebben we de verschillen behandeld tussen deze drie toptalen over het maximaal mogelijke gehele getal. We hebben ook laten zien dat deze vraag in sommige situaties niet van toepassing is.

Hoewel men altijd de best passende in zijn situatie moet gebruiken om geheugengebruik en systeemvertraging te voorkomen.

Maximum Value of an Integer: Java Vs C vs Python