SAT / ACT Prep Online Guides and Tips

Als je trigonometrie of wiskunde studeert, of als je er klaar voor bent, moet je vertrouwd raken met de eenheidscirkel. De eenheidscirkel is een essentieel instrument dat wordt gebruikt om de sinus, cosinus en tangens van een hoek op te lossen. Maar hoe werkt het? En welke informatie moet je weten om hem te kunnen gebruiken?

In dit artikel leggen we uit wat de eenheidscirkel is en waarom je hem moet kennen. We geven je ook drie tips om je te helpen onthouden hoe je de eenheidscirkel moet gebruiken.

Feature Image: Gustavb/Wikimedia

De eenheidscirkel: Een basisinleiding

De eenheidscirkel is een cirkel met een straal van 1. Dit betekent dat voor elke rechte lijn getrokken van het middelpunt van de cirkel naar elk punt langs de rand van de cirkel, de lengte van die lijn altijd gelijk is aan 1. (Dit betekent ook dat de diameter van de cirkel gelijk is aan 2, aangezien de diameter gelijk is aan tweemaal de lengte van de straal)

De eenheidscirkel is een cirkel met een straal van 1. Dit betekent dat voor elke rechte lijn getrokken van het middelpunt van de cirkel naar elk punt langs de rand van de cirkel, de lengte van die lijn altijd gelijk is aan 1.)

Typisch is het middelpunt van de eenheidscirkel waar de x-as en de y-as elkaar snijden, of op de coördinaten (0, 0):

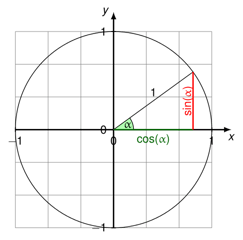
De eenheidscirkel, of trigcirkel zoals hij ook wel wordt genoemd, is handig om te weten omdat we er gemakkelijk de cosinus, sinus en tangens mee kunnen berekenen van elke hoek tussen 0° en 360° (of 0 en 2π radialen).

Zoals je in bovenstaand diagram kunt zien, creëer je een rechthoekige driehoek door een straal te tekenen in een willekeurige hoek (in het plaatje aangegeven met ∝). In deze driehoek is de cosinus de horizontale lijn, en de sinus de verticale lijn. Met andere woorden, cosinus = x-coördinaat, en sinus = y-coördinaat. (De langste lijn van de driehoek, of hypotenusa, is de straal en dus gelijk aan 1.)

Waarom is dit allemaal van belang? Je kunt de lengtes van de zijden van een driehoek bepalen met de stelling van Pythagoras, ofwel $a^2+b^2=c^2$ (waarbij a en b de lengtes van de zijden van de driehoek zijn, en c de lengte van de schuine zijde)

We weten dat de cosinus van een hoek gelijk is aan de lengte van de horizontale lijn, de sinus gelijk is aan de lengte van de verticale lijn, en de schuine zijde gelijk is aan 1. Daarom kunnen we zeggen dat de formule voor een willekeurige rechthoekige driehoek in de eenheidscirkel als volgt luidt:

$$$$$$$$$$$$$$$$$$$$$$$$$$$$

Omdat $1^2=1$ is, kunnen we deze vergelijking als volgt vereenvoudigen:

$\cos^2θ+\sin^2θ=1$

Bewustzijn dat deze waarden negatief kunnen zijn, afhankelijk van de gevormde hoek en in welk kwadrant de x- en y-coördinaten vallen (ik leg dit later nog nader uit).

Hier volgt een overzicht van alle grote hoeken in graden en radialen op de eenheidscirkel:

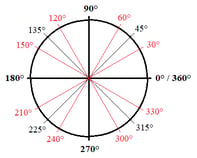
Unit Circle – Degrees

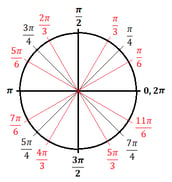
Unit Circle – Radians

Maar wat als er geen driehoek gevormd is? Laten we eens kijken wat er gebeurt als de hoek 0° is, waardoor een horizontale rechte lijn langs de x-as ontstaat:

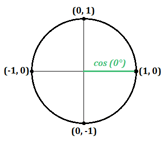
Op deze lijn is de x-coördinaat gelijk aan 1 en de y-coördinaat gelijk aan 0. We weten dat de cosinus gelijk is aan de x-coördinaat, en de sinus gelijk aan de y-coördinaat, dus kunnen we dit schrijven:

• $\cos0°=1$
• $\sin0°=0$

Wat als de hoek 90° is en een perfect verticale lijn langs de y-as vormt?

Hier zien we dat de x-coördinaat gelijk is aan 0 en de y-coördinaat gelijk aan 1. Dit geeft ons de volgende waarden voor sinus en cosinus:

• $\cos90°=0$
• $\sin90°=1$

Deze slogan is zeker van toepassing als je geen liefhebber van wiskunde bent.

Waarom moet je de eenheidscirkel kennen

Zoals gezegd is de eenheidscirkel nuttig omdat we er gemakkelijk de sinus, cosinus of tangens van elke graad of radiaal mee kunnen oplossen. Het is vooral nuttig om de eenheidscirkelgrafiek te kennen als je bepaalde trigo-waarden moet oplossen voor wiskundehuiswerk of als je je voorbereidt op een studie calculus.

Maar hoe kan kennis van de eenheidscirkel je precies helpen? Stel, je krijgt het volgende probleem voor een wiskundetoets – en je mag geen rekenmachine gebruiken om het op te lossen:

$_sin30°$

Waar moet je beginnen? Laten we nog eens naar de eenheidscirkeldiagram kijken-dit keer met alle grote hoeken (zowel in graden als radialen) en hun bijbehorende coördinaten:

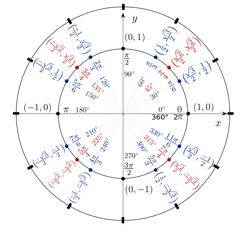Jim.belk/Wikimedia

Wees niet overweldigd! Denk eraan, alles wat je oplost is $40sin30°$. Als we naar deze grafiek kijken, zien we dat de y-coördinaat gelijk is aan $1/2$ op 30°. En omdat de y-coördinaat gelijk is aan de sinus, is ons antwoord als volgt:

$\sin30°=1/2$

Maar wat als je een probleem krijgt dat radialen gebruikt in plaats van graden? Het oplossen gaat nog steeds op dezelfde manier. Stel dat je bijvoorbeeld een probleem krijgt dat er als volgt uitziet:

$\cos{{3π}/4}$

Wederom kunnen we met behulp van de grafiek hierboven zien dat de x-coördinaat (of cosinus) voor ${3π}/4$ (die gelijk is aan 135°) $-{√2}/2$ is. Zo zou ons antwoord op dit probleem er dan uitzien:

$\cos({3π}/4)=-{√2}/2$

Dit is allemaal vrij eenvoudig als je de eenheidscirkeldiagram hierboven als referentie kunt gebruiken. Maar meestal (zo niet altijd) is dat niet het geval en wordt er van je verwacht dat je dit soort wiskundevragen alleen met je hersenen beantwoordt.

Dus hoe kun je de eenheidscirkel onthouden? Lees verder voor onze beste tips!

Hoe onthoud je de eenheidscirkel: 3 essentiële tips

In dit gedeelte geven we je onze beste tips voor het onthouden van de trigcirkel, zodat je hem met gemak kunt gebruiken voor elk wiskundeprobleem waarvoor hij nodig is.

Ik zou niet aanraden om de eenheidscirkel met post-its te oefenen, maar ach, het is een begin.

#1: Onthoud veel voorkomende hoeken en coördinaten

Om de eenheidscirkel effectief te kunnen gebruiken, moet je de meest voorkomende hoeken (in zowel graden als radialen) onthouden, evenals hun corresponderende x- en y-coördinaten.

Het diagram hierboven is een handige eenheidscirkeldiagram om naar te kijken, omdat het alle belangrijke hoeken in zowel graden als radialen bevat, naast hun corresponderende coördinaatpunten langs de x- en y-as.

Hier is een grafiek die deze zelfde informatie in tabelvorm weergeeft:

Angle (Graden)	Angle (Radialen)	Coordinaten van punt op cirkel	0° / 360°	0 / 2π	(1., 0)
30°	$π/6$	$({√3}/2, 1/2)$
45°	$π/4$	$({√2}/2, {√2}/2)$
60°	$π/3$	$(1/2,{√3}/2)$
90°	$π/2$	(0, 1)
120°	${2π}/3$	$(-1/2, {√3}/2)$
135°	${3π}/4$	$(-{√2}/2, {√2}/2)$
150°	${5π}/6$	$(-{√3}/2, 1/2)$
180°	π	(-1, 0)
210°	${7}/6$	$(-{√3}/2, -1/2)$
225°	${5π}/4$	$(-{√2}/2, -{√2}/2)$
240°	${4π}/3$	$(-1/2, -{√3}/2)$
270°	${3π}/2$	(0, -1)
300°	${5π}/3$	$(1/2, -{√3}/2)$
315°	${7π}/4$	$({√2}/2, -{√2}/2)$
330°	${11π}/6$	$({√3}/2, -1/2)$

Nu, je mag best proberen al deze coördinaten en hoeken uit je hoofd te leren, maar dit is wel erg veel om te onthouden.

Gelukkig is er een trucje dat je kunt gebruiken om de belangrijkste delen van de eenheidscirkel te onthouden.

Kijk naar de coördinaten hierboven en je ziet een duidelijk patroon: alle punten (behalve die op 0°, 90°, 270° en 360°) wisselen tussen slechts drie waarden (positief of negatief):

• $1/2$
• ${√2}/2$
• ${√3}/2$

Elke waarde komt overeen met een korte, middellange of lange lijn voor zowel cosinus als sinus:

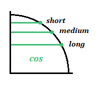
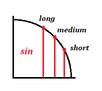
Hier ziet u wat deze lengtes betekenen:

• Korte horizontale of verticale lijn = $1/2$
• Middelgrote horizontale of verticale lijn = ${√2}/2$
• Lange horizontale of verticale lijn = ${√3}/2$

Bijv. als je ${√cos{π/3}$ probeert op te lossen, moet je meteen weten dat deze hoek (die gelijk is aan 60°) een korte horizontale lijn op de eenheidscirkel aangeeft. Daarom moet zijn overeenkomstige x-coördinaat gelijk zijn aan $1/2$ (een positieve waarde, want $π/3$ creëert een punt in het eerste kwadrant van het coordinatenstelsel).

Ter slotte, hoewel het nuttig is om alle hoeken in bovenstaande tabel uit het hoofd te leren, merk op dat verreweg de belangrijkste hoeken om te onthouden de volgende zijn:

• 30° / $π/6$
• 45° / $π/4$
• 60° / $π/3$

Behandel je negatieven en positieven zoals je kabels zou behandelen die je kunnen doden als ze niet goed zijn aangesloten.

#2: Leer wat negatief en wat positief is

Het is belangrijk om positieve en negatieve x- en y-coördinaten te kunnen onderscheiden, zodat je de juiste waarde vindt voor een trigoprobleem. Ter herinnering: of een coördinaat op de eenheidscirkel positief of negatief is, hangt af van in welk kwadrant (I, II, III of IV) het punt valt:

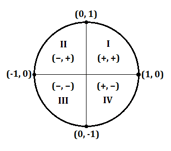
Hier volgt een grafiek die laat zien of een coördinaat positief of negatief is op basis van het kwadrant waarin een bepaalde hoek (in graden of radialen) valt:

Kwadrant	X-Coordinaat (Cosinus)	Y-Coördinaat (sinus)
I	+	+
II	–	+
III	–	–
IV	+	–

Bij wijze van voorbeeld, stel dat je op een wiskundetoets het volgende probleem krijgt:

$210°$

Voordat je zelfs maar probeert het op te lossen, moet je in staat zijn te herkennen dat het antwoord een negatief getal zal zijn omdat de hoek 210° in kwadrant III valt (waar x-coördinaten altijd negatief zijn).

Nu, met behulp van de truc die we in tip 1 hebben geleerd, kun je uitrekenen dat een hoek van 210° een lange horizontale lijn oplevert. Ons antwoord is daarom als volgt:

$\cos210°=-{√3}/2$

#3: Weet hoe je de raaklijn oplost

Ten slotte is het essentieel om te weten hoe je al deze informatie over de goniometrische cirkel en sinus en cosinus moet gebruiken om de raaklijn van een hoek op te kunnen lossen.

In trigonometrie vind je de tangens van een hoek θ (in graden of radialen) door eenvoudigweg de sinus door de cosinus te delen:

$\tanθ={\sinθ}/{\cosθ}$

Stel bijvoorbeeld dat je dit probleem probeert op te lossen:

$300°$

De eerste stap is het opstellen van een vergelijking in termen van sinus en cosinus:

$\tan300°={\sin300°}/{\cos300°}$

Nu, om de tangens op te lossen, moeten we de sinus en cosinus van 300° vinden. Je moet snel kunnen herkennen dat de hoek 300° in het vierde kwadrant valt, wat betekent dat de cosinus, of x-coördinaat, positief zal zijn, en de sinus, of y-coördinaat, negatief zal zijn.

Je moet ook meteen weten dat de hoek 300° een korte horizontale lijn en een lange verticale lijn oplevert. Daarom zal de cosinus (de horizontale lijn) gelijk zijn aan $1/2$, en de sinus (de verticale lijn) aan $-{√3}/2$ (een negatieve y-waarde, want dit punt ligt in kwadrant IV).

Nu, om de tangens te vinden, hoef je alleen maar in te pluggen en op te lossen:

$$$300°={-{√3}/2}/{1/2}$

$$300°=-√3$

Tijd om je wiskunde-vaardigheden te spinnen!

Unit Circle Practice Question Set

Nu je weet hoe de eenheidscirkel eruit ziet en hoe je hem moet gebruiken, laten we eens testen wat je geleerd hebt met een paar oefenopgaven.

Ontwerpen

1. $:sin45°$
2. $:cos240°$
3. $:cos{5π}/3$
4. $:tan{2π}/3$

Antwoorden

1. ${√2}/2$
2. $-1/2$
3. $1/2$
4. $-√3$

Antwoorden Uitleg

#1: $-√3$

Bij dit probleem zijn er twee stukjes informatie die je meteen zou moeten kunnen identificeren:

• Het antwoord zal positief zijn, aangezien de hoek 45° in kwadrant I ligt, en de sinus van een hoek gelijk is aan de y-coördinaat

• De hoek 45° geeft een verticale lijn van gemiddelde lengte (voor sinus)

Omdat 45° een positieve, middellange lijn aangeeft, is het juiste antwoord ${√2}/2$.

Als je niet zeker weet hoe je dit moet uitrekenen, teken dan een diagram om te bepalen of de lengte van de lijn kort, middellang of lang zal zijn.

#2: $240°$

Net als bij opgave #1 hierboven zijn er twee stukjes informatie die je snel zou moeten kunnen begrijpen bij deze opgave:

• Het antwoord zal negatief zijn, aangezien de hoek 240° in kwadrant III ligt, en de cosinus van een hoek gelijk is aan de x-coördinaat

• De hoek 240° levert een korte horizontale lijn op (voor cosinus)

Omdat 240° een negatieve, korte lijn aangeeft, is het juiste antwoord $-1/2$.

#3: $\cos{5π}/3$

In tegenstelling tot de problemen hierboven wordt hier gebruik gemaakt van radialen in plaats van graden. Hoewel het probleem daardoor lastiger op te lossen lijkt, worden in werkelijkheid dezelfde basisstappen gebruikt als bij de andere twee problemen.

Je moet allereerst weten dat de hoek ${5π}/3$ in kwadrant IV ligt, dus de x-coördinaat, of cosinus, zal een positief getal zijn. Je zou ook moeten kunnen zien dat ${5π}/3$ een korte horizontale lijn vormt.

Dit geeft je genoeg informatie om te bepalen dat het antwoord $1/2$ is.

#4: $\tan{2π}/3$

Dit probleem gaat over raaklijn in plaats van sinus of cosinus, wat betekent dat het iets meer wiskunde van onze kant vereist. Herinner je eerst de basisformule voor het vinden van de tangens:

$\tan θ={\sin θ}/{\cos θ}$

Nu nemen we de graad die we hebben gekregen -${2π}/3$ – en voegen die in deze vergelijking:

$2π}/3={2π}/3}/{2π}/3$

Je zou nu in staat moeten zijn om de sinus en cosinus afzonderlijk op te lossen met wat je hebt onthouden over de eenheidscirkel. Omdat de hoek ${2π}/3$ in kwadrant II ligt, zal de x-coördinaat (of cosinus) negatief zijn, en de y-coördinaat (of sinus) positief.

Daarna moet je op basis van de hoek alleen al kunnen bepalen dat de horizontale lijn een korte lijn is, en de verticale lijn een lange lijn. Dit betekent dat de cosinus gelijk is aan $-1/2$, en de sinus gelijk is aan ${√3}/2$.

Nu we deze waarden hebben berekend, hoeven we ze alleen nog maar in onze beginvergelijking te stoppen en de raaklijn op te lossen:

$\tan {2π}/3={√3}/2}/{-1/2}$

$\tan {2π}/3=-√3$

What’s next?

Als je binnenkort deelneemt aan de SAT of ACT, moet je een beetje trigonometrie kennen zodat je het goed kunt doen op het wiskundegedeelte. Bekijk onze gidsen over trigonometrie op de SAT en ACT, zodat je precies weet wat je moet weten voor de testdag!

Naast het onthouden van de eenheidscirkel is het een goed idee om te leren hoe je getallen invoegt en hoe je antwoorden invoegt. Lees onze gidsen om alles te leren over deze twee handige strategieën, die je bij elke wiskundetoets kunt gebruiken – inclusief de SAT en ACT!

Heb je vrienden die ook hulp nodig hebben bij het maken van toetsen? Deel dit artikel!