Solving Real-World Problems

Een les voor de eerste en tweede klas

Een les voor brugklassers

door Chris Confer

Wanneer kinderen wiskunde gebruiken om problemen in de echte wereld op te lossen, leren ze dat wiskunde niet alleen iets is om voor de leraar te doen, maar dat het hun belangrijke instrumenten biedt om hun wereld vorm te geven. In deze les, die staat in Chris Confers nieuwe boek Teaching Number Sense, Grade 1 (Math Solutions Publications, 2005), wordt de kinderen gevraagd uit te zoeken hoeveel koekjes ze nodig hebben voor een traktatie voor de klas.

“Morgen is het Kinderdag,” zei ik, “en dat kunnen we vieren met koekjes. Ik wil best twee koekjes voor ieder van jullie meenemen, maar ik wil graag weten hoeveel koekjes. Wat moeten we weten om dit uit te zoeken?”

“Hoeveel koekjes?” vroeg Juanita.

“Ja, dat is wat we moeten weten-hoeveel koekjes we nodig hebben, zodat ieder van jullie er twee kan hebben. Hoeveel kinderen zitten er in onze klas?” ging ik verder. De kinderen waren het er over eens dat het er tweeëntwintig waren. Ik schreef Er zijn 22 kinderen op het bord. Toen voegde ik eraan toe Als elk kind 2 koekjes krijgt, hoeveel koekjes hebben we dan nodig?

“Je kunt tekeningen maken of blokjes gebruiken of iets anders om het uit te rekenen,” zei ik. “Je kunt alleen werken of met een partner of partners.”

Opnieuw vroeg ik: “Hoeveel kinderen zijn er in deze kamer?” De kinderen antwoordden: “Tweeëntwintig.”

“En hoeveel koekjes heeft ieder nodig?” “Twee koekjes,” zeiden ze.

“Ik wil dat ieder van jullie je antwoord en hoe je eraan bent gekomen op een stuk papier laat zien,” vervolgde ik. “Gebruik woorden, getallen en plaatjes om te laten zien wat je hebt gedaan.”

Alfredo begon stokfiguurtjes te tekenen en naast elk twee koekjes, maar na twee stokfiguurtjes liet hij dit idee varen. “Het is te moeilijk,” vertelde hij me. “Kan ik opnieuw beginnen?” Hij draaide zijn papier om en begon setjes van twee koekjes te tekenen. Elk paar koekjes had een iets grotere ruimte tussen het en het volgende paar.

Alejandrina, Navin, en Alicia hadden paren koekjes getekend en hadden de paren omcirkeld. Ze waren aan het tellen om te controleren of ze tweeëntwintig paren hadden. Navin had 2 1 2 1 2 1 2 … geschreven en telde met enen. “Vierenveertig!” zei hij triomfantelijk.

Lorena zette stippen voor haar koekjes. De paren koekjes waren duidelijk van elkaar gescheiden. Ze telde ze, tekende er nog een paar, en telde ze na van een tot hoeveel koekjes ze had.

Ik ging verder naar Sereslinda, die cirkels had gemaakt voor de koekjes, allemaal op een lijn, zonder enige ruimte tussen de paren koekjes. Ze stopte om de koekjes te tellen en kwam tot zestien. Ik vroeg me af wat ze nu zou doen.

Alfredo had besloten zijn paren koekjes te omcirkelen. “Deze horen bij elkaar,” zei hij. “Het zijn twee kinderen.” Het leek erop dat Alfredo begon te verwarren wat de cirkels voorstelden: waren het koekjes of kinderen? Ik besloot niet in te grijpen en te kijken of hij het zelf kon oplossen. (Zie figuur 1.)

Figuur 1. Hoewel hij paren had omcirkeld, toonde
Alfredo’s papier tweeëntwintig koekjes, in plaats van tweeëntwintig paren koekjes.

Sereslinda was ook begonnen paren koekjes te omcirkelen, misschien om te laten zien dat elk kind twee koekjes kreeg. Af en toe stopte ze om de paren koekjes te tellen. Toen ze er tweeëntwintig had, stopte ze.

Toen begon ze stokjesmensen te tekenen. Ze maakte er tien en begon toen getallen te schrijven om de andere kinderen in de klas te vertegenwoordigen. Haar getallen liepen op tot tweeëntwintig, maar ze had maar elf stokjesfiguren en tien getallen getekend. Sereslinda had zich vergist in de telling, maar ik was geïnteresseerd in hoe ze was overgestapt op een efficiëntere manier van representeren: met getallen in plaats van tekeningen.

Ik keek toe hoe Sereslinda begon te controleren of ze genoeg paren koekjes had voor elk kind in de klas. Ze trok lijnen om elke stokpersoon met een koekjespaar te verbinden of elk cijfer met een koekjespaar. Maar dit werd een onhandige representatiestrategie. (Zie figuur 2.) Sereslinda begon gefrustreerd te raken. Het was tijd om in te grijpen.

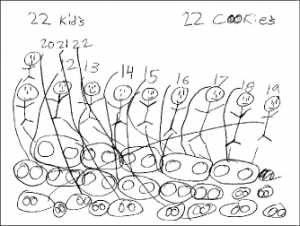
Figuur 2. Sereslinda heeft lijnen getrokken om haar stok
figuren te verbinden met paren koekjes. De vele lijnen op
de tekening brachten haar in verwarring, en ze veranderde haar
antwoord van vierenveertig in tweeëntwintig.

“Weet je wat voor slims ik je zie doen?” Vroeg ik aan Sereslinda. “Je past het aan om te controleren of je voor elke persoon twee koekjes hebt door lijnen te trekken. Dat werkt geweldig voor kleinere getallen, maar het wordt moeilijk met grotere getallen zoals tweeëntwintig. Mag ik je een suggestie doen?” Ze knikte. “Je kunt proberen elk paar van twee koekjes aan te wijzen en te kijken of je tweeëntwintig paren telt, net zoals we tweeëntwintig kinderen hebben.” Ik demonstreerde dit voor haar en ze ging zelf verder met tellen.

“Het is genoeg,” zei ze tegen me. Ik was blij dat deze alternatieve strategie nuttig voor haar was gebleken.

Lorena had tweeëntwintig paar koekjes gemaakt en begon ze in het Engels vanaf één te tellen. Ze vergiste zich halverwege en herkende op een of andere manier haar fout. “Misschien wil je in het Spaans tellen,” stelde ik voor. Als kinderen iets moeilijks doen, hebben ze vaak meer succes als ze hun eerste taal gebruiken.

Lorena begon opnieuw te tellen in het Spaans, en telde verder vanaf twee. Ze deed dit verschillende keren, ervoor zorgend dat ze juist telde. Lorena schreef zorgvuldig 44 koekjes bovenaan haar blad. (Zie figuur 3.)

Figuur 3. Lorena tekende tweeëntwintig paren van koekjes en telde daarna met enen, in het Spaans, tot vierenveertig.

Ik keerde terug naar Sereslinda. Op haar papier stonden tweeëntwintig paar koekjes. “Hoeveel koekjes moeten we hebben?” Vroeg ik. Sereslinda telde de groepjes van twee. “We hebben tweeëntwintig koekjes nodig,” kondigde ze aan.

“Dus we hebben tweeëntwintig kinderen, en elk kind krijgt twee koekjes, en we moeten tweeëntwintig koekjes meenemen?” vroeg ik. Sereslinda knikte en schreef 22 koekjes boven aan haar papier.

“Ze heeft gelijk,” zei Alfredo. Maar zijn papier had een heel andere voorstelling: slechts tweeëntwintig koekjes in plaats van tweeëntwintig paar koekjes.

Het voorstellen van twee koekjes voor elk kind is moeilijk, omdat er een hoeveelheid kinderen is die relevant is en een hoeveelheid koekjes die niet overeenkomt met het eerste getal, maar een verdubbeling van dat getal voorstelt. Na het voorstellen van deze verschillende hoeveelheden, moeten de kinderen onthouden en interpreteren welke welke is.

Na een tijdje verzamelde ik de kinderen op het tapijt en vroeg: “Hoeveel koekjes moet ik meebrengen als jullie met tweeëntwintig zijn en elk twee koekjes nodig heeft?” Ik vroeg Alfredo om eerst te delen.

“Er zijn twee kinderen hier,” zei Alfredo, wijzend naar de twee gestippelde cirkels die hij had getekend om koekjes voor te stellen. “En twee kinderen hier en twee kinderen hier. En dat maakt één, twee, drie, vier, vijf, zes, zeven, acht, negen, tien, elf, twaalf, dertien, veertien, vijftien, zestien, zeventien, achttien, negentien, twintig, eenentwintig, tweeëntwintig. En er zijn tweeëntwintig kinderen en tweeëntwintig koekjes.”

“Dus jij denkt dat als we tweeëntwintig koekjes hebben, er genoeg zal zijn voor ieder van jullie om twee koekjes te hebben,” zei ik. Alfredo knikte.

“Hoeveel van jullie zijn het ermee eens dat we tweeëntwintig koekjes nodig hebben?” vroeg ik. Ongeveer een derde van de kinderen stak zijn hand op. Ik schreef 22 koekjes op het bord.

Ik vroeg Lorena als volgende om te delen.

“We moeten alle tweeëntwintig kinderen zien en de koekjes tellen,” zei Lorena, wijzend op de paren koekjes die ze had getekend. “Het is een, twee, drie, vier…” Ze telde tot vierenveertig en zag dat elk paar uit twee koekjes bestond.

“Nee,” zei Alfredo. “Het zijn er tweeëntwintig.”

“Laten we eens kijken wat Lorena heeft getekend. Waar zijn de kinderen?” Vroeg ik haar. Ze wees naar elk paar koekjes en zei: “Dit is voor mij en dit is voor Sereslinda en dit is voor Heriberto . . . “

“Je liet een spatie tussen elk koekje om te laten zien dat het volgende paar koekjes voor een andere persoon was. En toen heb je alle koekjes geteld?” Vroeg ik. Lorena knikte. We telden alle koekjes die Lorena had getekend en kwamen tot vierenveertig. Ik schreef 44 koekjes op het bord.

“Dus we zijn het niet eens,” zei ik tegen de groep. “Sommigen van jullie denken dat we tweeëntwintig koekjes nodig hebben en sommigen denken dat het vierenveertig is. Hoe kunnen we dat zeker weten?”

“Geef ons de koekjes,” riepen sommige kinderen.

“Maar ik heb geen koekjes,” zei ik. “Ik moet weten hoeveel ik er mee moet nemen.” “We kunnen net alsof koekjes gebruiken,” zei Carina.

“Wat kunnen we gebruiken?” Vroeg ik. “Blokjes,” stelde Heriberto voor.

We gaven een zak met blokjes rond in de kring, en ik zorgde ervoor dat de kinderen er regelmatig aan werden herinnerd wat de blokjes voorstelden. “Twee koekjes voor Cristina, twee koekjes voor Heriberto. . .

We zetten alle kubussen op een rij, waarbij we de kubusparen bij elkaar hielden. Toen telden we de kubussen vanaf één. We eindigden met vierenveertig. “Dus we hebben tweeëntwintig kinderen en vierenveertig koekjes,” zei ik. Ik schreef 44 koekjes op het bord.

“Breng er vierenveertig mee,” zei Carina.

De volgende dag bracht ik vierenveertig koekjes mee en de kinderen waren dolblij dat ze er elk twee kregen.