Volume berekenen
Op deze pagina wordt uitgelegd hoe je het volume van vaste voorwerpen berekent, dat wil zeggen hoeveel er in een voorwerp past als je het bijvoorbeeld zou vullen met een vloeistof.
Area is de maat voor hoeveel ruimte er in een tweedimensionaal voorwerp zit (zie onze pagina: Oppervlakte berekenen voor meer).
Volume is de maat voor hoeveel ruimte er in een driedimensionaal voorwerp zit. Onze pagina over driedimensionale vormen legt de basis van zulke vormen uit.
In de echte wereld is het berekenen van volume waarschijnlijk niet iets dat je zo vaak zult gebruiken als het berekenen van oppervlakte.
Hoewel het nog steeds belangrijk kan zijn. Als je het volume kunt berekenen, kun je bijvoorbeeld uitrekenen hoeveel verpakkingsruimte je hebt bij een verhuizing, hoeveel kantoorruimte je nodig hebt, of hoeveel jam er in een pot past.
Het kan ook nuttig zijn om te begrijpen wat de media bedoelen als ze het hebben over de capaciteit van een dam of het debiet van een rivier.
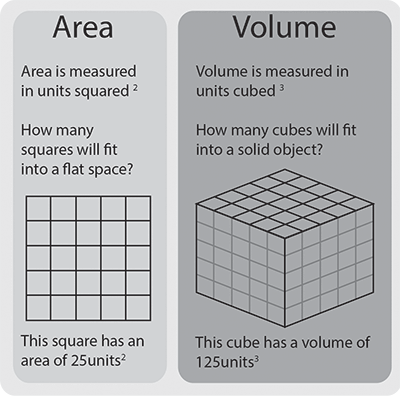
Eenheden
Area wordt uitgedrukt in vierkante eenheden, omdat het twee metingen zijn die met elkaar worden vermenigvuldigd.
Volume wordt uitgedrukt in kubieke eenheden, omdat het de som is van drie metingen (lengte, breedte en diepte) die met elkaar worden vermenigvuldigd. Kubieke eenheden zijn cm3, m3 en cubic feet.
WAARSCHUWING!
Volume kan ook worden uitgedrukt als vloeistofinhoud.
Metrisch stelsel
In het metrisch stelsel wordt vloeistofinhoud gemeten in liters, wat direct vergelijkbaar is met de kubieke maat, want 1ml = 1cm3. 1 liter = 1.000 ml = 1.000cm3.
Imperial/Engels systeem
In het imperiale/Engelse systeem zijn de equivalente metingen fluid ounces, pints, quarts en gallons, die niet gemakkelijk te vertalen zijn naar kubieke voet. Het is daarom het beste om het bij vloeibare of vaste volume-eenheden te houden.
Voor meer, zie onze pagina over maatstelsels
Basisformules voor het berekenen van volume
Volume van rechthoekige vaste stoffen

Waar de basisformule voor de oppervlakte van een rechthoekige vorm lengte × breedte is, is de basisformule voor het volume lengte × breedte × hoogte.
Hoe je naar de verschillende dimensies verwijst, verandert niets aan de berekening: je kunt bijvoorbeeld ‘diepte’ gebruiken in plaats van ‘hoogte’. Waar het om gaat is dat de drie dimensies met elkaar worden vermenigvuldigd. Je kunt vermenigvuldigen in welke volgorde je maar wilt, het antwoord verandert er niet door (zie onze pagina over vermenigvuldigen voor meer informatie).
Een doos met de afmetingen 15 cm breed, 25 cm lang en 5 cm hoog heeft een volume van:
15 × 25 × 5 = 1875cm3
Volume van prisma’s en cilinders
Deze basisformule kan worden uitgebreid om ook het volume van cilinders en prisma’s te berekenen. In plaats van een rechthoekig uiteinde heb je gewoon een andere vorm: een cirkel voor cilinders, een driehoek, zeshoek of, inderdaad, elke andere veelhoek voor een prisma.
In feite is voor cilinders en prisma’s het volume de oppervlakte van een zijde vermenigvuldigd met de diepte of hoogte van de vorm.
De basisformule voor volume van prisma’s en cilinders is dus:
Area van de eindvorm × de hoogte/diepte van het prisma/cilinder.
Volume van kegels en piramiden
Hetzelfde principe als hierboven (breedte × lengte × hoogte) geldt voor het berekenen van het volume van een kegel of een piramide, behalve dat, omdat ze in een punt uitkomen, het volume slechts een deel is van het totaal dat het zou zijn als ze in dezelfde vorm rechtdoor zouden gaan.
Het volume van een kegel of piramide is precies een derde van wat het zou zijn voor een doos of cilinder met hetzelfde grondvlak.
De formule is dus:
Bereik van het grondvlak of de eindvorm × de hoogte van de kegel/piramide × 1/3
Rug naar onze pagina Oppervlakte berekenen als je niet meer weet hoe je de oppervlakte van een cirkel of driehoek moet berekenen.
Om bijvoorbeeld het volume van een kegel met een straal van 5 cm en een hoogte van 10 cm te berekenen:
De oppervlakte binnen een cirkel = πr2 (waarbij π (pi) ongeveer 3,14 is en r de straal van de cirkel is).
In dit voorbeeld is oppervlakte van basis (cirkel) = πr2 = 3,14 × 5 × 5 = 78,5cm2.
78,5 × 10 = 785
785 × 1/3 = 261,6667cm3

Volume van een bol
Zoals bij een cirkel heb je π (pi) nodig om het volume van een bol te berekenen.
De formule is 4/3 × π × straal3.
Je vraagt je misschien af hoe je de straal van een bol zou kunnen uitrekenen. Behalve een breinaald erdoor steken (effectief, maar terminaal voor de bal!), is er een eenvoudiger manier.
Je kunt de afstand rond het breedste punt van de bol direct meten, bijvoorbeeld met een meetlint. Deze cirkel is de omtrek en heeft dezelfde straal als de bol zelf.
De omtrek van een cirkel bereken je als 2 x π x straal.
Om de straal te berekenen uit de omtrek ga je:
Deel de omtrek door (2 x π).
Werkvoorbeelden: Volume berekenen
Voorbeeld 1

Bereken het volume van een cilinder met een lengte van 20cm, en waarvan het ronde uiteinde een straal heeft van 2,5cm.
Bereken eerst de oppervlakte van een van de ronde uiteinden van de cilinder.
De oppervlakte van een cirkel is πr2 (π × straal × radius). π (pi) is ongeveer 3,14.
De oppervlakte van een uiteinde is dus:
3,14 x 2,5 x 2,5 = 19,63cm2
Het volume is de oppervlakte van een uiteinde vermenigvuldigd met de lengte, en is dus:
19.63cm2 x 20cm = 392,70cm3

Voorbeeld 2
Welke bol is groter in volume, een bol met straal 2cm of een piramide met basis vierkant 2,5cm en hoogte 10cm?
Bereken eerst het volume van de bol.
Het volume van een bol is 4/3 × π × straal3.
Het volume van de bol is dus:
4 ÷ 3 x 3,14 × 2 × 2 = 33,51cm3
Bereken vervolgens het volume van de piramide.
Het volume van een piramide is 1/3 × oppervlakte van het grondvlak × hoogte.
Afmeting grondvlak = lengte × breedte = 2,5cm × 2,5cm = 6,25cm2
Hoeveelheid is dus 1/3 x 6,25 × 10 = 20,83cm3
De bol is dus groter in volume dan de piramide.
Bereken het volume van onregelmatige vaste stoffen
Net zoals je de oppervlakte van onregelmatige tweedimensionale vormen kunt berekenen door ze op te splitsen in regelmatige vormen, kun je hetzelfde doen om het volume van onregelmatige vaste stoffen te berekenen. Splits de vaste stof op in kleinere delen tot je alleen vaste stoffen hebt waar je gemakkelijk mee kunt werken.
Werkvoorbeeld
Bereken het volume van een watercilinder met een totale hoogte van 1m, een diameter van 40cm, en waarvan het bovenste gedeelte half bolvormig is.

Je verdeelt de vorm eerst in twee delen, een cilinder en een halve bol (een halve bol).
Het volume van een bol is 4/3 × π × radius3. In dit voorbeeld is de straal 20cm (de helft van de diameter). Omdat de top halfbolvormig is, zal het volume de helft zijn van dat van een volle bol. Het volume van dit deel van de vorm is dus:
0,5 × 4/3 × π × 203 = 16.755,16cm3
Het volume van een cilinder is oppervlakte van het grondvlak × hoogte. Hier is de hoogte van de cilinder de totale hoogte min de straal van de bol, die is 1m – 20cm = 80cm. De oppervlakte van het grondvlak is πr2.
Het volume van het cilindrische gedeelte van deze vorm is dus:
80 × π × 20 × 20 = 100.530,96cm3
Het totale volume van deze watercontainer is dus:
100.530,96 + 16.755,16 = 117.286,12cm3.
Dit is een vrij groot getal, zodat je het misschien liever omrekent naar 117,19 liter door te delen door 1.000 (want er zitten 1000cm3 in een liter). Het is echter volkomen juist om het uit te drukken in cm3, omdat het probleem niet vraagt om het antwoord in een bepaalde vorm uit te drukken.
In Conclusie…
Met behulp van deze principes moet je nu, indien nodig, in staat zijn om het volume van bijna alles in je leven te berekenen, of dat nu een verpakkingskrat, een kamer of een waterfles is.