Wat is het verschil tussen PNP en NPN?

Dit artikel verscheen in Microwaves & RF en is hier met toestemming gepubliceerd.

Wat u leert:

• De maximale doorvoer van een kanaal als functie van de symbol rate en bandbreedte.
• De maximale verwerkingscapaciteit van een kanaal als functie van ruisinterferentie.
• Hoe verwerkingsoverwegingen helemaal teruggaan naar de gebruiker.

Het is heel gemakkelijk en normaal om je te concentreren op de hoofdkenmerken van de hoofdcomponenten van een communicatiesysteem of -verbinding, en andere zaken en kwesties als bijkomstig en niet zo belangrijk te beschouwen. Dat dit verrassend vaak is gebeurd met satellietcommunicatieverbindingen, vooral mobiele verbindingen op afstand, is de reden voor deze missive.

Hier volgt een hypothetische situatie. Je bent een soldaat. U wordt ingezet in een bergachtig gebied in het Midden-Oosten, draagt een oudere Intelsat satellietterminal voor onmiddellijke toegang tot het hoofdkwartier, en het hoofdkwartier heeft een 72-MHz transponder geleased voor uw exclusief gebruik.

Een mooie, veilige plek is een grot, dus je sluit een communicatiekabel aan op de satellietterminal bij de ingang van de grot en gaat achterover zitten om in te checken met je werkstation dat met een quadrature phase-shift keying (QPSK) modem is verbonden met de terminal. Inchecken gaat prima, maar de communicatie is belabberd. Het satellietbedrijf garandeert je 72 Mb/s (1 bit per Hz), maar je krijgt nauwelijks minder dan 35 Mb/s. Had je een nieuwere terminal moeten nemen? Had je een ander systeem moeten gebruiken?

Nyquist Maximum Data Rates

Het eigenlijke antwoord is wat Harry Nyquist en Claude Shannon zeiden over maximale datasnelheden over elk kanaal, inclusief die communicatiekabel. Harry Nyquist merkte op, zoals grondig is gedocumenteerd1, dat het maximale aantal bits dat je door een kanaal kunt krijgen (ruis buiten beschouwing gelaten) is:

Max R = 2 H Log2V

waarbij H de kanaalbandbreedte is en V het aantal discrete symbolen (binary phase-shift keying, of BPSK, is 2, QPSK is 4, enzovoort).

Als u niet bekend bent met log2, is het niet moeilijk als u er eenmaal aan gewend bent. De log2V is eenvoudigweg de exponent waartoe 2 moet worden verheven om gelijk te zijn aan V. Dus, als V BPSK (2) is, dan is de uitdrukking log2V eenvoudigweg 1, omdat 21 eigenlijk 2 is; en als V QPSK (4) is, dan is de uitdrukking log2V 2, omdat 22 eigenlijk 4 is, enzovoort.

Als u een 10-MHz Cat 3 kabel gebruikt, dan is de maximale datasnelheid IN de satellietterminal BPSK 20 Mb/s, QPSK 40 Mb/s, en 8PSK 30 Mb/s, als een functie van de log2 relaties. Figuur 1 toont het aantal toestanden en hun log naar het basis 2 equivalent. Daarom is de Nyquist-limiet, bij gebruik van de QPSK-modem, 40 Mb/s.

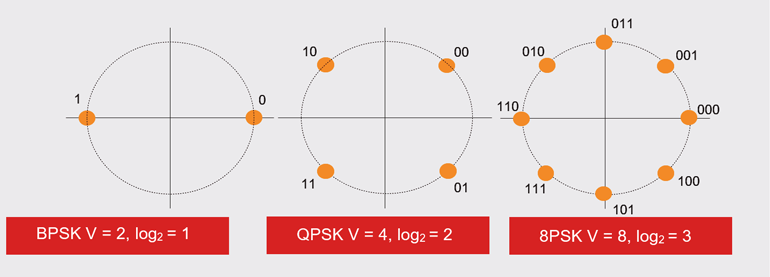1. BPSK, met twee toestanden, heeft een log2-waarde van 1; QPSK, met vier toestanden, heeft een log2-waarde van 2; enzovoort.

Shannon Maximale Gegevenssnelheden

Wel, Harry Nyquist werkte aan de kwestie van maximale gegevenssnelheden zonder rekening te houden met ruis, terwijl Claude Shannon dit strikt als een functie van ruis deed. Zijn vergelijking2 luidt:

Max R = H log2 (1 + SNR)

waarbij H weer de bandbreedte van het kanaal is en de SNR het signaalvermogen gedeeld door het ruisvermogen is, meestal gegeven in dB. Laten we aannemen dat de SNR op diezelfde Cat 3 kabel ongeveer 30 dB of 1.000 in ruwe getallen is (de SNR moet worden omgezet in zijn rationele waarde om een exponentiële berekening te maken). Aangezien we de schaal van de exponentialen van 2 hebben opgevoerd, kunnen we dat gewoon blijven doen. Figuur 2 toont die progressie.

2. Een getal, weergegeven op de bovenste regel, heeft een exponentiële waarde, weergegeven op de onderste regel, en toont de betekenis aan van de ruistemperatuur van het systeem in relatie tot de kanaaldoorvoer.

Als we omwille van de eenvoud een beetje afronden, ligt 1.001 dichter bij 1.024 dan elke andere toename en 2 verheven tot de 10e macht geeft je een waarde die veel dichter ligt dan elke andere exponent. Zittend in je grot met een 10-MHz bandbreedte Cat 3 kabel, zegt Claude Shannon dat je een datasnelheid van 10 x 106 (10) = 100 Mb/s zou moeten krijgen.

Als Claude Shannon zegt dat je een maximale datasnelheid van 100 Mb/s in de satelliet communicatie terminal kunt krijgen en Harry Nyquist zegt dat je slechts 40 Mb/s van en naar je met QPSK uitgeruste werkstation kunt krijgen, wie heeft er dan gelijk?

Laten we eens naar een andere analogie kijken. De Universiteit van Notre Dame heeft een academisch beperkt maar relatief goed football team. Aan de andere kant heeft het een geweldige fanfare, omdat uitmuntende musici vaak uitmuntende middelbare scholieren zijn. Om op het veld te komen, moet de band door twee bogen marcheren, één waar 15 leden naast elkaar mogen staan en één waar 10 leden naast elkaar mogen staan. Hoe groot is het aantal leden per rij? Nyquist en Shannon zijn geen concurrenten. Het zijn gewoon twee verschillende poorten met twee verschillende beperkingen.

Het is niet alleen het grote systeem. Het zijn de ‘go-intas’ en de ‘go-outas’, helemaal tot aan de handen die op het toetsenbord typen. En de oorspronkelijke verhandelingen, gepubliceerd door de natuurkundige Nyquist3 en de wiskundige/ingenieur Shannon4 hebben ons nog steeds iets te zeggen.

1. Een voorbeeld van de vergelijking is te vinden in een willekeurige uitgave van Data and Computer Communications door William Stallings, vermeld onder Nyquist Bandwidth. Opmerking: verschillende auteurs gebruiken verschillende letters om datasnelheid, bandbreedte, enz. aan te duiden.

2. Net als Nyquist is de vergelijking te vinden in elke editie van Data and Computer Communications door William Stallings, deze staat vermeld onder Shannon Capacity Formula. Opmerking: Verschillende auteurs gebruiken verschillende letters om datasnelheid, bandbreedte, enz. aan te duiden.

3. Bepaalde onderwerpen in de telegraaf transmissietheorie (die de limiet impliceerden) werden gepresenteerd op de Winter Conventie van de AIEE, New York, N.Y., 13-17 februari, 1928. Het werd opnieuw gepubliceerd als een “Classic Paper” in de Proceedings van het IEEE in februari 2002.

4. “Communications in the Presence of Noise” werd gepubliceerd in de Proceedings van het IRE in januari 1949, negen jaar nadat het was geschreven.