Oval

Ein Oval ist eine Kurve, die einem gequetschten Kreis ähnelt, aber, anders als die Ellipse, ohne genaue mathematische Definition. Das Wort Oval leitet sich von dem lateinischen Wort „ovus“ für Ei ab. Im Gegensatz zu Ellipsen haben Ovale manchmal nur eine einzige Spiegelsymmetrieachse (statt zwei).

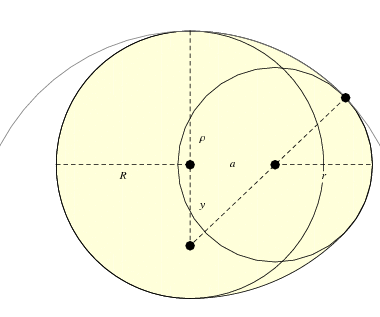
Die oben dargestellte Variante kann mit einem Zirkel konstruiert werden, indem Bögen mit unterschiedlichen Radien so miteinander verbunden werden, dass die Mittelpunkte der Bögen auf einer Linie liegen, die durch den Verbindungspunkt geht (Dixon 1991). Albrecht Dürer benutzte diese Methode, um eine römische Buchstabenschrift zu entwerfen. Wenn der Abstand zwischen linkem und rechtem Großbuchstaben ist und die Radien und sind, jeweils mit und , dann ist der Mittelpunkt und Radius des Verbindungskreises sind

			(1)
			(2)

Nennen Sie die drei Kreise , und . Der obere Schnittpunkt von und sei , der Winkel zwischen der senkrechten gestrichelten Linie und der Linie durch sei , und der Winkel zwischen dem horizontalen Radius von und der gestrichelten Linie durch sei . Dann

			(3)
			(4)
			(5)
			(6)

und die Hälfte der vom Oval eingeschlossenen Fläche ist die Summe der Flächen des linken Viertelkreises, dem Sektor von und dem Sektor von abzüglich der Fläche des dreieckigen Teils des Sektors von , der unterhalb der -Achse liegt, also

			(7)
			(8)
			(9)

Wie erwartet, reduziert sich diese Formel auf den Flächeninhalt eines Kreises

(10)

für , und zur Fläche eines Stadions

(11)

für .