12.4: Techniki konwersji cyfrowo-analogowej
Podstawowy konwerter cyfrowo-analogowy to niewiele więcej niż ważony wzmacniacz sumujący. Każdy kolejny bit w słowie cyfrowym reprezentuje poziom, który jest dwa razy większy od poprzedniego bitu. Jeśli każdy bit jest traktowany jako dany prąd lub napięcie, rosnące poziomy mogą być wytwarzane przez zastosowanie różnych wzmocnień na wejściach sumujących. Prosty konwerter czterobitowy pokazany jest na rysunku
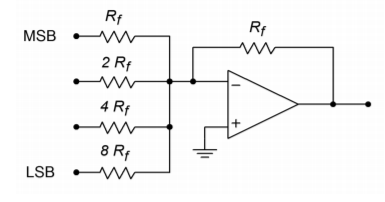
Rysunek
Rysunek
: Prosty konwerter 4-bitowy.
Ten układ może reprezentować ^2^4, czyli 16, różnych poziomów. Każde wejście jest sterowane przez prosty wysoki/niski poziom logiczny, który reprezentuje 1 lub 0 dla danego bitu. Należy zauważyć, że rezystory wejściowe różnią się o współczynnik 2. Wzmocnienie dla górnej ścieżki wynosi \(R_f/R_f\), czyli jedność. Wejście to jest używane dla najbardziej znaczącego bitu słowa wejściowego (MSB). Kolejne wejście wykazuje wzmocnienie równe \(R_f / (2R_f)\), czyli 0,5. Trzecie wejście wykazuje wzmocnienie 0,25, a ostatnie wejście wykazuje wzmocnienie 0,125. Wejście końcowe ma najniższe wzmocnienie i jest używane dla najmniej znaczącego bitu słowa wejściowego (LSB). Jeśli słowo wejściowe miałoby większą rozdzielczość (tj. więcej bitów), dodane zostałyby dodatkowe kanały, z których każdy miałby połowę wzmocnienia poprzedniego wejścia. Aby lepiej zrozumieć proces konwersji, przyjrzyjmy się kilku reprezentatywnym wejściom i wyjściom.
Obwód z rysunku może być wysterowany przez proste obwody logiczne 5 V typu TTL. Napięcie 5 V oznacza logiczny stan wysoki, podczas gdy 0 V oznacza logiczny stan niski. Jaki jest poziom wyjściowy, jeśli słowo wejściowe ma wartość 0100? Ponieważ logiczny stan wysoki reprezentuje 5 V, 5 V jest przykładane do drugiego wejścia. Wszystkie pozostałe wejścia otrzymują logiczny stan niski, czyli 0 V. Wyjście jest sumą sygnałów wejściowych (pamiętaj, że jest to odwracające się lato, więc końcowe wyjście powinno mieć odwrócony znak).
Więc wartość 4 (binarne 100) odpowiada potencjałowi 2,5 V. Jeśli zwiększymy wartość słowa do 9 (binarne 1001), zobaczymy
Minimalna wartość wyjściowa występuje przy binarnym 0000, (0 V), a maksymalna przy binarnym 1111 (-9,375 V). Wielkość kroku jest równa poziomowi logicznemu pomnożonemu przez minimalne wzmocnienie; w tym przypadku jest to 0,625 V. Zauważ, że wartość wyjściowa może być znaleziona po prostu przez pomnożenie wartości słowa wejściowego przez minimalną wielkość kroku. Należy również zauważyć, że sygnał wyjściowy jest unipolarny (w tym przykładzie zawsze ujemny).
Odwzorowanie cyfrowe składa się oczywiście z sekwencji słów, a nie tylko z jednego słowa. W rzeczywistości obwody logiczne stale podają wzmacniaczowi sumującemu nowe słowa w określonym z góry tempie. Ze względu na zmieniające się wejścia, wyjście konwertera również ulega ciągłym zmianom. Używając naszych wcześniej obliczonych wartości, jeśli konwerter jest zasilany sekwencją \(0000, 0100, 1001, 1111, \) wyjście będzie się zmieniać od 0 V do -2,5 V, do -5.625 V, aż do końcowej wartości -9,375 V. Wyjście to jest przedstawione na rysunku \(\PageIndex{2}).
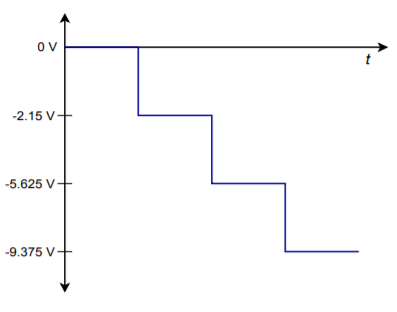
Rysunek \(\PageIndex{2}): Wyjście z czterema słowami cyfrowymi.
Jeśli ta sekwencja jest powtarzana w kółko, powstaje przebieg przedstawiony na rysunku \(\PageIndex{3}}). Zauważ, że powstaje fala typu „stair-step”. Można też pomyśleć o tym jako o bardzo zgrubnej formie funkcji rampy. Lepsza rampa powstałaby, gdybyśmy użyli wszystkich dostępnych wartości dla sekwencji wejściowej, tak jak w przypadku 0000, 0001, 0010, 0011, 1111). Aby usunąć ujemne przesunięcie DC i uczynić sygnał bipolarnym, wystarczy przepuścić go przez kondensator sprzęgający. Częstotliwość tego przebiegu jest kontrolowana przez szybkość, z jaką słowa są podawane do konwertera. Zauważ, że zwiększając rozdzielczość i liczbę słów podawanych do konwertera w cyklu, można uzyskać bardzo bliskie przybliżenie do idealnej funkcji rampy. Zmieniając słowa wejściowe na inne sekwencje, możemy uzyskać bardzo różnorodne kształty fal wyjściowych. Na tym właśnie polega koncepcja cyfrowego generatora funkcji arbitralnych. Generator funkcji arbitralnych umożliwia tworzenie kształtów fal wykraczających poza proste sinusoidy/kwadraty/trójkąty, które można znaleźć w typowych laboratoryjnych generatorach funkcji. Przyjrzymy się bliżej temu konkretnemu elementowi wyposażenia testowego nieco później.
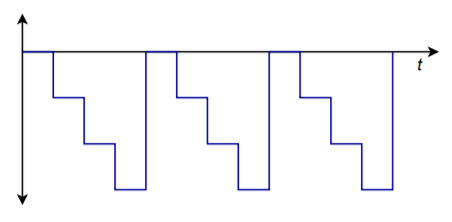
Rysunek ™: Wyjście cykliczne.
W celu zwiększenia rozdzielczości wydaje się, że wszystko, co trzeba zrobić ze wzmacniaczem sumującym, to dodać dodatkowe kanały z coraz większymi rezystorami. Niestety, rozmiary rezystorów szybko stają się niepraktyczne i konieczne jest inne podejście. Na przykład, system 16-bitowy wymagałby, aby rezystor LSB był równy 65,536 \(R_f\). Jednym z problemów jest to, że wynikający z tego mały prąd wejściowy może zostać przyćmiony przez prądy biasu i offsetu. Ponadto, wysoka dokładność komponentów jest potrzebna dla bardziej znaczących wejść pod względem rezystorów wejściowych i sygnałów sterujących. Zbyt duże rezystory mogą również przyczyniać się do powstawania dodatkowych szumów. Standardowe rozwiązanie tego problemu polega na zastosowaniu sieci dzielnika rezystancyjnego \(R/2R\).
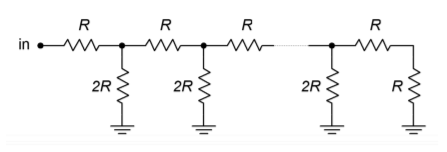
Rysunek \(\PageIndex{4}): \Sieć drabinkowa R/2R
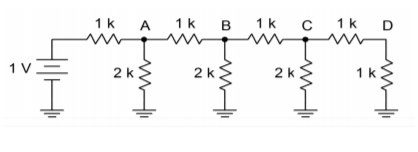
Rysunek \(\PageIndex{5}): 4-stopniowa drabina.
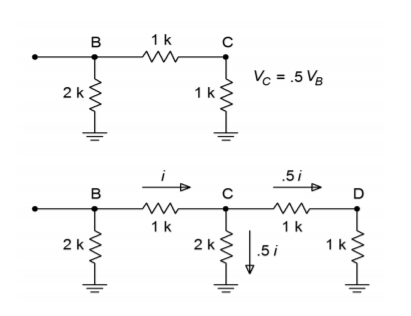
Rysunek ™(®PageIndex{6}}): Analiza drabinkowa. a. Obwód równoważny (góra). b. Podział prądu (dół).
Jeśli spojrzysz na sekcję obwodu równoważnego z rysunku \(\PageIndex{6}), zauważysz, że ta część wygląda teraz dokładnie tak samo jak końcowa część oryginalnej sieci. Oznacza to, że za każdym razem, gdy sekcja jest upraszczana i analizowana, wynikiem będzie zmniejszenie o połowę napięcia i prądu. Jest już oczywiste, że napięcie w punkcie D musi być o połowę mniejsze od napięcia w punkcie C, które z kolei musi być o połowę mniejsze od napięcia w punkcie B. Jak można teraz udowodnić, wynika z tego, że napięcie na \B\ musi być równe połowie napięcia na \A. W podobny sposób, prąd płynący przez każdą nóżkę \u2R\u jest połową prądu płynącego poprzednio. (W przypadku podziału prądu, ostatni odcinek nie jest używany do wyprowadzenia prądu, ponieważ będzie on równy wartości z poprzedniego etapu). Zmniejszenie prądu o połowę jest właśnie tym, co jest potrzebne do binarnej reprezentacji cyfrowego słowa wejściowego.
Adaptacja sieci R/2R do przetwornika DA jest stosunkowo prosta. Sieć jest zasilana ze stabilnego źródła prądowego, a każdy element \(2R\) jest podawany do wzmacniacza sumującego. Szeregowo z każdym elementem Ω jest przełącznik półprzewodnikowy, który ustawia odpowiedni poziom logiczny. Jest to pokazane na rysunku (¢PageIndex{7}}), z siecią efektywnie położoną na boku. Gdy na danym bicie pojawi się logiczny stan wysoki, przełącznik zostaje zamknięty i prąd przepływa przez element 2R i trafia do wzmacniacza op. Zwróć uwagę, że prawy koniec rezystora jest w rzeczywistości na ziemi, ponieważ węzeł sumujący wzmacniacza op jest wirtualną masą. Jeśli pojawi się logiczny stan niski, przełącznik przekierowuje prąd do masy, omijając wzmacniacz operacyjny. W ten sposób, odpowiednio ważone prądy są sumowane i wykorzystywane do wytworzenia napięcia wyjściowego.
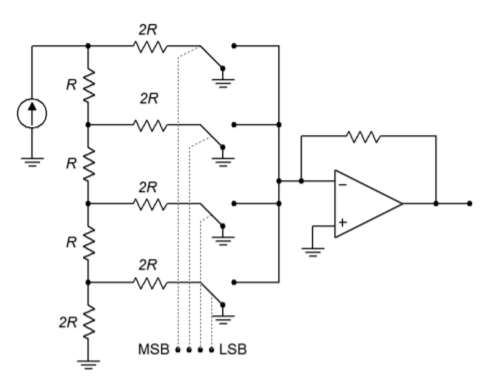
Rysunek \(\): Konwerter z drabinką R/2R.
Ta technika ma kilka zalet w porównaniu z prostszą wersją o wzmocnieniu ważonym. Po pierwsze, wszystkie gałęzie są zasilane z jednego wspólnego źródła prądowego. Dzięki temu nie ma potrzeby dopasowywania poziomu wyjściowego. Po drugie, wymagane są tylko dwie różne wartości rezystorów dla dowolnej liczby bitów, a nie niepraktycznie szeroki zakres, jak to miało miejsce wcześniej. Bardziej ekonomiczne jest kontrolowanie tolerancji tylko dwóch różnych części niż 12 lub 16. Zauważ, że małe prądy wejściowe są nadal generowane dla najmniej znaczących bitów, więc uwaga na bias wejściowy i prądy offsetowe pozostaje ważna.
12.4.1: Praktyczne ograniczenia przetwornika cyfrowo-analogowego
Prawdopodobnie najbardziej oczywistym ograniczeniem związanym z przetwornikiem DA jest jego szybkość. Wzmacniacz operacyjny używany w DAC musi być znacznie szybszy niż końcowe sygnały, które ma produkować. Dany przebieg wyjściowy może zawierać kilkadziesiąt pojedynczych punktów próbkowania w cyklu. Wzmacniacz op musi reagować na każdy punkt próbkowania. W związku z tym wymagane jest szerokie pasmo przenoszenia i duże szybkości narastania sygnału.
W arkuszach specyfikacji zintegrowanych przetworników C/A można znaleźć kilka ważnych parametrów, których warto być świadomym. Pierwszym z nich jest prędkość konwersji. Ta liczba mówi, ile czasu zajmuje przetwornikowi C/A przekształcenie cyfrowego słowa wejściowego w stabilne analogowe napięcie wyjściowe. Określa to maksymalną szybkość transmisji danych. Następnie dokładność i rozdzielczość. Rozdzielczość wskazuje liczbę dyskretnych kroków, które mogą być produkowane na wyjściu i jest określana przez liczbę dostępnych bitów. To nie jest to samo co dokładność. Dokładność składa się w rzeczywistości z kilku różnych czynników, w tym błędu przesunięcia, błędu i nieliniowości. Błąd przesunięcia jest zwykle mierzony przez zastosowanie całkowicie zerowego słowa wejściowego, a następnie pomiar sygnału wyjściowego. W idealnym przypadku sygnał ten będzie miał wartość zero woltów. Odchylenie od zera jest traktowane jako błąd przesunięcia. Skutkuje to tym, że wszystkie poziomy wyjściowe są niedokładne o stałe napięcie. Błąd offsetu jest stosunkowo łatwy do skompensowania w wielu aplikacjach poprzez zastosowanie równego offsetu o przeciwnej polaryzacji. Błąd wzmocnienia jest odchyleniem, które wpływa na każdy poziom wyjściowy o stałą wartość procentową. Jest to tak, jakby sygnał był przepuszczony przez mały wzmacniacz lub tłumik. Błąd ten może być skompensowany poprzez zastosowanie wzmacniacza o wzmocnieniu równym odwrotności błędu. Oba wzmocnienia skutecznie się zniosą. Efekt błędu offsetu i wzmocnienia pokazano na rysunkach \(\PageIndex{8}) i \(\PageIndex{9}).
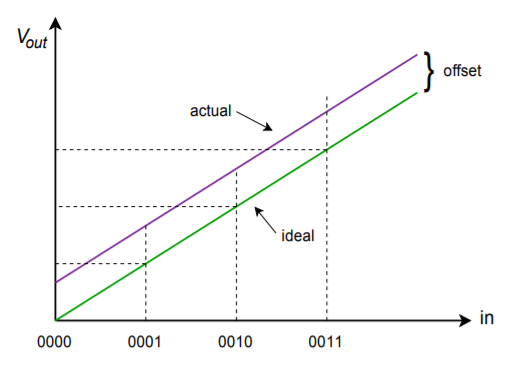
Rysunek \(\PageIndex{8}): Offset error only.
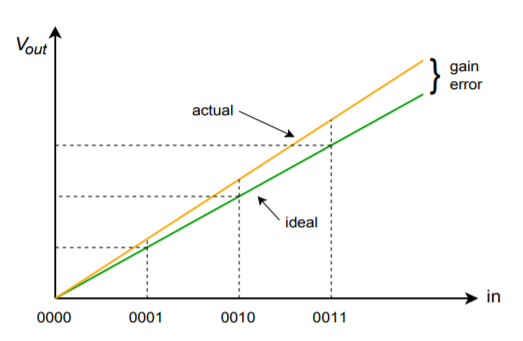
Figure \(\PageIndex{9}}): Tylko błąd wzmocnienia.
Błędy nieliniowości można podzielić na dwie formy: nieliniowość integralną i nieliniowość różnicową. Nieliniowość integralna wyszczególnia maksymalne przesunięcie między idealnymi wyjściami a rzeczywistymi wyjściami dla wszystkich możliwych wejść. Nieliniowość różnicowa wyszczególnia maksymalne odchylenie wyjścia w stosunku do jednej LSB spowodowane przez dwa sąsiadujące słowa wejściowe. Jeżeli nieliniowość różnicowa jest większa niż ≤ 1 LSB, system może być niemonotoniczny. Innymi słowy, wyższe cyfrowe słowo wejściowe może w rzeczywistości wytwarzać niższe analogowe napięcie wyjściowe. Te dwie formy błędu pokazane są na rysunku \(\PageIndex{10}). Należy zauważyć, że możliwe jest posiadanie wysokiej nieliniowości całkowej i jednocześnie umiarkowanej nieliniowości różnicowej. Taka sytuacja ma miejsce na rysunku \(\PageIndex{10b}}).
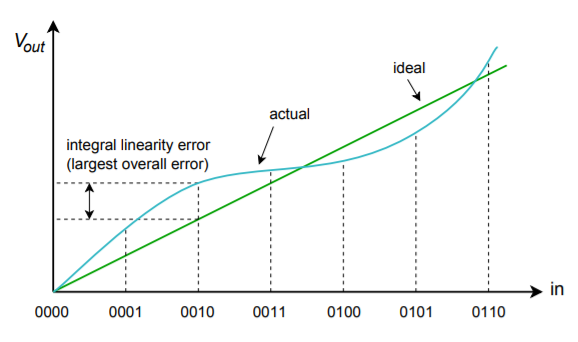
Rysunek \(\PageIndex{10a}}): Błąd liniowości Integralny błąd liniowości.
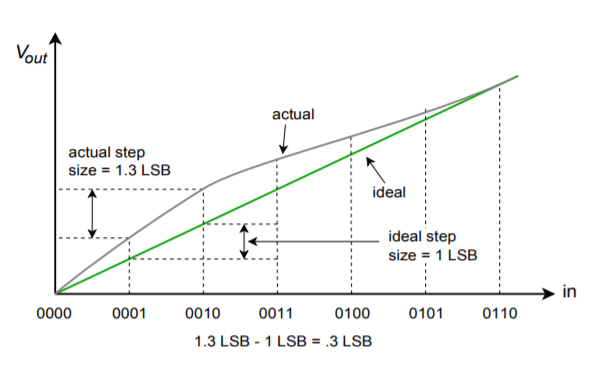
Rysunek \(\PageIndex{10b}): Błąd liniowości (ciąg dalszy) Różnicowy błąd liniowości (błąd względny przylegania).
Jak widać, dokładność zależy od dość złożonych czynników. Niektórzy producenci, chcąc sprowadzić to do jednej liczby, podają efektywną liczbę bitów w specyfikacji. Na przykład, 16-bitowy przetwornik C/A może być określony jako posiadający 14-bitową dokładność. Oznacza to, że 14 najbardziej znaczących bitów zachowuje się w sposób wyidealizowany, ale najniższe 2 bity mogą być tłumione przez błędy liniowości. Inną specyfikacją, którą czasami można zobaczyć, jest brak brakujących kodów. Oznacza to, że dla każdego wzrostu słowa wejściowego, będzie odpowiednia dodatnia zmiana poziomu wyjściowego.
W praktyce, standardowy konwerter DA jest używany z filtrem wyjściowym. Jak widać na poprzednich rysunkach, przebiegi produkowane przez DAC zawierają efekt uboczny w postaci schodków. Generalnie nie jest to zjawisko pożądane. Gwałtowne zmiany poziomu wyjściowego wskazują, że obecne są składowe o wyższych częstotliwościach. Wszystkie składowe powyżej częstotliwości Nyquista powinny być odfiltrowane za pomocą odpowiedniego filtra dolnoprzepustowego. Filtr ten nazywany jest czasem filtrem rekonstrukcyjnym lub wygładzającym. W niewłaściwie zaprojektowanym systemie filtr rekonstrukcyjny usunie niektóre składowe o najwyższej częstotliwości w paśmie (tj. składowe bezpośrednio poniżej częstotliwości Nyquista). Aby to skompensować, poziomy logiczne są często zatrzaskiwane do przetwornika C/A przez krótsze okresy, tworząc w ten sposób bardziej kolczasty wygląd, zamiast formy schodkowej. Efekt ten jest pokazany na rysunku \(\PageIndex{11}). Mimo, że ten kształt fali wydaje się mniej pożądany niż forma schodkowa, tworzy on wyższe poziomy dla najwyższych składowych, a po filtrowaniu, wynikiem jest gładsza ogólna odpowiedź częstotliwościowa.
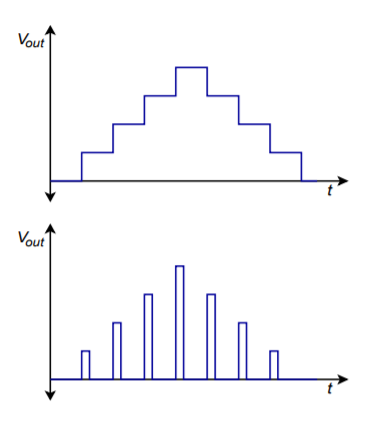
Rysunek \(\PageIndex{11}}): Rekonstrukcja wyjścia. a. Pełny okres zatrzasku (góra). b. Częściowy okres zatrzasku (dół).
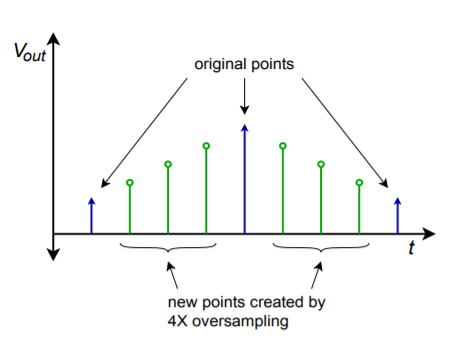
Aby jeszcze bardziej zwiększyć jakość kształtu fali wyjściowej, czasami stosuje się technikę znaną jako nadpróbkowanie. Podstawową ideą jest tworzenie nowych punktów próbkowania pomiędzy istniejącymi. Rezultatem jest znacznie większa gęstość danych, która, miejmy nadzieję, przyniesie dokładniejsze wyniki po filtrowaniu. Ponadto, wyższa częstotliwość danych może złagodzić wymagania stawiane filtrowi rekonstrukcyjnemu. Typowy system może używać czterokrotnego nadpróbkowania, co oznacza, że wyjściowa szybkość danych jest czterokrotnie większa od oryginalnej. Dlatego dla każdego słowa wejściowego należy dodać trzy nowe słowa. Efekt ten jest pokazany na rysunku
Rysunek
Rysunek
(\PageIndex{12}}): Nadpróbkowane dane wyjściowe.
Istnieje wiele sposobów na utworzenie nowych punktów próbkowania. Najbardziej oczywistym sposobem jest prosta interpolacja, ale nie daje ona najlepszych rezultatów. Inna technika polega na inicjalizacji nowych wartości na zero, a następnie przepuszczeniu strumienia danych przez cyfrowy filtr dolnoprzepustowy, który efektywnie oblicza właściwe wartości. Rozszerzeniem zasady nadpróbkowania jest technika delta-sigma. W delta-sigma, bardzo duże szybkości nadpróbkowania są używane w połączeniu z wyspecjalizowanymi algorytmami filtrów cyfrowych. Algorytmy te zasadniczo zamieniają wyższą prędkość danych na wolniejszą prędkość o zwiększonej rozdzielczości. Projektowanie i analiza systemów delta-sigma jest dość zaawansowana i wykracza poza zakres tego tekstu. Wystarczy powiedzieć, że techniki te mogą zwiększyć jakość sygnału wyjściowego i są szeroko stosowane w aplikacjach takich jak wysokiej jakości odtwarzacze audio CD i DVD.
12.4.2: Układy scalone przetworników cyfrowo-analogowych
Istnieje wiele możliwych zastosowań dla przetworników cyfrowo-analogowych, a szereg różnych układów scalonych rozwinęło się w celu zaspokojenia konkretnych potrzeb. Ogólnie rzecz biorąc, można je pogrupować w określone klasy, takie jak wysoka prędkość, wysoka rozdzielczość lub niski koszt. My przeanalizujemy trzy reprezentatywne typy. Urządzenia, którym się przyjrzymy to DAC0832; podstawowa jednostka 8-bitowa, DAC7545; jednostka 12-bitowa kompatybilna z mikroprocesorem oraz PCM1716; 24-bitowy przetwornik wysokiej jakości stosowany w przemyśle audio.
DAC0832
Ten układ scalony jest popularnym 8-bitowym przetwornikiem kompatybilnym z mikroprocesorem. DAC0830 i DAC0831 są podobne, ale o nieco mniejszej wydajności. Jest to przetwornik C/A z multiplikacją. Innymi słowy, sygnał wyjściowy jest funkcją cyfrowego słowa wejściowego i wejścia referencyjnego. W niektórych aplikacjach, wejście referencyjne nie jest stałe, ale raczej jest zmiennym sygnałem wejściowym. Lista funkcji i wyprowadzeń jest pokazana na rysunku \(\PageIndex{13}). Godne uwagi są: czas ustalania wynoszący tylko 1 s, niskie wymagania dotyczące zasilania i wysoka liniowość. Przetwornik DAC0832 może być używany zarówno w trybie samodzielnym, jak i z mikroprocesorem. Przebiegi przełączania pokazano na rysunku

Ryc: DAC0832. Reprinted courtesy of Texas Instrutment

Rysunek \(\PageIndex{14}): Przebiegi przełączania przetwornika DAC0832 Przedruk dzięki uprzejmości firmy Texas Instrutments
Ciekawe zastosowanie przetwornika DAC0832 można znaleźć na rysunku \(\PageIndex{15}). W zasadzie jest to sterowany cyfrowo filtr zmiennoprzecinkowy.
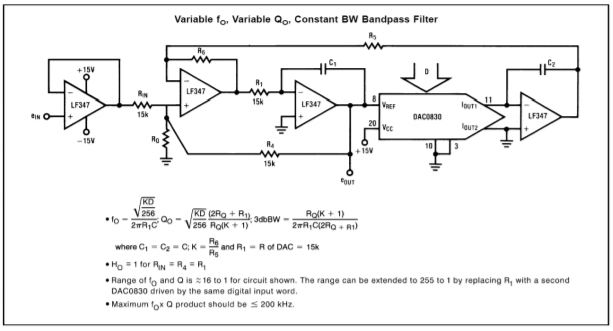
Rysunek \(\PageIndex{15}}): Aplikacja filtra zmiennoprzecinkowego DAC0832. Przedruk dzięki uprzejmości firmy Texas Instrutments
Zauważ, że konwerter zastępuje rezystor wejściowy drugiego integratora. Normalnie, rezystor ten byłby używany do konwersji napięcia wyjściowego pierwszego integratora na prąd wejściowy drugiego integratora. To zadanie jest teraz wykonywane przez DAC0832. Cyfrowe słowo wejściowe efektywnie ustawia konwersję napięcia na prąd. Tak więc, zmiana słowa wejściowego zmienia częstotliwość strojenia filtra, tak jak potencjometr. Porównaj ten układ z filtrem sterowanym napięciem OTA z rozdziału jedenastego. Koncepcyjnie są one bardzo podobne.

Rysunek ¨(¨PageIndex{16}}): DAC7821. Reprinted courtesy of Texas Instruments
DAC7821
DAC7821 jest dość standardowym 12-bitowym przetwornikiem liniowym i został przedstawiony na rysunku \(\PageIndex{16}}). Jego ciekawymi aspektami jest to, że jest to konwerter mnożący oraz to, że jest kompatybilny z mikroprocesorem. Efekt mnożenia wynika z faktu, że do wysterowania sieci drabinkowej R/2R wykorzystywana jest wartość zadana. Jeśli odniesienie jest zmienione, wyjście jest efektywnie przeskalowane. W związku z tym można myśleć o sygnale wyjściowym jako równym wartości referencyjnej pomnożonej przez cyfrowe słowo wejściowe. Można również myśleć o tym jako o formie „cyfrowej regulacji głośności”.
Dzięki dołączeniu kilku dodatkowych linii logicznych, układ scalony stał się kompatybilny z mikroprocesorem. Oznacza to, że DAC7821 posiada linie chip select oraz odczytu/zapisu wraz z 12 liniami wejściowymi danych. Dzięki temu konwerter może być podłączony bezpośrednio do magistrali danych mikroprocesora. Dzięki zastosowaniu pamięciowo-mapowanych I/O, mikroprocesor może zapisywać dane do konwertera tak samo jak zapisuje dane do pamięci. 16-bitowy system mikroprocesorowy może przedstawić konwerterowi wszystkie dane, których potrzebuje podczas jednego cyklu zapisu, jednak 8-bitowy mikroprocesor będzie potrzebował dwóch cykli zapisu i jakiejś formy zatrzasku. Jeden adres może być użyty dla dolnych 8 bitów, a inny adres dla pozostałych 4 bitów. Uproszczony system jest pokazany na rysunku (\PageIndex{17}) przy użyciu 8-bitowego mikroprocesora.
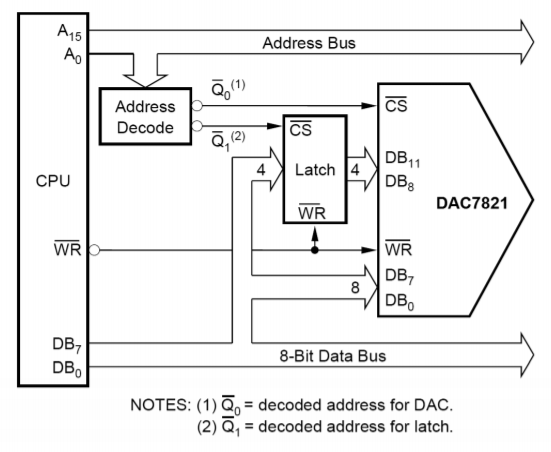
Rysunek (\PageIndex{17}): Interfejs mikroprocesora do przetwornika DAC7821. Przedruk dzięki uprzejmości Texas Instruments
PCM5242
PcM5242 to stereofoniczny 24-bitowy konwerter zaprojektowany specjalnie do wysokiej jakości aplikacji cyfrowego audio. Jest on dostarczany w obudowie VQFN (Very thin Quad Flat No-lead). Schemat blokowy i listę funkcji pokazano na rysunku \(\PageIndex{18a}). W przeciwieństwie do innych konwerterów, PCM5242 posiada szeregowe, a nie równoległe wejście danych. Zawiera on swój własny, wbudowany układ konwersji szeregowej i logiki. Technika ta pozwala na obniżenie kosztów systemu. Jest to również zaskakująco wygodne, ponieważ wiele specjalizowanych układów scalonych do przetwarzania sygnałów cyfrowych, które mogą być używane z PCM5242, wykorzystuje wyjście szeregowe. Może ono być doprowadzone bezpośrednio do układu PCM5242 w formacie 16-, 24- lub 32-bitowym.

Rysunek \(\PageIndex{18a}): PCM5242. Przedruk dzięki uprzejmości firmy Texas Instruments
Specyfikację PCM5242 pokazano na rysunku \(\PageIndex{18b}). Należy zauważyć, że to urządzenie jest wyspecyfikowane dla częstotliwości próbkowania od 48 kHz do 192 kHz. Całkowite zniekształcenia harmoniczne plus szum wynoszą zazwyczaj 94 dB poniżej pełnej skali wyjściowej w przypadku stosowania z dowolną z tych częstotliwości próbkowania. Ze względu na wysoką rozdzielczość i zakres dynamiki 114 dB, należy zachować szczególną ostrożność podczas projektowania obwodów, aby uniknąć zbierania szumów i zakłóceń RF.
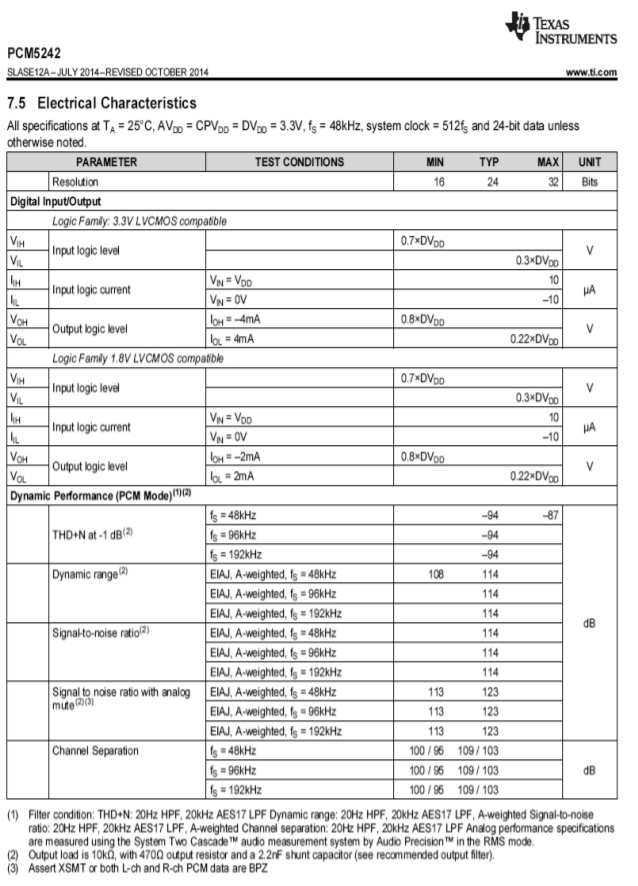
Rysunek \(\): Specyfikacja PCM5242. Przedruk dzięki uprzejmości Texas Instruments
12.4.3: Zastosowania układów scalonych konwerterów cyfrowo-analogowych
Przykład
Prawdopodobnie pierwszą rzeczą, o której myśli wiele osób, gdy słyszy określenia cyfrowy lub zdigitalizowany, jest płyta kompaktowa audio, w skrócie CD. Domowe odtwarzacze CD są doskonałym przykładem zastosowania precyzyjnych układów DA w naszym codziennym życiu. Dane muzyczne zapisywane są na płycie CD z rozdzielczością 16 bitów i częstotliwością próbkowania 44,1 kHz. Daje to częstotliwość Nyquista równą 22,05 kHz, która jest wystarczająco wysoka, aby objąć zakres słyszalności większości ludzi. Na dysku przechowywana jest również korekcja błędów i dane pomocnicze. Dane są zapisywane na dysku w postaci bardzo małych dołków, które są odczytywane przez laser. Sygnał jest następnie przekształcany na wspólną formę logiki elektronicznej, gdzie jest sprawdzany pod kątem błędów i korygowany w razie potrzeby. Strumień danych jest następnie podawany do konwertera DA w celu rekonstrukcji dźwięku. Pojedynczy konwerter może być multipleksowany pomiędzy dwoma kanałami stereo, lub mogą być użyte dwa dedykowane konwertery. W celu poprawy jakości sygnału często stosuje się nadpróbkowanie w zakresie od 2X do 8X. Schemat blokowy systemu jest pokazany na rysunku \(\PageIndex{19}). Część z przetwornikiem cyfrowo-analogowym wydaje się niemal trywialna w porównaniu z niektórymi bardziej wyrafinowanymi elementami.
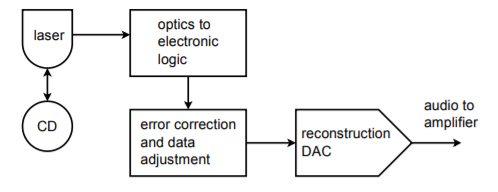
Rysunek \(\PageIndex{19}}): System odtwarzania płyt kompaktowych audio.
Gęstość zapisu optycznej płyty CD jest dość niezwykła. Ten mały dysk (o średnicy mniejszej niż 5 cali) może pomieścić 70 minut muzyki. Ignorując dane pomocnicze, możemy szybko obliczyć całkowitą pamięć. Mamy dwa kanały 16-bitowych danych, czyli 32 bity (4 bajty) na jeden punkt próbkowania. W ciągu 70 minut mamy 44 100 próbek na sekundę, co daje 185,22 megapróbek. Całkowita pamięć danych wynosi 5,927 gigabitów, czyli 741 megabajtów.
Przykład
Jak już wspomnieliśmy, możliwe jest podłączenie przetworników cyfrowo-analogowych bezpośrednio do systemów mikroprocesorowych. Co więcej, mikroprocesor może zapisywać do DAC-a bez większego wysiłku niż zapis do miejsca w pamięci. Mikroprocesor może wypisać do DAC dowolną serię słów danych, jaką sobie zażyczymy i może powtarzać sekwencję praktycznie w nieskończoność. Biorąc pod uwagę tę możliwość, możemy stworzyć generator dowolnych przebiegów. Zamiast być zablokowanym w zestawie predefiniowanych kształtów fal, jak w przypadku zwykłych generatorów funkcyjnych, ten system pozwala na dowolne kształty fal. Dokładność i elastyczność systemu będzie zależeć od jego szybkości i dostępnej rozdzielczości DAC.
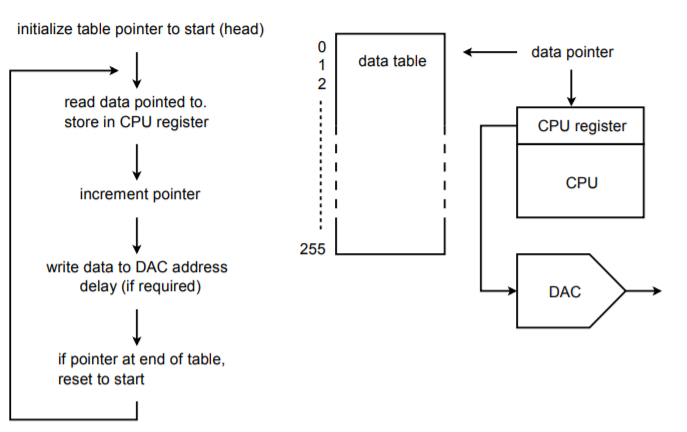
Podstawową ideą jest jedna z tabel wyszukiwania. Dla przykładu, załóżmy, że mamy system 16-bitowy. Stworzymy tablicę wartości danych dla jednego cyklu przebiegu wyjściowego. Dla wygody, rozmiar tablicy może być potęgą 2, np. 256. Innymi słowy, pojedynczy cykl wyjściowy zostanie pocięty na 256 dyskretnych kawałków czasu. Jest więc oczywiste, że konwerter musi być kilkaset razy szybszy niż najwyższa częstotliwość fundamentalna, którą chcemy wytworzyć. Zwiększając lub zmniejszając szybkość danych wyjściowych, możemy zmieniać częstotliwość wyjściowego sygnału fundamentalnego. Jest to znane jako technika zmiennej częstotliwości próbkowania. Możliwa jest również zmiana częstotliwości podstawowej przy użyciu techniki stałej częstotliwości (jest to nieco bardziej skomplikowane, ale oferuje pewne korzyści). Wykres przepływu danych wyjściowych pokazano na rysunku
Rysunek
Rysunek
(\PageIndex{20}}): Generator przebiegów arbitralnych.
Przy inicjalizacji wskaźnik adresowy jest ustawiany na adres początkowy tablicy danych. Procesor odczytuje dane z tablicy za pośrednictwem wskaźnika. Wskaźnik jest inkrementowany tak, że teraz wskazuje na następny element w tablicy. (Niektóre procesory oferują tryb adresowania po inkrementacji, dzięki czemu oba kroki mogą być wykonane w jednej instrukcji). Następnie, procesor zapisuje dane pod specjalny adres DAC. W tym momencie wywoływana jest pewna forma programowego/sprzętowego opóźnienia, która ustawia szybkość danych wyjściowych. Po upływie tego opóźnienia, CPU odczytuje następny element danych poprzez wskaźnik i kontynuuje tak jak w pierwszym przebiegu. Po wysłaniu 256 elementu, wskaźnik jest resetowany do początku tablicy i proces jest kontynuowany. W ten sposób tablica może być traktowana jako okrągła, czyli niekończąca się. Jeśli oprogramowanie systemu jest napisane w języku wyższego poziomu, tablica wskaźników/danych może być zaimplementowana jako prosta tablica, w której indeks tablicy jest ustawiany przez licznik. To nie będzie tak wydajne, jak bezpośrednie podejście na poziomie montażu, choć.
Prawdziwe piękno tego systemu jest to, że tablica danych może zawierać praktycznie dowolną sekwencję danych. Dane mogą reprezentować sinusoidę, impuls, trójkąt lub inną standardową funkcję. Co ważniejsze, dane mogą reprezentować falę sinusoidalną z wbudowanym transjentem szumu, lub równie dobrze sygnał zawierający składową szumową. Dane te mogą pochodzić z trzech podstawowych źródeł. Po pierwsze, tabela danych może być wypełniona poprzez bezpośrednie obliczenia, jeśli znane jest równanie czasoprzestrzenne pożądanej funkcji. Po drugie, dane mogą być wytwarzane przez użytkownika poprzez jakąś formę interakcji z komputerem, być może za pomocą myszki lub bloczka rysunkowego. Wreszcie, dane mogą być uzyskane z sygnału ze świata rzeczywistego. Oznacza to, że do zapisu sygnału w postaci cyfrowej można użyć konwertera analogowo-cyfrowego. Dane te mogą być następnie wczytane do tabeli i odtwarzane wielokrotnie. Generator przebiegów arbitralnych umożliwia użytkownikowi testowanie obwodów i systemów z szeregiem kształtów fal, których wygenerowanie w inny sposób byłoby niemożliwe lub niepraktyczne.
Przykład:
Pod kontrolą komputera, przetworniki DA mogą być stosowane jako część zautomatyzowanego systemu urządzeń testowych. Aby w pełni scharakteryzować produkt elektroniczny, należy wykonać szereg pojedynczych testów. Ustawienie każdego pojedynczego testu może być czasochłonne i obarczone błędem operatora. Zautomatyzowanie tej procedury może poprawić powtarzalność i skrócić czas badań. Istnieje wiele sposobów, w jaki można zautomatyzować ten proces. Przyjrzymy się jednemu z podejść.
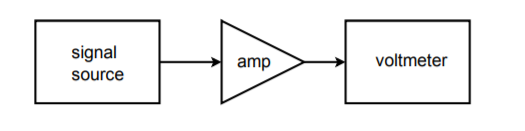
Rysunek ™ (™PageIndex{21}): Prosta konfiguracja testowa.
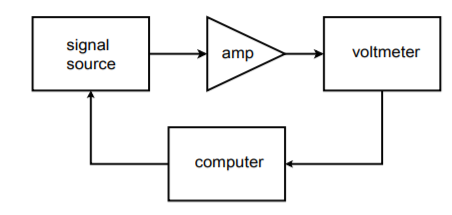
Załóżmy, że chcielibyśmy wykonać pomiary odpowiedzi częstotliwościowej wzmacniacza dla 20 różnych częstotliwości. Układ testowy odpowiedni do tego zadania pokazany jest na rysunku (ÆPageIndex{21}}). Wykonanie tego testu ręcznie wymaga 20 różnych ustawień sygnału źródłowego i 20 odpowiadających im odczytów na wyjściu. Może się to okazać dość żmudne, jeśli testowanych ma być wiele urządzeń. Byłoby bardzo przydatne, gdyby istniał jakiś sposób, w jaki częstotliwość źródłowa mogłaby być automatycznie zmieniana na wstępnie ustawione wartości. Nie jest to szczególnie trudne. Większość nowoczesnych źródeł posiada wejścia napięć sterujących, które mogą być użyte do ustawienia częstotliwości. Wymagane napięcie sterujące może być stworzone i precyzyjnie ustawione poprzez użycie komputera i przetwornika DA. Komputer może być zaprogramowany tak, aby wysyłał określone słowa cyfrowe do przetwornika C/A, który z kolei zasila wejście sterujące źródła sygnału. Innymi słowy, słowo danych bezpośrednio ustawia częstotliwość źródła sygnału. Komputer może być zaprogramowany do wysyłania praktycznie dowolnej sekwencji słów danych z niemal dowolną szybkością i robić to wszystko bez interwencji operatora. Operator musi jedynie uruchomić proces. Powtarzalność testów jest bardzo wysoka przy zastosowaniu takiego systemu. Schemat blokowy tego systemu pokazano na rysunku
Rysunek
Rysunek
(\i1ndex{22}): Automatyczna konfiguracja testu.
W celu rejestracji danych, woltomierz może być podłączony do rejestratora wykresów paskowych, lub jeszcze lepiej, z powrotem do komputera. Dane mogą być przesyłane do komputera w postaci cyfrowej, jeśli woltomierz jest dość zaawansowany konstrukcyjnie, lub, przy zastosowaniu przetwornika analogowo-cyfrowego, sygnał wyjściowy może być bezpośrednio próbkowany i manipulowany przez komputer. W obu przypadkach, pliki danych mogą być tworzone dla każdej testowanej jednostki i przechowywane do późniejszego wykorzystania. Można również szybko przeprowadzić wygodną analizę statystyczną po zakończeniu partii testów. Należy zauważyć, że ponieważ przetwornik DA generuje tylko sygnał sterujący, bardzo wysoka rozdzielczość i niskie zniekształcenia nie są zwykle wymagane. Jeżeli zastosowany jest konwerter o wysokiej rozdzielczości, możliwe jest tworzenie sygnałów testowych w komputerze (jak w generatorze funkcji arbitralnych) i rezygnacja ze źródła sygnału.
Zautomatyzowany system testowy jest tylko jednym z możliwych zastosowań sterowania przyrządami. Innym ciekawym przykładem jest generowanie laserowych „pokazów świetlnych”. Schemat blokowy uproszczonego systemu pokazany jest na rysunku. W celu utworzenia skomplikowanych wzorów widzianych przez publiczność, wiązka laserowa jest odbijana od małych ruchomych lusterek. Lusterka te mogą być zamontowane na czymś tak prostym jak galwanometr. Galwanometr jest zasilany przez przetwornik cyfrowo-analogowy. Wzór, jaki tworzy wiązka laserowa, zależy od tego, jak galwanometr porusza lustrem, co z kolei jest kontrolowane przez słowa danych podawane do przetwornika cyfrowo-analogowego. W praktyce można użyć kilku luster, aby odchylić wiązkę wzdłuż trzech osi.
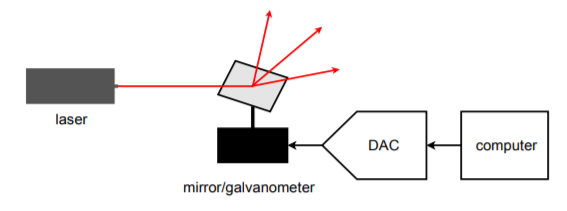
Rysunek \u0026apos;: Oświetlenie sterowane komputerowo.
KonwerteryDA mogą być używane do regulacji dowolnego urządzenia z wejściem typu control-voltage. Mogą być również stosowane do sterowania urządzeniami elektromechanicznymi, które reagują na przyłożone napięcie. Ich prawdziwą zaletą jest powtarzalność i elastyczność, jaką oferują.