Jaka jest różnica między PNP i NPN?

Ten artykuł ukazał się w Microwaves & RF i został opublikowany tutaj za zgodą.

Czego się dowiesz:

• Maksymalna przepustowość kanału jako funkcja szybkości symbolu i szerokości pasma.
• Maksymalna przepustowość kanału w funkcji zakłóceń szumowych.
• Jak rozważania o przepustowości idą aż do użytkownika.

To bardzo łatwa i normalna rzecz, aby skupić się na głównych cechach głównych elementów systemu komunikacyjnego lub łącza, a inne elementy i kwestie traktować jako peryferyjne i nie tak ważne. To, że stało się to zaskakująco dużo w przypadku satelitarnych łączy komunikacyjnych, zwłaszcza tych zdalnych, mobilnych, jest powodem tego listu.

Tutaj jest hipotetyczna sytuacja. Jesteś żołnierzem. Jesteś rozmieszczony w górzystym obszarze Bliskiego Wschodu, niosąc starszy terminal satelitarny Intelsat dla natychmiastowego dostępu z powrotem do kwatery głównej, a kwatera główna wynajęła transponder 72-MHz do wyłącznego użytku.

Miłym, bezpiecznym miejscem jest jaskinia, więc ciągniesz kabel komunikacyjny do terminala satelitarnego przy wejściu do jaskini i siadasz wygodnie, aby zameldować się na swojej stacji roboczej, która jest podłączona do terminala za pomocą modemu QPSK (quadrature phase-shift keying). Meldowanie się jest w porządku, ale komunikacja jest kiepska. Firma satelitarna gwarantuje Ci 72 Mb/s (1 bit na Hz), ale Ty ledwo uzyskujesz mniej niż 35 Mb/s. Czy powinieneś był kupić nowszy terminal? Czy powinieneś używać innego systemu?

Nyquist Maximum Data Rates

Prawdziwą odpowiedzią jest to, co Harry Nyquist i Claude Shannon powiedzieli o maksymalnych prędkościach przesyłu danych przez każdy kanał, włączając w to kabel komunikacyjny. Harry Nyquist zauważył, co zostało dokładnie udokumentowane1, że maksymalna liczba bitów, jaką można uzyskać przez kanał (bez uwzględnienia szumu) wynosi:

Max R = 2 H Log2V

gdzie H jest szerokością pasma kanału, a V jest liczbą dyskretnych symboli (binarne kluczowanie z przesunięciem fazowym, czyli BPSK, wynosi 2, QPSK wynosi 4 itd.)

Jeśli nie jesteś zaznajomiony z log2, nie jest to trudne, gdy się do tego przyzwyczaisz. Log2V jest po prostu wykładnikiem, do którego 2 musi być podniesione, aby równać się V. Tak więc, jeśli V jest BPSK (2), to wyrażenie log2V jest po prostu 1, ponieważ 21 jest w rzeczywistości 2; a jeśli V jest QPSK (4), to wyrażenie log2V jest 2, ponieważ 22 jest w rzeczywistości 4, i tak dalej.

Jeśli używasz kabla 10-MHz Cat 3, wtedy maksymalna prędkość transmisji danych INTO terminala satelitarnego jest BPSK 20 Mb/s, QPSK 40 Mb/s i 8PSK 30 Mb/s, jako funkcja zależności log2. Rysunek 1 pokazuje liczbę stanów i ich log do podstawy 2. Zatem granica Nyquista, przy zastosowaniu modemu QPSK, wynosi 40 Mb/s.

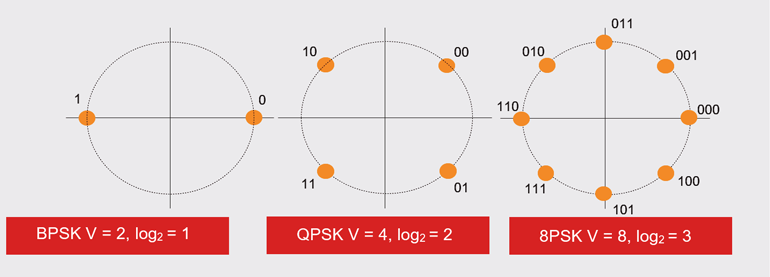1. BPSK, mający dwa stany, ma wartość log2 równą 1; QPSK, mający cztery stany, ma wartość log2 równą 2; i tak dalej.

Shannon Maximum Data Rates

Więc, Harry Nyquist pracował nad zagadnieniem maksymalnych szybkości transmisji danych bez uwzględniania szumu, podczas gdy Claude Shannon pracował nad nim ściśle jako funkcją szumu. Jego równanie2 mówi:

Max R = H log2 (1 + SNR)

gdzie H to ponownie szerokość pasma kanału, a SNR to moc sygnału podzielona przez moc szumu, zazwyczaj podawana w dB. Załóżmy, że współczynnik SNR na tym samym kablu Cat 3 wynosi około 30 dB lub 1000 w liczbach surowych (współczynnik SNR musi zostać przekształcony na wartość racjonalną, aby obliczyć wykładnik). Ponieważ do tej pory zwiększaliśmy skalę wykładników 2, możemy to robić dalej. Rysunek 2 pokazuje tę progresję.

2. Liczba, pokazana na górnej linii, ma wartość wykładniczą, pokazaną na dolnej linii, i demonstruje znaczenie temperatury szumów systemu w odniesieniu do przepustowości kanału.

Jeśli zaokrąglimy trochę dla uproszczenia, 1 001 jest bliżej 1 024 niż jakikolwiek inny przyrost, a 2 podniesione do dziesiątej potęgi daje wartość znacznie bliższą niż jakikolwiek inny wykładnik. Siedząc w swojej jaskini z kablem Cat 3 o szerokości pasma 10-MHz, Claude Shannon mówi, że powinieneś uzyskać szybkość transmisji danych 10 x 106 (10) = 100 Mb/s.

Jeśli Claude Shannon mówi, że możesz uzyskać maksymalną szybkość transmisji danych do terminala komunikacji satelitarnej 100 Mb/s, a Harry Nyquist mówi, że możesz uzyskać tylko 40 Mb/s do i z twojej stacji roboczej wyposażonej w QPSK, kto ma rację?

Spójrzmy na inną analogię. Uniwersytet Notre Dame ma akademicko ograniczoną, ale stosunkowo dobrą drużynę futbolową. Z drugiej strony, ma świetny zespół marszowy, ponieważ wybitni muzycy są często wybitnymi uczniami szkół średnich. Aby dostać się na boisko, zespół musi maszerować przez dwa łuki, z których jeden pozwala na 15 członków na raz, a drugi na 10. Jakich członków w szeregu ustawia się zespół? Cóż, w ten sam sposób Nyquist i Shannon nie rywalizują ze sobą. To tylko dwie różne bramy z dwoma różnymi ograniczeniami.

To nie jest tylko główny system. To są go-intas i go-outas aż do rąk piszących na klawiaturze. A oryginalne prace opublikowane przez fizyka Nyquista3 i matematyka/inżyniera Shannona4 wciąż mają nam coś do powiedzenia.

1. Przykład równania można znaleźć w dowolnym wydaniu Data and Computer Communications autorstwa Williama Stallingsa, wymienionym pod hasłem Nyquist Bandwidth. Uwaga: Różni autorzy używają różnych liter do oznaczania szybkości transmisji danych, szerokości pasma itp.

2. Jak z Nyquist równanie można znaleźć w każdej edycji Data and Computer Communications przez William Stallings, ten jest wymieniony w Shannon Capacity Formula. Uwaga: Różni autorzy używają różnych liter do oznaczania szybkości transmisji danych, szerokości pasma, itp.

3. Niektóre tematy w teorii transmisji telegraficznej (co implikowało limit) zostały przedstawione na Zimowej Konwencji AIEE, Nowy Jork, N.Y., 13-17 lutego 1928. Została ona ponownie opublikowana jako „Classic Paper” w Proceedings of the IEEE w lutym 2002 roku.

4. „Communications in the Presence of Noise” została opublikowana w Proceedings of the IRE w styczniu 1949 roku, dziewięć lat po jej napisaniu.

5.