Obliczanie objętości
Ta strona wyjaśnia, jak obliczyć objętość obiektów stałych, tj. ile można zmieścić w obiekcie, jeśli, na przykład, wypełnił go cieczą.
Objętość jest miarą tego, ile miejsca jest w dwuwymiarowym obiekcie (zobacz naszą stronę: Obliczanie powierzchni, aby dowiedzieć się więcej).
Objętość jest miarą tego, ile miejsca jest w trójwymiarowym obiekcie. Nasza strona na temat trójwymiarowych kształtów wyjaśnia podstawy takich kształtów.
W prawdziwym świecie, obliczanie objętości nie jest prawdopodobnie czymś, co będziesz używał tak często jak obliczanie powierzchni.
Jednakże może to być nadal ważne. Umiejętność obliczania objętości pozwoli ci na przykład określić, ile miejsca do pakowania masz podczas przeprowadzki, ile miejsca w biurze potrzebujesz lub ile dżemu zmieścisz w słoiku.
Może być również przydatna do zrozumienia, co media mają na myśli, gdy mówią o pojemności tamy lub przepływie rzeki.
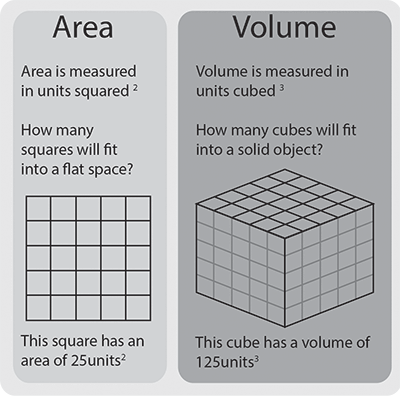
Uwaga na temat jednostek
Powierzchnia jest wyrażana w jednostkach kwadratowych, ponieważ są to dwie miary pomnożone przez siebie.
Objętość jest wyrażana w jednostkach sześciennych, ponieważ jest to suma trzech miar (długości, szerokości i głębokości) pomnożonych przez siebie. Jednostki sześcienne obejmują cm3, m3 i stopy sześcienne.
UWAGA!
Objętość może być również wyrażona jako pojemność cieczy.
System metryczny
W systemie metrycznym pojemność cieczy jest mierzona w litrach, co jest bezpośrednio porównywalne z pomiarem sześciennym, ponieważ 1ml = 1cm3. 1 litr = 1,000 ml = 1,000cm3.
System imperialny/angielski
W systemie imperialnym/angielskim miarami równoważnymi są uncje płynne, pinty, kwarty i galony, których nie da się łatwo przeliczyć na stopy sześcienne. Dlatego najlepiej jest trzymać się jednostek objętości cieczy lub ciała stałego.
Po więcej, zobacz naszą stronę na temat systemów miar
Podstawowe wzory na obliczanie objętości
Objętość ciał stałych opartych na prostokątach

Podstawowym wzorem na pole powierzchni bryły prostokątnej jest długość × szerokość, natomiast podstawowym wzorem na objętość jest długość × szerokość × wysokość.
To, jak odnosimy się do różnych wymiarów, nie zmienia sposobu obliczania: można na przykład użyć „głębokości” zamiast „wysokości”. Ważne jest, że te trzy wymiary są mnożone razem. Możesz mnożyć w dowolnej kolejności, ponieważ nie zmieni to odpowiedzi (zobacz naszą stronę o mnożeniu, aby dowiedzieć się więcej).
Pudełko o wymiarach 15cm szerokości, 25cm długości i 5 cm wysokości ma objętość:
15 × 25 × 5 = 1875cm3
Objętość graniastosłupów i walców
Ten podstawowy wzór może być rozszerzony, aby objąć objętość walców i graniastosłupów. Zamiast prostokątnego końca mamy po prostu inny kształt: koło dla cylindrów, trójkąt, sześciokąt lub jakikolwiek inny wielokąt dla graniastosłupów.
W przypadku cylindrów i pryzmatów objętość jest polem powierzchni jednego boku pomnożonym przez głębokość lub wysokość kształtu.
Podstawowy wzór na objętość pryzmatów i cylindrów to zatem:
Powierzchnia końca × wysokość/głębokość graniastosłupa/cylindra.
Objętość stożków i ostrosłupów
Ta sama zasada jak powyżej (szerokość × długość × wysokość) obowiązuje przy obliczaniu objętości stożka lub ostrosłupa, z wyjątkiem tego, że ponieważ dochodzą one do punktu, objętość jest tylko częścią tego, co byłoby, gdyby nadal miały ten sam kształt.
Objętość stożka lub ostrosłupa jest dokładnie jedną trzecią tego, co byłoby dla pudełka lub cylindra o tej samej podstawie.
Wzór jest zatem następujący:
Powierzchnia podstawy lub kształtu końcowego × wysokość stożka/piramidy × 1/3
Powróć do naszej strony Obliczanie pola powierzchni, jeśli nie pamiętasz jak obliczyć pole koła lub trójkąta.
Na przykład, aby obliczyć objętość stożka o promieniu 5 cm i wysokości 10 cm:
Powierzchnia okręgu = πr2 (gdzie π (pi) wynosi około 3,14, a r to promień okręgu).
W tym przykładzie, pole podstawy (okręgu) = πr2 = 3,14 × 5 × 5 = 78,5cm2.
78,5 × 10 = 785
785 × 1/3 = 261,6667cm3

Objętość kuli
Tak jak w przypadku okręgu, potrzebujesz π (pi), aby obliczyć objętość kuli.
Wzór to 4/3 × π × promień3.
Możesz się zastanawiać, w jaki sposób mógłbyś obliczyć promień kuli. Zamiast wbijać w nią igłę do robótek na drutach (skuteczne, ale niebezpieczne dla piłki!), istnieje prostszy sposób.
Możesz zmierzyć odległość wokół najszerszego punktu kuli bezpośrednio, na przykład za pomocą taśmy mierniczej. Okrąg ten jest obwodem i ma taki sam promień jak sama kula.
Obwód okręgu obliczamy jako 2 x π x promień.
Aby obliczyć promień z obwodu:
Podziel obwód przez (2 x π).
Przykłady praktyczne: Obliczanie objętości
Przykład 1

Oblicz objętość walca o długości 20cm, którego okrągły koniec ma promień 2,5cm.
Najpierw należy obliczyć pole powierzchni jednego z okrągłych końców walca.
Pole powierzchni koła wynosi πr2 (π × promień × promień). π (pi) wynosi w przybliżeniu 3,14.
Pole powierzchni jednego z końców wynosi więc:
3,14 x 2,5 x 2,5 = 19,63cm2
Objętość to pole powierzchni jednego z końców pomnożone przez długość, wynosi więc:
19.63cm2 x 20cm = 392,70cm3

Przykład 2
Który z nich jest większy objętościowo, kula o promieniu 2cm czy ostrosłup o podstawie kwadratu 2,5cm i wysokości 10cm?
Najpierw należy obliczyć objętość kuli.
Objętość kuli to 4/3 × π × promień3.
Objętość kuli wynosi więc:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51cm3
Potem oblicz objętość ostrosłupa.
Objętość ostrosłupa to 1/3 × pole podstawy × wysokość.
Powierzchnia podstawy = długość × szerokość = 2,5cm × 2,5cm = 6,25cm2
Objętość wynosi więc 1/3 x 6,25 × 10 = 20,83cm3
Kula jest więc większa objętościowo od ostrosłupa.
Obliczanie objętości brył nieregularnych
Tak jak możesz obliczyć pole powierzchni nieregularnych dwuwymiarowych kształtów poprzez rozbicie ich na regularne, możesz zrobić to samo, aby obliczyć objętość nieregularnych brył. Po prostu podziel bryłę na mniejsze części, aż osiągniesz tylko bryły, z którymi możesz łatwo pracować.
Przykład praktyczny
Oblicz objętość cylindra z wodą o całkowitej wysokości 1m, średnicy 40cm, którego górna część jest półsferyczna.

Pierw dzielimy kształt na dwie części, walec i półsferę (połowę kuli).
Objętość kuli wynosi 4/3 × π × promień3. W tym przykładzie promień wynosi 20cm (połowa średnicy). Ponieważ wierzchołek jest półsferyczny, jego objętość będzie o połowę mniejsza od objętości pełnej kuli. Objętość tej części kształtu wynosi zatem:
0,5 × 4/3 × π × 203 = 16 755,16cm3
Objętość walca to pole powierzchni podstawy × wysokość. Tutaj wysokość walca jest wysokością całkowitą pomniejszoną o promień kuli, czyli 1m – 20cm = 80cm. Pole podstawy wynosi πr2.
Objętość przekroju walca o tym kształcie wynosi więc:
80 × π × 20 × 20 = 100 530,96cm3
Całkowita objętość tego pojemnika na wodę wynosi więc:
100 530,96 + 16 755,16 = 117 286,12cm3.
Jest to dość duża liczba, więc być może wolisz ją przeliczyć na 117,19 litra, dzieląc przez 1000 (bo w litrze jest 1000cm3). Jednak wyrażenie tego w cm3 jest całkiem poprawne, ponieważ zadanie nie wymaga, aby odpowiedź była wyrażona w jakiejś szczególnej formie.
W podsumowaniu…
Używając tych zasad, jeśli to konieczne, powinieneś teraz być w stanie obliczyć objętość prawie wszystkiego w swoim życiu, czy to skrzyni do pakowania, pokoju, czy butli z wodą.