Tetrahedron

Spis treści

W Cuemath wierzymy, że matematyka jest umiejętnością życiową. Nasi eksperci matematyczni skupiają się na „Dlaczego” za „Co”. Uczniowie mogą korzystać z szerokiej gamy interaktywnych arkuszy, wizualizacji, symulacji, testów praktycznych i innych, aby zrozumieć koncepcję dogłębnie.

Zarezerwuj BEZPŁATNĄ klasę próbną już dziś! i doświadcz LIVE Online Class Cuemath ze swoim dzieckiem.

Tetrahedron jest jedną z pięciu brył platońskich.

Ma trójkąty jako swoje ściany.

Czworościan to trójwymiarowa bryła, której wszystkie ściany są trójkątami.

Siatka czworościanu foremnego

Zróbmy małe ćwiczenie.

Podajemy kartkę papieru.

Możesz zaobserwować dwie różne siatki czworościanu foremnego pokazane poniżej.

Kopiujemy to na kartkę papieru.

Przecinamy wzdłuż krawędzi i składamy zgodnie z rysunkiem poniżej.

Złożony papier tworzy czworościan.

Poniższa symulacja ilustruje czworościan w 3D.

Kliknij na krawędź czworościanu i przeciągnij ją dookoła.

Co widzisz?

Będziesz mógł zobaczyć wszystkie 4 ściany czworościanu, gdy będzie się on obracał.

Zwykły czworościan ma trójkąty równoboczne jako swoje ściany.

Ponieważ jest on zbudowany z trójkątów równobocznych, wszystkie kąty wewnętrzne czworościanu będą miały miarę ∗(60^)

Czworościan nieregularny również ma trójkątne ściany, ale nie są one równoboczne.

Kąty wewnętrzne czworościanu w każdej płaszczyźnie sumują się do 180, ponieważ są trójkątne.

Jeśli czworościan nie jest wyraźnie wymieniony jako nieregularny, domyślnie przyjmuje się, że wszystkie czworościany są czworościanami foremnymi.

• Ma 4 ściany, 6 krawędzi i 4 rogi.
• Wszystkie cztery wierzchołki są jednakowo odległe od siebie.
• W każdym z wierzchołków spotykają się 3 krawędzie.
• Ma 6 płaszczyzn symetrii.
• W przeciwieństwie do innych brył platońskich, czworościan nie ma ścian równoległych.
• Czworościan foremny ma trójkąty równoboczne na wszystkich ścianach.

Różne wzory na czworościan są wymienione poniżej.

Rozważmy czworościan foremny zbudowany z trójkątów równobocznych o boku s.

Objętość czworościanu:

(\tekst{Volume} = \frac{s^3}{6\sqrt{2}}})

Całkowita powierzchnia czworościanu:

(\tekst{TSA} = \sqrt{3} \:s^2 \)

Powierzchnia jednej ściany czworościanu:

(\text{Powierzchnia ściany } = \frac { \sqrt{3}}{4}s^2 \)

Wysokość „s” czworościanu:

\(\text{ Wysokość skośna} = \frac {sqrt{3}}{2}s^2 \))

Wysokość 'h' czworościanu:

\(\tekst{ Wysokość} = \frac {sqrt{6}}{3}}})

Użyj kalkulatora czworościanu, aby znaleźć objętość i powierzchnię całkowitą.

Wprowadź długość krawędzi w kalkulatorze poniżej.

Pomóż swojemu dziecku uzyskać wyższe wyniki dzięki autorskiemu DARMOWEMU testowi diagnostycznemu Cuemath. Uzyskaj dostęp do szczegółowych raportów, spersonalizowanych planów nauczania i BEZPŁATNEJ sesji doradczej. Rozwiąż test już teraz.

Przykład 1

Dwa przystające czworościany sklejono wzdłuż ich podstawy, tworząc dwupiramidę trójkątną.

Ile ścian, krawędzi i wierzchołków ma ta piramida?

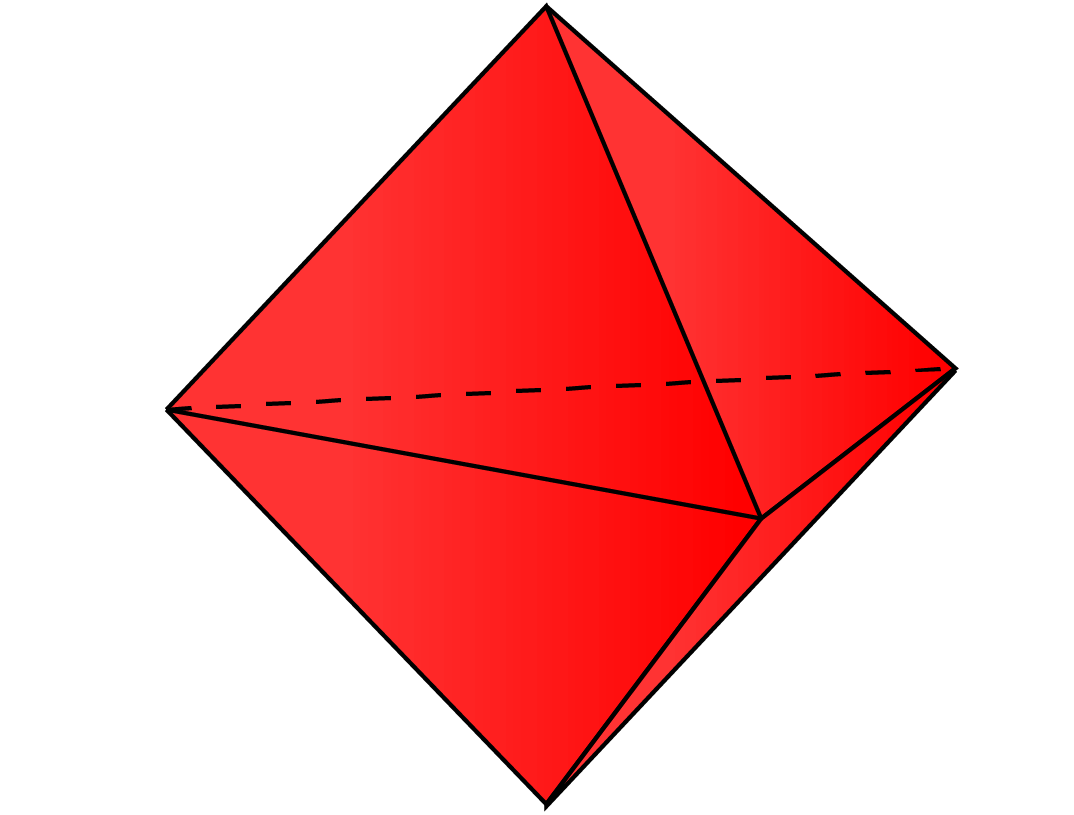
Rozwiązanie:

Jeśli otworzymy powyższy obrazek, aby zobaczyć siatkę dwunastościanu trójkątnego, to zauważymy, że:

Jest 6 trójkątnych ścian, 9 krawędzi i 5 wierzchołków.

Dwupiramida trójkątna ma 6 trójkątnych ścian, 9 krawędzi i 5 wierzchołków.

Przykład 2

Znajdź objętość czworościanu foremnego o boku długości 5 jednostek.

(Odpowiedź zaokrąglij do 2 miejsc po przecinku)

Rozwiązanie:

Wiemy, że objętość czworościanu, którego bok ma długość wynosi:

(^in{align}}}text{Volume} = \frac{s^3}{6\sqrt{2}}}}end{align}})

Wiemy, że objętość czworościanu, którego bok \(s) jest długością krawędzi, wynosi.

Podstawiając ∗ jako 5 otrzymujemy

Objętość czworościanu foremnego wynosi 14.73 jednostek3

Przykład 3

Każda krawędź czworościanu foremnego ma długość 6 jednostek.

Znajdź jego pole powierzchni całkowitej.

Rozwiązanie:

Całkowite pole powierzchni czworościanu foremnego o boku ^2

Tekst{TSA} = ^sqrt{3} ^:s^2 \)

Substituting s = 6, we get

Total Surface Area = 62.35 jednostek2

Przykład 4

Suma długości krawędzi czworościanu foremnego wynosi 60 jednostek.

Znajdź pole powierzchni jednej z jego ścian.

Rozwiązanie:

Wiemy, że czworościan foremny ma 6 krawędzi.

Długość każdej krawędzi wynosi zatem:

(∗frac{60}{6} = 10 ∗tekst{jednostek}}}end{align})

Powierzchnia jednej ściany czworościanu foremnego:

Podstawiając s = 10, otrzymujemy:

Powierzchnia jednej z jego ścian = 8.66 jednostek2

Przykład 5

Dla jakiej miary krawędzi pole powierzchni całkowitej czworościanu foremnego jest równe jego objętości?

Rozwiązanie:

Wiemy, że \(\tekst{TSA} = \sqrt{3} \:s^2 \) oraz \(\begin{align}}text{Volume} = \frac{s^3}{6\sqrt{2}}} \end{align}})

Jeśli TSA = Volume, możemy powiedzieć, że:

( \sqrt{3} \:s^2 = \frac{s^3}{6\sqrt{2}})

Rozwiązując dla s, mamy

Długość krawędzi czworościanu foremnego wynosi \(6\sqrt6)