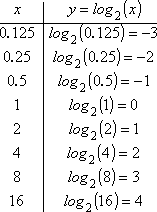Wykresy funkcji logarytmicznych: Wprowadzenie
Powrót do indeksu lekcji | Wykonaj lekcje w kolejności | Strona przyjazna do drukowania
Wykresy funkcji logarytmicznych: Intro (strona 1 z 3)
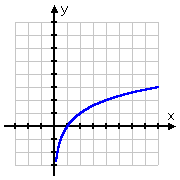
Z natury logarytmu, większość wykresów logarytmicznych ma ten sam kształt, podobny do wykresu pierwiastka kwadratowego:
| y = sqrt(x) | y = log2(x) |
 |
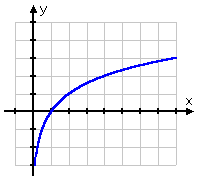 |
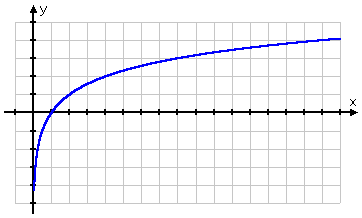
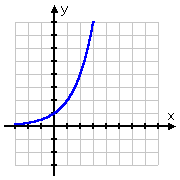
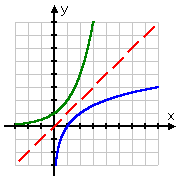
Wykres pierwiastka kwadratowego zaczyna się w punkcie (0, 0), a następnie odchodzi w prawo. Z drugiej strony, wykres logu przechodzi przez (1, 0), odchodząc w prawo, ale także przesuwając się w dół po dodatniej stronie osi y. Pamiętając, że logi są odwrotnościami wykładników, taki kształt wykresu logarytmicznego ma sens: wykres logarytmu, będąc odwrotnością wykładnika, byłby po prostu „odwróceniem” wykresu wykładniczego:
| y = 2x | y = log2(x) |
 |
 |
| porównanie dwóch wykresów, pokazując linię inwersji na czerwono |
|
 |
|
Wykres wykładników jest dość prosty. Na przykład, aby wykreślić wykres y = 2x, wystarczy wstawić kilka wartości dla x, obliczyć odpowiadające im wartości y i wykreślić punkty. Ale jak wykreślić wykres logarytmów? Istnieją dwie możliwości. Oto pierwsza z nich: Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
- Wykres y = log2(x).
- Ponieważ 20 = 1, to log2(1) = 0, a (1, 0) jest na wykresie.
- Skoro 21 = 2, to log2(2) = 1, a (2, 1) jest na wykresie.
- Ponieważ 3 nie jest potęgą 2, to log2(3) będzie jakąś niechlujną wartością. Więc nie będę sobie zawracał głowy wykresem x = 3.
- Skoro 22 = 4, to log2(4) = 2, a (4, 2) jest na wykresie.
- Ponieważ 5, 6 i 7 też nie są potęgami 2, pominę je i przejdę do x = 8.
- Ponieważ 23 = 8, to log2(8) = 3, więc (8, 3) jest na wykresie.
- Następną potęgą 2 jest 16: ponieważ 24 = 16, to log2(16) = 4, a (16, 4) jest na wykresie.
- Następna potęga 2, x = 32, jest zbyt duża jak na mój gust; nie mam ochoty rysować mojego wykresu tak szeroko, więc zrezygnuję z x = 16.
Aby wykreślić ten wykres „ręcznie”, muszę najpierw pamiętać, że logi nie są zdefiniowane dla ujemnych wartości x lub dla x = 0. Z powodu tego ograniczenia na dziedzinę (wartości wejściowe) logu, nie będę nawet próbował znaleźć wartości y dla, powiedzmy, x = -3 lub x = 0. Zamiast tego zacznę od x = 1 i będę pracował stamtąd, używając definicji logu.
Powyższe daje mi punkt (1, 0) i kilka punktów po prawej stronie, ale co mam zrobić dla wartości x między 0 a 1? W przypadku tego przedziału muszę myśleć w kategoriach ujemnych potęg i wzajemności. Tak jak lewa „połówka” funkcji wykładniczej ma niewiele punktów, które można przedstawić na wykresie (reszta z nich jest zbyt blisko osi x), tak samo dolna „połówka” funkcji logarytmicznej ma niewiele punktów, które można przedstawić na wykresie, reszta z nich jest zbyt blisko osi y. Ale mogę znaleźć kilka:
Skoro 2-1 = 1/2 = 0.5, to log2(0.5) = -1, a (0.5, -1) jest na wykresie.
Skoro 2-2 = 1/4 = 0.25, to log2(0.25) = -2, a (0.25, -2) jest na wykresie.
Skoro 2-3 = 1/8 = 0.125, to log2(0.125) = -3, a (0.125, -3) znajduje się na wykresie.
Kolejna potęga 2 (gdy x porusza się w tym kierunku) to 1/16 = 2-4, ale wartość x dla punktu (0.0625, -4) wydaje się zbyt mała, aby zawracać sobie nią głowę, więc zakończę z punktami, które już znalazłem.
|
Listowanie tych punktów daje mi mój wykres T: |
|
|
|
Rysując moje kropki, a następnie szkicując w linii (pamiętając, aby nie iść na lewo od osi y!), otrzymam ten wykres: |
|
Top | 1 | 2 | 3 | Return to Index Next >>
|
Cite this article as: |
Stapel, Elizabeth. „Graphing Logarithmic Functions: Intro.” Purplemath. Dostępne od 2016
|