Cálculo de Volume
Esta página explica como calcular o volume de objectos sólidos, ou seja, quanto poderia caber num objecto se, por exemplo, o enchesse com um líquido.
Area é a medida de quanto espaço existe dentro de um objecto bidimensional (ver a nossa página: Área de Cálculo para mais).
Volume é a medida de quanto espaço existe dentro de um objecto tridimensional. A nossa página sobre formas tridimensionais explica o básico de tais formas.
No mundo real, calcular volume provavelmente não é algo que se utilize tão frequentemente como calcular área.
No entanto, ainda pode ser importante. Ser capaz de calcular volume permitir-lhe-á, por exemplo, calcular quanto espaço de embalagem tem ao mudar de casa, quanto espaço de escritório precisa, ou quanta compota pode caber num frasco.
Também pode ser útil para compreender o que os meios de comunicação significam quando falam da capacidade de uma barragem ou do caudal de um rio.
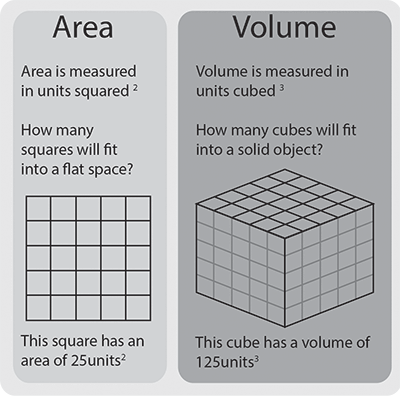
Uma nota sobre Unidades
Area é expressa em unidades quadradas, porque são duas medidas multiplicadas em conjunto.
Volume é expresso em unidades cúbicas, porque é a soma de três medidas (comprimento, largura e profundidade) multiplicadas em conjunto. As unidades cúbicas incluem cm3, m3 e pés cúbicos.
Aviso!
Volume também pode ser expresso como capacidade líquida.
Sistema métrico
No sistema métrico a capacidade líquida é medida em litros, o que é directamente comparável com a medida cúbica, uma vez que 1ml = 1cm3. 1 litro = 1.000 ml = 1.000cm3.
Sistema Imperial/Inglês
No sistema imperial/Inglês as medidas equivalentes são onças fluidas, pints, quarts e galões, que não são facilmente traduzidas em pés cúbicos. Por conseguinte, é melhor aderir a unidades de volume líquido ou sólido.
Para mais, ver a nossa página sobre Sistemas de Medição
Fórmulas Básicas para Cálculo de Volume
Volume de Sólidos à Base de Rectângulo

Onde a fórmula básica para a área de uma forma rectangular é comprimento × largura, a fórmula básica para o volume é comprimento × largura × altura.
Como se refere às diferentes dimensões não altera o cálculo: pode, por exemplo, utilizar ‘profundidade’ em vez de ‘altura’. O importante é que as três dimensões sejam multiplicadas em conjunto. Pode multiplicar sempre que quiser, pois não altera a resposta (ver a nossa página sobre multiplicação para mais).
Uma caixa com as dimensões 15 cm de largura, 25 cm de comprimento e 5 cm de altura tem um volume de:
15 × 25 × 5 = 1875cm3
Volume de Prismas e Cilindros
Esta fórmula básica pode ser alargada para cobrir também o volume de cilindros e prismas. Em vez de uma extremidade rectangular, simplesmente tem outra forma: um círculo para cilindros, um triângulo, hexágono ou, de facto, qualquer outro polígono para um prisma.
Fectivamente, para cilindros e prismas, o volume é a área de um lado multiplicada pela profundidade ou altura da forma.
A fórmula básica para o volume de prismas e cilindros é portanto:
Área da forma da extremidade × a altura/profundidade do prisma/cilindro.
Volume de Cones e Pirâmides
O mesmo princípio acima (largura × comprimento × altura) aplica-se ao cálculo do volume de um cone ou de uma pirâmide, excepto que, por chegarem a um ponto, o volume é apenas uma proporção do total que seria se continuassem na mesma forma até ao fim.
O volume de um cone ou pirâmide é exactamente um terço do que seria para uma caixa ou cilindro com a mesma base.
A fórmula é portanto:
Área da base ou forma final × a altura do cone/piramide × 1/3
Refer de volta à nossa página Área de Cálculo se não se lembrar como calcular a área de um círculo ou triângulo.
Por exemplo, para calcular o volume de um cone com um raio de 5cm e uma altura de 10cm:
A área dentro de um círculo = πr2 (onde π (pi) é aproximadamente 3,14 e r é o raio do círculo).
Neste exemplo, área da base (círculo) = πr2 = 3,14 × 5 × 5 = 78,5cm2.
78,5 × 10 = 785
785 × 1/3 = 261,6667cm3

Volume de uma Esfera
Como com um círculo, é necessário π (pi) para calcular o volume de uma esfera.
A fórmula é 4/3 × π × raio3.
Pode estar a perguntar-se como se poderia calcular o raio de uma esfera. A menos de espetar uma agulha de tricô através dela (eficaz, mas terminal para a bola!), há uma forma mais simples.
É possível medir directamente a distância em torno do ponto mais largo da esfera, por exemplo, com uma fita métrica. Este círculo é a circunferência e tem o mesmo raio que a própria esfera.
A circunferência de um círculo é calculada como 2 x π x raio.
Para calcular o raio a partir da circunferência você:
Dividir a circunferência por (2 x π).
Exemplos trabalhados: Cálculo do volume
Exemplo 1

Calcular o volume de um cilindro com um comprimento de 20cm, e cuja extremidade circular tem um raio de 2,5cm.
P>Primeiro, calcular a área de uma das extremidades circulares do cilindro.
A área de um círculo é πr2 (π × raio × raio). π (pi) é aproximadamente 3,14.
A área de uma extremidade é portanto:
3,14 x 2,5 x 2,5 = 19,63cm2
O volume é a área de uma extremidade multiplicada pelo comprimento, e é portanto:
19.63cm2 x 20cm = 392,70cm3

Exemplo 2
que é maior em volume, uma esfera com raio 2cm ou uma pirâmide com base 2,5cm e altura de 10cm?
P>Primeiro, calcula o volume da esfera.
O volume de uma esfera é 4/3 × π × raio3.
O volume da esfera é portanto:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51cm3
Em seguida, calcular o volume da pirâmide.
O volume de uma pirâmide é 1/3 × área de base × altura.
Área da base = comprimento × largura = 2,5cm × 2,5cm = 6,25cm2
Volume é portanto 1/3 x 6,25 × 10 = 20,83cm3
A esfera é portanto maior em volume do que a pirâmide.
Cálculo do volume de sólidos irregulares
P>Apenas como se pode calcular a área de formas bidimensionais irregulares dividindo-as em regulares, pode-se fazer o mesmo para calcular o volume de sólidos irregulares. Basta dividir o sólido em partes mais pequenas até se atingir apenas sólidos com os quais se possa trabalhar facilmente.
Exemplo trabalhado
Calcular o volume de um cilindro de água com altura total de 1m, diâmetro de 40cm, e cuja secção superior é semi-esférica.

Divide-se primeiro a forma em duas secções, um cilindro e uma semi-esfera (meia esfera).
O volume de uma esfera é 4/3 × π × raio3. Neste exemplo, o raio é de 20cm (metade do diâmetro). Como o topo é semi-esférico, o seu volume será metade do de uma esfera completa. O volume desta secção da forma portanto:
0,5 × 4/3 × π × 203 = 16.755,16cm3
O volume de um cilindro é a área da base × altura. Aqui, a altura do cilindro é a altura total menos o raio da esfera, que é 1m – 20cm = 80cm. A área da base é πr2.
O volume da secção cilíndrica desta forma é portanto:
80 × π × 20 × 20 = 100,530.96cm3
O volume total deste recipiente de água é portanto:
100,530.96 + 16,755.16 = 117,286.12cm3.
Este é um número bastante grande, pelo que poderá preferir convertê-lo para 117,19 litros dividindo por 1.000 (uma vez que existem 1000cm3 num litro). Contudo, é bastante correcto expressá-lo como cm3, uma vez que o problema não pede que a resposta seja expressa sob qualquer forma particular.
Em Conclusão…
Usando estes princípios, se necessário, deverá agora ser capaz de calcular o volume de quase tudo na sua vida, quer seja uma caixa de embalagem, uma sala, ou um cilindro de água.