Como Compreender Base (Álgebra Linear)

quando se ensina álgebra linear, o conceito de uma base é frequentemente ignorado. Os meus alunos de tutoria podiam compreender a independência linear e o alcance, mas viram a base de como se pode ver um OVNI: confuso e estrangeiro. E isso não é bom, porque a base funciona como ponto de partida para grande parte da álgebra linear.

Precisamos sempre de um ponto de partida, uma base a partir da qual se possa construir tudo o resto. As palavras não podem ser escritas sem a fundação de um alfabeto. As civilizações antigas acreditavam que o universo era formado a partir de 4 elementos clássicos – água, terra, fogo, e ar (há muito tempo…). E os espaços vectoriais, o lar natural da álgebra linear, têm a base como fundamento.

I’m going to explain the basis conceptually using an analogy to painting. Esta analogia foi utilizada em dois artigos anteriores para explicar dois outros conceitos da álgebra linear denominados independência/dependência linear e extensão. Recomendo a leitura desses artigos primeiro, porque ambos os conceitos surgirão mais tarde.

A Base das Cores da Pintura

Em vez de fazer contas, suponha que é um pintor, pronto para pintar uma obra-prima na sua tela. Primeiro, precisa de comprar alguma tinta. Quantas cores deve comprar?

Obviamente, é uma má ideia fazer uma pintura conduzindo até Home Depot e comprando uma lata de tinta cada uma para todos os milhares de cores que têm. Não precisa de trinta tons diferentes de azul, desde o azul azul azulado, até ao azul da montanha, até ao azul da vitória (ideia: criar uma tinta chamada “Defeat Blue”). Só precisa de comprar tinta azul e algumas outras cores.

Se for um pintor mesquinho, poderá até dizer que só precisa de comprar 5 cores para fazer uma pintura: vermelho, amarelo, azul, branco, e preto. Claro, verde seria bom, e rosa seria fixe, mas não precisa de comprar tinta rosa e verde. Afinal, pode combinar tinta vermelha e branca para fazer tinta rosa, ou amarela e azul para fazer verde.

p>vermelho, amarelo, azul, branco, e preto são o conjunto mínimo de cores de que precisa para fazer qualquer outra cor. Poderíamos dizer que estas 5 cores formam uma base para todo o espectro de cores.

Desde que se possa fazer qualquer outra cor usando misturas destas cinco cores, poderíamos dizer que estas cinco cores abrangem o conjunto de todas as cores. Além disso, cada cor do conjunto é necessária: é necessária tinta branca porque nenhuma quantidade de tinta amarela, vermelha, preta, ou azul misturada irá alguma vez criar tinta branca. Por outras palavras, vermelho, amarelo, azul, branco, e preto são independentes um do outro.

Deixe chamar o seu conjunto de tintas à sua paleta. Para que a sua paleta forme uma base para todas as cores, duas condições têm de ser verdadeiras:

1. A paleta abrange o conjunto de todas as cores.
2. Todas as cores da paleta são independentes uma da outra.

Vimos que o vermelho, amarelo, azul, branco, e preto preenchem ambas as condições. Pelo contrário, aqui estão exemplos de paletas que não são bases:

• Vermelho, azul, branco. Isto viola a condição 1. Este conjunto não abrange todas as cores. Muitas cores como amarelo ou verde são impossíveis de fazer com as cores deste conjunto.
• Vermelho, laranja, amarelo, verde, azul, púrpura, branco, preto. Isto viola a condição 2. Estas cores abrangem certamente todas as cores, mas não são independentes. O roxo é uma combinação de vermelho e azul, o verde uma combinação de amarelo e azul, e assim por diante.

As bases de um Espaço Vectorial

Espaços vectoriais são mais abstractos do que as pinturas, mas utilizam a base de forma semelhante. Um espaço vectorial é um conjunto de vectores onde se podem adicionar vectores em conjunto e escalá-los. Por exemplo, o plano 2-D (também conhecido como R²) é um espaço vectorial. É o conjunto de todos os vectores “bidimensionais”, que podem ser pensados como vectores com uma coordenada x e uma coordenada y.

Apenas como criámos uma base para o conjunto de todas as cores, podemos criar um conjunto de vectores que formam uma base de R². Os requisitos de base são quase os mesmos que a nossa base de cores.

Basis: Um conjunto de n vectores, {v₁, v₂,… vₙ}, é uma base de algum espaço S se estas duas condições forem verdadeiras:

1. {v₁, v₂, …vₙ} são linearmente independentes.
2. {v₁, v₂,…vₙ} abrangem o conjunto S. Por outras palavras, Span{v₁,v₂,…vₙ}=S

Por exemplo, pegue nos vectores (0,1) e (1,0), grafados abaixo a verde. Estes vectores são linearmente independentes, uma vez que não há forma de escala (0,1) em (1,0). Além disso, estes dois vectores abrangem todo o plano 2-D, porque é possível reescrever qualquer ponto no espaço 2-D como uma combinação linear de (0,1) e (1,0):

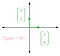
(0,1) e (1,0) formam portanto uma base de R² (Esta base específica de (0,1) e (1,0) é chamada a base padrão). No entanto, esta não é a única base de R² possível. Veja os vectores (1,1) e (-1,1), abaixo indicados. Os vectores cor-de-rosa representam algumas combinações lineares diferentes:

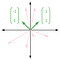
Estes dois vectores são também linearmente independentes, uma vez que não se pode dimensionar um vector para o outro. A partir das combinações lineares rosa, é também claro que (1,1) e (-1,1) abrange todo o R². Portanto, (1,1) e (-1,1) formam outra base para R².

Este é um ponto em que os espaços vectoriais são muito diferentes da analogia da tinta. Com cores de tinta, temos realmente apenas a base de amarelo, azul, vermelho, preto, e branco. Mas no mundo dos espaços vectoriais, qualquer espaço tem um número infinito de bases por onde escolher. Em geral, uma base é o menor conjunto possível de vectores que pode abranger um espaço. É o equivalente vectorial de ser mesquinho com a sua pintura, e apenas comprar as cores mínimas de que necessita.

A base também nos ajuda a descobrir a estrutura subjacente de um espaço vectorial. Por exemplo, sabemos que qualquer base de R² será feita exactamente de dois vectores, como as duas bases que encontrámos anteriormente. Em geral:

• Para algum espaço S, todas as bases de S têm o mesmo número de vectores. Isto foi provado pela primeira vez por Georg Hamel. Se uma base para S é composta por 4 vectores, então qualquer base para S é composta por 4 vectores.
• Uma base para um espaço Rⁿ é composta por n vectores. Qualquer base para R³ (espaço tridimensional) é constituída por 3 vectores. Qualquer base para R⁵ (espaço 5-dimensional, não perguntar) é constituída por 5 vectores.

Porque é que a Base Importa (Transformações Lineares)

Sua própria, a base não tem muito impacto. No entanto, vamos tocar brevemente na razão pela qual a base é tão importante para a álgebra linear.

Podemos pegar num espaço vectorial e transformá-lo, “transformar” aqui significando esticar, virar, ou rodar o espaço. Quando se trabalha com álgebra linear, transformar um espaço vectorial é tão comum como respirar. Suponhamos que eu quero transformar o gráfico A em gráfico B:

Cada gráfico tem a sua própria base (os vectores rosa e azul). É importante notar que tanto o gráfico A como o gráfico B são apenas duas formas diferentes de representar exactamente o mesmo espaço utilizando bases diferentes. É como ler o mesmo livro mas em duas línguas diferentes, como o espanhol e o francês.

A mudança do gráfico A para o gráfico B é chamada uma transformação linear do gráfico. Uma transformação linear actua como um tradutor: Pega em cada ponto do gráfico B e move-o para cada ponto correspondente do gráfico A. Pega na palavra francesa e move-o para o espanhol. No entanto, estamos agora a entrar no mundo das transformações lineares, e isso pode ser explicado noutra altura.

Conclusão

Temos agora uma compreensão mais profunda de três conceitos de álgebra linear: base, independência/dependência linear, e extensão. Estes conceitos são fundamentais para a álgebra linear. A independência/dependência linear diz-lhe quais os vectores que são necessários num conjunto de vectores. Span diz-lhe todas as combinações possíveis de vectores que pode criar. E finalmente, a base diz-lhe o menor conjunto de vectores necessários para abranger um espaço vectorial, e assim a estrutura desse espaço.

Masterizar estes conceitos dar-lhe-á a base necessária para uma compreensão concreta da álgebra linear. Afinal, uma casa não pode ficar sobre uma base instável, e nós não podemos compreender a álgebra linear sem uma base. Obrigado pela sua leitura!