Departamento de Informática e Tecnologia
O que é uma máquina Turing?
Uma máquina Turing é uma máquina hipotética pensada pelo matemático Alan Turing em 1936. Apesar da sua simplicidade, a máquina pode simular QUALQUER algoritmo de computador, por mais complicado que seja!

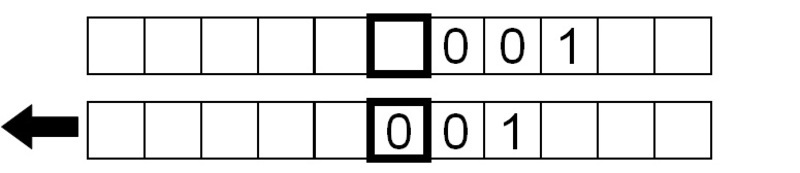
Acima é uma representação muito simples de uma máquina Turing. Consiste numa fita infinitamente longa que actua como a memória num computador típico, ou qualquer outra forma de armazenamento de dados. Os quadrados da fita estão normalmente em branco no início e podem ser escritos com símbolos. Neste caso, a máquina só pode processar os símbolos 0 e 1 e ” ” (em branco), e assim se diz ser uma máquina Turing de 3 símbolos.
De cada vez, a máquina tem uma cabeça que é posicionada sobre um dos quadrados da fita. Com esta cabeça, a máquina pode efectuar três operações muito básicas:
- Leia o símbolo no quadrado debaixo da cabeça.
- Editar o símbolo escrevendo um novo símbolo ou apagando-o.
- Mover a fita à esquerda da direita por um quadrado de modo a que a máquina possa ler e editar o símbolo num quadrado vizinho.
Uma demonstração simples
Como um exemplo trivial para demonstrar estas operações, vamos tentar imprimir os símbolos “1 1 0” numa fita inicialmente em branco:

P>Primeiro, escrevemos um 1 no quadrado debaixo da cabeça:

Próximo, movemos a fita adesiva deixada por um quadrado:

Agora, escreva 1 no novo quadrado debaixo da cabeça:

P>Pomos novamente a fita adesiva esquerda por um quadrado:
Finalmente, escreve um 0 e já está!

Um programa simples
Com os símbolos “1 1 0” impressos na fita, vamos tentar converter o 1s para 0s e vice-versa. A isto chama-se inversão de bits, visto que 1s e 0s são bits em binário. Isto pode ser feito passando as seguintes instruções à máquina Turing, utilizando as capacidades de leitura da máquina para decidir as suas operações subsequentes por si só. Estas instruções constituem um programa simples.
| Symbol read | Write instruction | Move instruction |
|---|---|---|
| Blank | None | None |
| 0 | Write 1 | Move tape à direita |
| 1 | Escrever 0 | Move tape à direita |
A máquina lerá primeiro o símbolo debaixo da cabeça, escrever um novo símbolo em conformidade, depois mover a fita à esquerda ou à direita conforme as instruções, antes de repetir novamente a sequência de leitura-escrita-movimento.
Vejamos o que este programa faz à nossa fita a partir do ponto final anterior das instruções:

O símbolo actual debaixo da cabeça é 0, por isso escrevemos um 1 e movemos a fita para a direita por um quadrado.
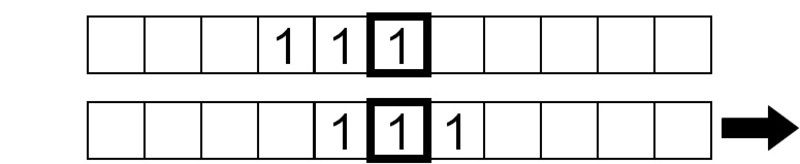
O símbolo lido é agora 1, por isso escrevemos um 0 e movemos a fita à direita por um quadrado:
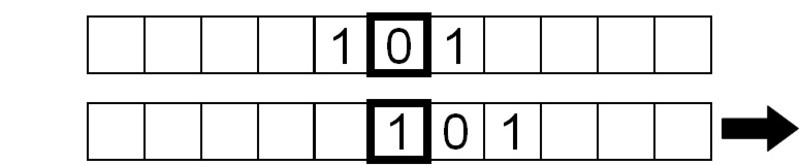
Simplesmente, o símbolo lido é um 1, por isso repetimos as mesmas instruções.
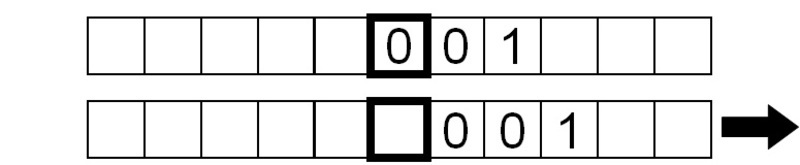
Finalmente, um símbolo ‘em branco’ é lido, pelo que a máquina não faz nada além de ler o símbolo em branco continuamente, uma vez que lhe instruímos para repetir a sequência de leitura-escrita-escrita sem parar.
De facto, o programa está incompleto. Como é que a máquina repete a sequência infinitamente, e como é que a máquina pára de executar o programa? O programa diz-lhe para com o conceito de estado da máquina.
O estado da máquina
Para completar o programa, o estado muda durante a execução do programa na máquina. As seguintes alterações, marcadas em itálico, devem ser aditadas à nossa tabela, que agora pode ser chamada de tabela de estados:
| State | Symbol read | Write instruction | Move instruction | Next state |
|---|---|---|---|---|
| State 0 | Blank | None | None | Stop state |
| >/td> | 0 | Escrever 1 | Mover a fita à direita | Estado 0 |
| /td> | 1 | Escrever 0 | Mover a fita à direita | State 0 |
Alocamos o conjunto anterior de instruções a um estado de máquina, para que a máquina execute essas instruções quando se encontra no estado especificado.
Após cada instrução, especificamos também um estado para o qual a máquina transitará. No exemplo, a máquina é redireccionada de volta ao seu estado original, Estado 0, para repetir a sequência de leitura-escrita-nove, a menos que seja lido um símbolo em branco. Quando a máquina lê um símbolo em branco, a máquina é direccionada para um estado de paragem e o programa termina.
Máquinas de estado finito
P>Even, embora pareça tolice fazê-lo, vamos agora adicionar um estado adicional ao nosso programa que reverte os bits já invertidos “1 1 0” de “0 0 1” para “1 1 0”. Abaixo está a tabela actualizada, com as alterações listadas em itálico. A máquina Turing age agora como uma máquina de estado finito com dois estados – estes são chamados de máquinas Turing de três símbolos, de dois estados.
| State | Symbol read | Write instrução | Next state | |
|---|---|---|---|---|
| State 0 | Blank | Write em branco | ||
| Mover a fita à direita | State 1 | |||
| /td>>>1 | Escrever 0 | Mover o fita à direita | State 0 | |
| State 1 | Blank | Escrever em branco | Mover a fita à direita | Stop state |
| /td> | 0 | Escrever 1 | ||
Para a instrução de escrita, “Nenhum” foi alterado para “Escrever em branco” por uma questão de uniformidade (para que apenas os símbolos da máquina sejam referidos), e deve ser notado que são equivalentes.
Em vez de uma tabela de estados, o programa também pode ser representado com um diagrama de estados:
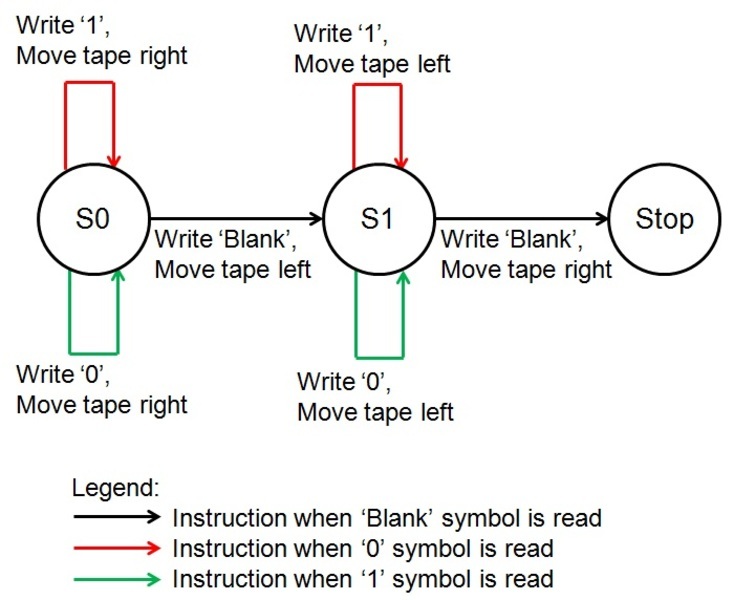
De onde o programa estava anteriormente, em vez de não fazer nada e parar depois de a máquina encontrar um símbolo em branco, instruímo-lo a mover a fita à esquerda antes de transitar para o estado 1, onde inverte o processo de inversão de bits.
Next, voltamos a inverter os bits, desta vez movendo a fita para a esquerda em vez da direita.
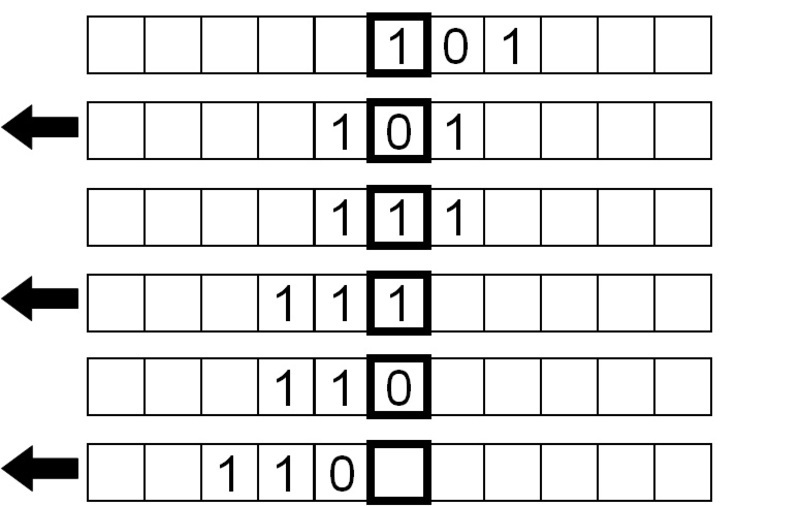
Finalmente, é lido um símbolo em branco, por isso movemos a fita para a direita para voltarmos ao ponto de partida, e paramos o programa.

Com a introdução de mais estados no nosso programa, podemos instruir a máquina Turing para executar funções mais complexas e, assim, executar qualquer algoritmo que um computador moderno possa.
Na secção dois, vamos aprender sobre LEDs, pinos GPIO, resistências, e píton, antes de embarcarmos na construção da nossa máquina Turing!