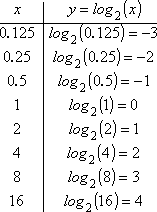Funções Logarítmicas Gráficas: Introdução

p>Voltar ao Índice de Lições | Fazer as Lições por Ordem | Página de fácil impressão
p> Funções Logarítmicas Gráficas: Introdução (página 1 de 3)

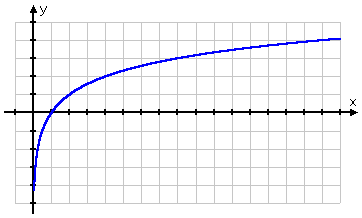
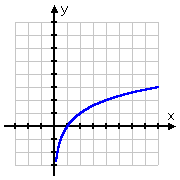
Pela natureza do logaritmo, a maioria dos gráficos de log tendem a ter a mesma forma, parecendo semelhante a um gráfico de raiz quadrada:

y = sqrt(x)	y = log2(x)

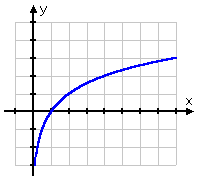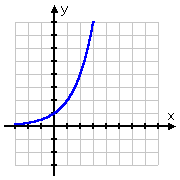
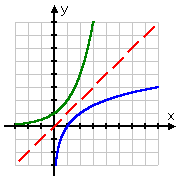
O gráfico da raiz quadrada começa no ponto (0, 0) e depois sai para a direita. Por outro lado, o gráfico do tronco passa (1, 0), saindo para a direita mas também deslizando para o lado positivo do eixo y. Recordando que os toros são os inversos dos exponenciais, esta forma para o gráfico do toro faz todo o sentido: o gráfico do toro, sendo o inverso do exponencial, seria apenas o “flip” do gráfico do exponencial:

y = 2x	y = log2(x)
comparação dos dois gráficos, mostrando a linha de inversão em vermelho

É bastante simples fazer gráficos exponenciais. Por exemplo, para fazer o gráfico y = 2x, basta ligar alguns valores para x, calcular os valores y correspondentes, e traçar os pontos. Mas como se fazem os gráficos dos exponenciais? Há duas opções. Aqui está a primeira: Copyright © Elizabeth Stapel 2002-2011 Todos os direitos reservados

• Gráfico y = log2(x).

Para fazer o gráfico “à mão”, preciso primeiro de lembrar que os registos não são definidos para x negativo ou para x = 0. Devido a esta restrição no domínio (os valores de entrada) do log, nem me vou dar ao trabalho de tentar encontrar valores y para, digamos, x = -3 ou x = 0. Em vez disso, vou começar com x = 1, e trabalhar a partir daí, utilizando a definição do log.

Desde 20 = 1, então log2(1) = 0, e (1, 0) está no gráfico.
Desde 21 = 2, depois log2(2) = 1, e (2, 1) está no gráfico.
Uma vez que 3 não é uma potência de 2, então log2(3) será um valor confuso. Portanto, não me incomodarei com o gráfico x = 3.
Desde 22 = 4, depois log2(4) = 2, e (4, 2) está no gráfico.
Já que 5, 6, e 7 também não são potências de 2, vou saltá-los e passar para x = 8.
Desde 23 = 8, depois log2(8) = 3, por isso (8, 3) está no gráfico.
A potência seguinte de 2 é 16: desde 24 = 16, depois log2(16) = 4, e (16, 4) está no gráfico.
A potência seguinte de 2, x = 32, é demasiado grande para o meu gosto; não me apetece desenhar o meu gráfico assim tão largo, por isso vou desistir com x = 16.

O acima dá-me o ponto (1, 0) e alguns pontos à direita, mas o que faço para valores x entre 0 e 1? Para este intervalo, preciso de pensar em termos de poderes negativos e recíprocos. Tal como a “metade” da função exponencial à esquerda tinha poucos pontos grafáveis (o resto deles estando demasiado próximo do eixo x), assim também a “metade” inferior da função log tem poucos pontos grafáveis, o resto deles estando demasiado próximo do eixo y. Mas posso encontrar alguns:

Desde 2-1 = 1/2 = 0,5, depois log2(0,5) = -1, e (0,5, -1) está no gráfico.

Desde 2-2 = 1/4 = 0,25, depois log2(0,25) = -2, e (0,25, -2) está no gráfico.

Desde 2-3 = 1/8 = 0,125, depois log2(0.125) = -3, e (0,125, -3) está no gráfico.

A potência seguinte de 2 (enquanto x se move nesta direcção) é 1/16 = 2-4, mas o valor x para o ponto (0,0625, -4) parece demasiado pequeno para se preocupar, por isso vou desistir com os pontos que já encontrei.

Listar estes pontos dá-me o meu gráfico T:
Desenhar os meus pontos e depois esboçar na linha (lembrando-se de não ir para a esquerda do eixo y!), recebo este gráfico:

Top | 1 | 2 | 3 | Return to Index Next >>