Oval
Um oval é uma curva que se assemelha a um círculo esmagado mas, ao contrário da elipse, sem uma definição matemática precisa. A palavra oval derivada da palavra latina “ovus” para ovo. Ao contrário das elipses, as ovais têm por vezes apenas um único eixo de simetria de reflexão (em vez de dois).
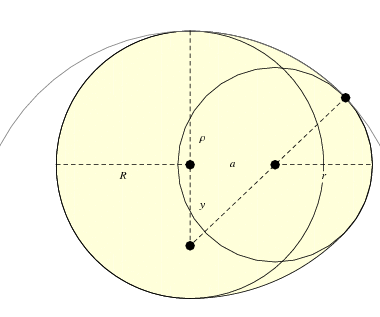 p> A variante particular ilustrada acima pode ser construída com uma bússola juntando arcos de raios diferentes, de modo a que os centros dos arcos fiquem numa linha que passa pelo ponto de junção (Dixon 1991). Albrecht Dürer utilizou este método para desenhar uma fonte de letra romana. Se a separação entre as maiúsculas esquerda e direita for
p> A variante particular ilustrada acima pode ser construída com uma bússola juntando arcos de raios diferentes, de modo a que os centros dos arcos fiquem numa linha que passa pelo ponto de junção (Dixon 1991). Albrecht Dürer utilizou este método para desenhar uma fonte de letra romana. Se a separação entre as maiúsculas esquerda e direita for ![]() e os raios forem
e os raios forem ![]() e
e ![]() , respectivamente, com
, respectivamente, com ![]() e
e ![]() , depois o centro
, depois o centro ![]() e raio
e raio ![]() do círculo de união são
do círculo de união são
|
(1)
|
|||
|
(2)
|
Chamar os três círculos ![]()
![]() , e
, e ![]() . Que o ponto superior de intersecção de
. Que o ponto superior de intersecção de ![]() e
e ![]() seja
seja ![]() , deixe o ângulo entre a linha tracejada vertical e a linha através de
, deixe o ângulo entre a linha tracejada vertical e a linha através de ![]() be
be ![]() , e deixar o ângulo entre o raio horizontal de
, e deixar o ângulo entre o raio horizontal de ![]() e linha tracejada através de
e linha tracejada através de ![]() be
be ![]() . Then
. Then
|
(3)
|
|||
|
(4)
|
|||
|
(5)
|
|||
|
(6)
|
e metade da área delimitada pela oval é a soma das áreas do quarto de círculo mais à esquerda, o sector de ![]() , e o sector de
, e o sector de ![]() menos a área da porção triangular do sector de
menos a área da porção triangular do sector de ![]() deitado abaixo do
deitado abaixo do ![]() -eixo, so
-eixo, so
|
(7)
|
|||
|
(8)
|
|||
![1/2(a^2-3r^2+2rR+R^2))/(2(R-r)^2)tan^(-1)((2a(R-r))/(a^2-(R-r)^2))].](https://mathworld.wolfram.com/images/equations/Oval/Inline49.gif) |
(9)
|
Como esperado, esta fórmula reduz à área de um círculo
|
(10)
|
for ![]() , e para a área de um estádio
, e para a área de um estádio
|
(11)
|
para ![]() .
.