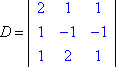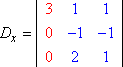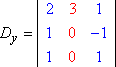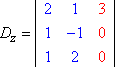Regra de Cramer

p>Volta ao Índice de Lições | Fazer as Lições por Ordem | Página de fácil impressão
p> Regra de Cramer

Dado um sistema de equações lineares, A Regra de Cramer é uma forma útil de resolver apenas uma das variáveis sem ter de resolver todo o sistema de equações. Normalmente não ensinam a Regra de Cramer desta forma, mas este é suposto ser o objectivo da Regra: em vez de resolver todo o sistema de equações, pode-se usar Cramer’s para resolver apenas uma única variável.

Vamos utilizar o seguinte sistema de equações:

2x + y + z = 3
x – y – z = 0
x + 2y + z = 0

Temos o lado esquerdo do sistema com as variáveis (a “matriz de coeficiente”) e o lado direito com os valores de resposta. Que D seja o determinante da matriz de coeficiente do sistema acima, e que Dx seja o determinante formado pela substituição dos valores da coluna x pelos valores da coluna de resposta:

Similiarmente, Dy e Dz seriam então: Copyright © Elizabeth Stapel 2004-2011 Todos os direitos reservados

Avaliar cada determinante (utilizando o método aqui explicado), obtemos:

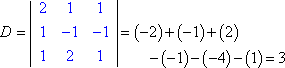
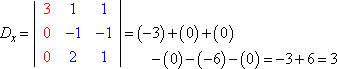
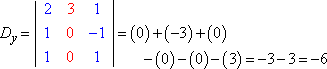
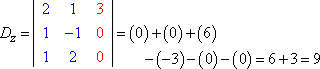
Regra do Cramer diz que x = Dx ÷ D, y = Dy ÷ D, e z = Dz ÷ D. Isto é:

x = 3/3 = 1, y = -6/3 = -2, e z = 9/3 = 3

É tudo o que há para a Regra de Cramer. Para encontrar a variável que quiser (chame-lhe “ß” ou “beta”), basta avaliar o quociente determinante Dß ÷ D. (Por favor, não me peça para explicar porque é que isto funciona. Apenas confie em mim que os determinantes podem funcionar em muitos tipos de magia.)

• Dado o seguinte sistema de equações, encontre o valor de z.

2x + y + z = 1
x – y + 4z = 0
x + 2y – 2z = 3

Para resolver apenas para z, primeiro encontro o determinante do coeficiente.

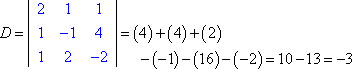
Então, eu formo Dz substituindo a terceira coluna de valores pela coluna de respostas:

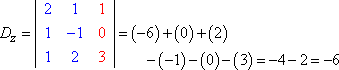
Então eu formo o quociente e simplifico:

z = 2

O objectivo da Regra de Cramer é que não tem de resolver todo o sistema para obter o valor único de que necessita. Isto poupou-me bastante tempo em alguns testes de física. Esqueci-me no que estávamos a trabalhar (algo com fios e correntes, penso eu), mas a Regra de Cramer foi muito mais rápida do que qualquer outro método de solução (e Deus sabe que eu precisava do tempo extra). Não se deixe confundir por todas as subscrições e coisas; a Regra é realmente muito simples. Basta escolher a variável que pretende resolver, substituir a coluna de valores dessa variável no coeficiente determinante pelos valores da coluna de respostas, avaliar esse determinante, e dividir pelo coeficiente determinante. É só isso.

Almost.

E se o determinante do coeficiente for zero? Não se pode dividir por zero, então o que é que isto significa? Não posso entrar nos aspectos técnicos aqui, mas “D = 0” significa que o sistema de equações não tem uma solução única. O sistema pode ser inconsistente (nenhuma solução) ou dependente (uma solução infinita, que pode ser expressa como uma solução paramétrica tal como “(a, a + 3, a – 4)”). Em termos da Regra de Cramer, “D = 0” significa que terá de usar algum outro método (tal como operações em fila de matriz) para resolver o sistema. Se D = 0, não poderá utilizar a Regra de Cramer.

Top | Voltar ao Índice