SAT / ACT Prep Online Guides and Tips

Se estiver a estudar trigonometria ou cálculo – ou a preparar-se para – terá de se familiarizar com o círculo de unidade. O círculo unitário é uma ferramenta essencial utilizada para resolver para o seno, cosseno, e tangente de um ângulo. Mas como é que funciona? E que informação precisa de saber para a utilizar?

Neste artigo, explicamos o que é o círculo unitário e porque o deve conhecer. Também lhe damos três dicas para o ajudar a lembrar como utilizar o círculo unitário.

Imagem da unidade: Gustavb/Wikimedia

O Círculo unitário: Uma Introdução Básica

O círculo unitário é um círculo com um raio de 1. Isto significa que para qualquer recta traçada desde o ponto central do círculo até qualquer ponto ao longo da margem do círculo, o comprimento dessa recta será sempre igual a 1. (Isto também significa que o diâmetro do círculo será igual a 2, uma vez que o diâmetro é igual ao dobro do comprimento do raio.)

Tipicamente, o ponto central da circunferência unitária é onde os eixos x e y se intersectam, ou nas coordenadas (0, 0):

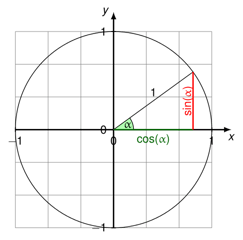
O círculo unitário, ou círculo trigêmeo como também é conhecido, é útil de saber porque nos permite calcular facilmente o cosseno, seno, e tangente de qualquer ângulo entre 0° e 360° (ou 0 e 2π radianos).

Como se pode ver no diagrama acima, desenhando um raio em qualquer ângulo (marcado por ∝ na imagem), estará a criar um triângulo direito. Neste triângulo, o co-seno é a linha horizontal, e o seno é a linha vertical. Por outras palavras, cosseno = x-coordenado, e seno = y-coordenado. (A linha mais longa do triângulo, ou hipotenusa, é o raio e, portanto, igual a 1.)

Porquê tudo isto é importante? Lembre-se que pode resolver para os comprimentos dos lados de um triângulo usando o teorema de Pitágoras, ou $a^2+b^2=c^2$ (em que a e b são os comprimentos dos lados do triângulo, e c é o comprimento da hipotenusa).

Sabemos que o co-seno de um ângulo é igual ao comprimento da linha horizontal, o seno é igual ao comprimento da linha vertical, e a hipotenusa é igual a 1. Portanto, podemos dizer que a fórmula para qualquer triângulo direito no círculo unitário é a seguinte:

$$\cos^2θ+\sin^2θ=1^2$

Desde $1^2=1$, podemos simplificar esta equação desta forma:

$$\cos^2θ+\sin^2θ=1$$

Cuidado que estes valores podem ser negativos dependendo do ângulo formado e em que quadrante caem as coordenadas x e y (explicarei isto com mais detalhe mais tarde).

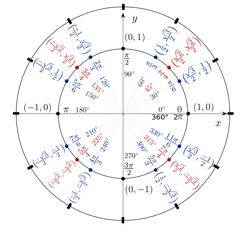
Aqui está uma visão geral de todos os ângulos principais em graus e radianos no círculo da unidade:

h3>Círculo Unitário – Graus

Círculo Unitário – Graus

Mas e se não houver um triângulo formado? Vejamos o que acontece quando o ângulo é 0°, criando uma linha recta horizontal ao longo do eixo x:

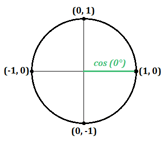
Nesta linha, a coordenada x é igual a 1 e a coordenada y é igual a 0. Sabemos que o co-seno é igual à coordenada x, e o seno é igual à coordenada y, por isso podemos escrever isto:

• $\cos0°=1$
• $\sin0°=0$

E se o ângulo for 90° e fizer uma linha perfeitamente vertical ao longo do eixo y?

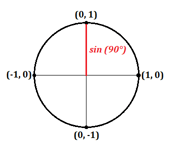
Aqui, podemos ver que a coordenada x é igual a 0 e a coordenada y é igual a 1. Isto dá-nos os seguintes valores para seno e coseno:

• $\cos90°=0$
• $\sin90°=1$

Este slogan aplica-se definitivamente se não for um amante de matemática.

h2>Porque Deve Conhecer o Círculo de Unidade

Como foi dito acima, o círculo de unidade é útil porque nos permite resolver facilmente para o seno, cosseno, ou tangente de qualquer grau ou radiano. É especialmente útil conhecer a tabela de unidades de círculo se precisar de resolver para certos valores de trigonometria para trabalhos de casa de matemática ou se estiver a preparar-se para estudar cálculo.

Mas como é que saber exactamente o círculo unitário o pode ajudar? Digamos que lhe é dado o seguinte problema num teste de matemática – e não lhe é permitido usar uma calculadora para o resolver:

$\sin30°$

Por onde começa? Vamos dar novamente uma vista de olhos à tabela de unidades circulares – este tempo com todos os ângulos principais (em graus e radianos) e as suas coordenadas correspondentes:

Jim.belk/Wikimedia

Não fique sobrecarregado! Lembre-se, tudo pelo que está a resolver é $\sin30°$. Ao olhar para este gráfico, podemos ver que a coordenada y é igual a $1/2$ a 30°. E uma vez que a coordenada y é igual a seno, a nossa resposta é a seguinte:

$$\sin30°=1/2$

Mas e se tiver um problema que usa radianos em vez de graus? O processo para o resolver continua a ser o mesmo. Digamos, por exemplo, que se obtém um problema com este aspecto:

$$\cos{{3π}/4}$$

p>Again, utilizando o gráfico acima, podemos ver que a x-coordenada (ou coseno) por ${3π}/4$ (que é igual a 135°) é $-{√2}/2$. Eis como seria a nossa resposta a este problema então:

$$\cos({3π}/4)=-{√2}/2$$

Tudo isto é bastante fácil se tiver a tabela de unidades circulares acima para usar como referência. Mas a maioria (se não todas) das vezes, este não será o caso, e espera-se que responda a este tipo de perguntas de matemática usando apenas o seu cérebro.

Então como se pode lembrar do círculo unitário? Continue a ler para as nossas dicas de topo!

Como recordar o círculo unitário: 3 dicas essenciais

Nesta secção, damos-lhe as nossas dicas de topo para recordar o círculo de trigonometria para que possa usá-lo com facilidade para qualquer problema matemático que o requeira.

Não recomendaria praticar o círculo unitário com post-its, mas, ei, é um começo.

#1: Memorizar ângulos e coordenadas comuns

Para utilizar o círculo unitário eficazmente, será necessário memorizar os ângulos mais comuns (tanto em graus como em radianos), bem como as suas correspondentes coordenadas x e y.

O diagrama acima é uma tabela de círculos unitários útil para observar, uma vez que inclui todos os ângulos principais em graus e radianos, além dos seus correspondentes pontos de coordenadas ao longo dos eixos x e y.

Aqui está uma tabela que lista esta mesma informação em forma de tabela:

>>div>$π/3$

>>div>$π/2$>>div>(0, 1)

>>>div>120°>>>div>${2π}/3$>>>div>$(-1/2 {√3}/2)$

>>div>π>/td>>>>div>(-1, 0)

>>>div>210°>>div>${7}/6$

>>div>>225°>>div>${5π}/4$

div>Angle (Degrees)	Angle (Radians)	Coordenadas do Ponto no Círculo
0 / 2π	(1, 0)
>div>$({√3}/2, 1/2)$
>>div>$π/4$	>div>$({√2}/2, {√2}/2)$
60°	$(1/2,{√3}/2)$
90°
135°	${3π}/4$	$(-{√2}/2, {√2}/2)$
150°	${5π}/6$	$(-{√3}/2, 1/2)$
>div>$(-{√3}/2, -1/2)$
$(-{√2}/2, -{√2}/2)$
240°	${4π}/3$	$(-1/2, -{√3}/2)$
270°	${3π}/2$	(0, -1)
300°	$(1/2, -{√3}/2)$
315°	${7π}/4$	$({√2}/2, -{√2}/2)$
${11π}/6$	$({√3}/2, -1/2)$

Agora, embora seja mais do que bem-vindo para tentar memorizar todas estas coordenadas e ângulos, isto é muita coisa para recordar.

Felizmente, há um truque que pode usar para o ajudar a lembrar-se das partes mais importantes do círculo da unidade.

Leve as coordenadas acima e notará um padrão claro: todos os pontos (excluindo aqueles a 0°, 90°, 270°, e 360°) alternam entre apenas três valores (sejam positivos ou negativos):

• $1/2$
• ${√2}/2$
• ${√3}/2$

Cada valor corresponde a uma linha curta, média ou longa tanto para o co-seno como para o seno:

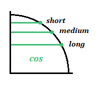
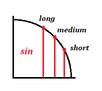
Aqui está o significado destes comprimentos:

• linha horizontal ou vertical curta = $1/2$
• linha horizontal ou vertical média = ${√2}/2$
• linha horizontal ou vertical longa = ${√3}/2$

Por exemplo, se estiver a tentar resolver $\cos{π/3}$, deve saber imediatamente que este ângulo (que é igual a 60°) indica uma linha horizontal curta no círculo da unidade. Portanto, a sua coordenada x correspondente deve ser igual a $1/2$ (um valor positivo, já que $π/3$ cria um ponto no primeiro quadrante do sistema de coordenadas).

Finalmente, embora seja útil memorizar todos os ângulos na tabela acima, note-se que de longe os ângulos mais importantes a lembrar são os seguintes:

• 30° / $π/6$
• 45° / $π/4$
• 60° / $π/3$

Trate os seus negativos e positivos como trataria os cabos que podem potencialmente matá-lo se engatasse incorrectamente.

#2: Aprenda o que é Negativo e o que é Positivo

É crítico ser capaz de distinguir as coordenadas x- e y positivas e negativas para que se encontre o valor correcto para um problema de trigonometria. Como lembrete, se uma coordenada no círculo unitário será positiva ou negativa depende do quadrante (I, II, III, ou IV) em que o ponto se enquadra:

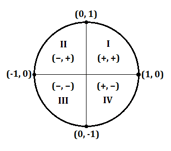
Aqui está um gráfico que mostra se uma coordenada será positiva ou negativa com base no quadrante em que se encontra um determinado ângulo (em graus ou radianos):

>div>+

>div>IV/td>

div>Quadrant	X-Coordinate (Cosine)	Y-Coordinate (Sine)
I	>div>+/td>>>/td>
–	+
>div>III	–	–
+	–

Por exemplo, dizem que lhe é dado o seguinte problema num teste de matemática:

$\cos210°$

Antes mesmo de tentar resolvê-lo, deverá ser capaz de reconhecer que a resposta será um número negativo uma vez que o ângulo 210° cai no quadrante III (onde as x-coordenadas são sempre negativas).

Agora, usando o truque que aprendemos na dica 1, pode descobrir que um ângulo de 210° cria uma longa linha horizontal. Portanto, a nossa resposta é a seguinte:

$$\cos210°=-{√3}/2$$

#3: Know How to Solve for Tangent

Por último, é essencial saber como utilizar toda esta informação sobre o círculo trigêmeo e seno e cosseno para poder resolver para a tangente de um ângulo.

Em trigonometria, para encontrar a tangente de um ângulo θ (em graus ou radianos), basta dividir o seno pelo co-seno:

$\tanθ={\sinθ}/{\cosθ}$

Por exemplo, digamos que se está a tentar responder a este problema:

$$300°$$

O primeiro passo é estabelecer uma equação em termos de seno e coseno:

$$300°={\sin300°}/{\cos300°}$$

Agora, para resolver para a tangente, precisamos de encontrar o seno e o coseno de 300°. Deve ser possível reconhecer rapidamente que o ângulo de 300° cai no quarto quadrante, o que significa que o cosseno, ou x-coordenado, será positivo, e o seno, ou y-coordenado, será negativo.

É preciso saber de imediato que o ângulo 300° cria uma linha horizontal curta e uma linha vertical longa. Portanto, o co-seno (a linha horizontal) será igual a $1/2$, e o seno (a linha vertical) será igual a $-{√3}/2$ (um valor y negativo, já que este ponto está no quadrante IV).

Agora, para encontrar a tangente, tudo o que se faz é ligar e resolver:

$$\tan300°={-{√3}/2}/{1/2}$$

$$\tan300°=-√3$$

Time de ronronar as suas capacidades matemáticas!

Unit Circle Practice Question Set

Agora que sabe como é o círculo da unidade e como usá-lo, vamos testar o que aprendeu com alguns problemas de prática.

Questões

1. $\sin45°$
2. $\cos240°$
3. $\cos{5π}/3$
4. $\tan{2π}/3$

Respostas

1. ${√2}/2$
2. $-1/2$
3. $1/2$
4. $-√3$

Explicações das respostas

#1: $\sin45°$

Com este problema, há duas informações que deve ser capaz de identificar de imediato:

A resposta será positiva, uma vez que o ângulo 45° está no quadrante I, e o seno de um ângulo é igual ao da coordenada y

• O ângulo 45° cria uma linha vertical de comprimento médio (para seno)

Desde que 45° indica uma linha positiva de comprimento médio, a resposta correcta é ${√2}/2$.

Se não tiver a certeza de como descobrir isto, desenhe um diagrama para o ajudar a determinar se o comprimento da linha será curto, médio, ou longo.

#2: $\cos240°$

Problema #1 acima, há duas informações que deve ser capaz de compreender rapidamente com este problema:

A resposta será negativa, uma vez que o ângulo 240° está no quadrante III, e o cosseno de um ângulo é igual à coordenada x

• O ângulo 240° cria uma linha horizontal curta (para cosseno)

Desde que 240° indica uma linha negativa, curta, a resposta correcta é $-1/2$.

##3: $\cos{5π}/3$

Não parecido com os problemas acima, este problema utiliza radianos em vez de graus. Embora isto possa fazer o problema parecer mais complicado de resolver, na realidade usa os mesmos passos básicos que os outros dois problemas.

P>Primeiro, deve-se reconhecer que o ângulo ${5π}/3$ está no quadrante IV, pelo que a coordenada x, ou cosseno, será um número positivo. Também deve ser capaz de dizer que ${5π}/3$ cria uma linha horizontal curta.

Isto dá-lhe informação suficiente para determinar que a resposta é $1/2$.

#4: $\tan{2π}/3$

Este problema lida com tangente em vez de seno ou cosseno, o que significa que exigirá um pouco mais de matemática do nosso lado. Em primeiro lugar, recordar a fórmula básica para encontrar a tangente:

$$\tan θ={\sin θ}/{\cos θ}$

Agora, vamos pegar no grau que nos foi dado -${2π}/3$-e ligá-lo a esta equação:

$$\tan {2π}/3={\sin {2π}/3}/{\cos {2π}/3}$$

Deverá agora ser capaz de resolver para o seno e o cosseno separadamente usando o que memorizou sobre o círculo da unidade. Como o ângulo ${2π}/3$ está no quadrante II, a coordenada x (ou cosseno) será negativa, e a coordenada y (ou seno) será positiva.

Nextra, deverá ser capaz de determinar com base apenas no ângulo que a linha horizontal é uma linha curta, e a linha vertical é uma linha longa. Isto significa que o co-seno é igual a $-1/2$, e o seno é igual a ${√3}/2$.

Agora que descobrimos estes valores, tudo o que temos de fazer é ligá-los à nossa equação inicial e resolver para a tangente:

$$\tan {2π}/3={{√3}/2}/{-1/2}$

$\tan {2π}/3=-√3$

O que se segue?

Se estiver a fazer o SAT ou ACT em breve, precisará de conhecer alguma trigonometria para se poder sair-se bem na secção de matemática. Dê uma vista de olhos aos nossos guias especializados de trigonometria no SAT e ACT para que possa aprender exactamente o que precisa de saber para o dia do teste!

Besides memorizando o círculo de unidades, é uma boa ideia aprender como ligar os números e como ligar as respostas. Leia os nossos guias para aprender tudo sobre estas duas estratégias úteis, que pode utilizar em qualquer teste de matemática – incluindo o SAT e o ACT!

Tem amigos que também necessitem de ajuda com a preparação para o teste? Partilhe este artigo!