Solução de Problemas do Mundo Real

Uma Lição para a Primeira e Segunda Classe

Uma lição para os alunos do primeiro ano

por Chris Confer

Quando as crianças utilizam a matemática para resolver problemas do mundo real, aprendem que a matemática não é apenas algo a fazer para o bem do professor, mas oferece-lhes ferramentas importantes para moldar o seu mundo. Nesta lição, que aparece no novo livro de Chris Confer, Teaching Number Sense, Grade 1 (Math Solutions Publications, 2005), pede-se às crianças que descubram quantos biscoitos precisam para um tratamento de classe.

“Amanhã é o Dia das Crianças”, disse eu, “e poderíamos celebrar tendo biscoitos. Teria todo o gosto em trazer dois bolinhos para cada um de vós, mas gostaria de saber quantos bolinhos levar. O que precisamos de saber para perceber isto?”

“Quantas bolachas?” Juanita perguntou.

“Sim, é isso que precisamos de saber muitos cookies que precisamos para que cada um de vós possa ter dois. Quantas crianças há na nossa turma?” continuei. As crianças concordaram que eram vinte e duas. Escrevi: “Há 22 crianças no quadro. Depois acrescentei: “Se cada criança receber 2 bolachas, de quantas bolachas precisamos?

“Podem fazer desenhos ou usar cubos ou qualquer outra coisa para o descobrir”, disse eu. “Podes trabalhar sozinho ou com um parceiro ou parceiros”

Again I asked, “Quantas crianças estão nesta sala? As crianças responderam, “Vinte e dois”

“E de quantos biscoitos precisa cada um?” “Dois biscoitos”, disseram eles.

“Quero que cada um de vocês mostre a sua resposta e como a descobriram num pedaço de papel”, continuei. “Use palavras, números e figuras para mostrar o que fez”

Alfredo começou a desenhar figuras de pau e dois biscoitos ao lado de cada um, mas depois de duas figuras de pau, abandonou esta ideia. “É demasiado difícil”, disse-me ele. “Posso começar de novo?” Ele virou o seu papel e começou a desenhar conjuntos de duas bolachas. Cada par de bolachas tinha um espaço ligeiramente maior entre ele e o par seguinte.

Alejandrina, Navin, e Alicia tinham desenhado pares de bolachas e tinham circulado os pares. Estavam a contar para verificar se tinham vinte e dois pares. Navin tinha escrito 2 1 2 1 2 1 2 . . . e estava a contar por uns. “Quarenta e quatro”, disse ele triunfantemente.

Lorena fez pontos para os seus biscoitos. Os pares de biscoitos foram claramente separados um do outro. Ela contou-os, desenhou mais alguns, e recontou-os de um para verificar quantos biscoitos tinha.

Fui para Sereslinda, que tinha feito círculos para os biscoitos, todos em linha, sem qualquer espaço que separasse os pares de biscoitos. Ela parou para contar os biscoitos e chegou aos dezasseis. Perguntava-me o que faria a seguir.

Alfredo tinha decidido fazer círculos para os seus pares de biscoitos. “Estes vão juntos”, disse ele. “São duas crianças”. Parecia que Alfredo tinha começado a confundir o que os círculos representavam: eram biscoitos ou crianças? Decidi não intervir e ver se ele próprio conseguiria resolver isto. (Ver Figura 1.)

p>Figure 1. Apesar de ter circulado pares,
O papel de Alfredo mostrou vinte e dois biscoitos, em vez de
vinte e dois pares de biscoitos.

Sereslinda também tinha começado a circular pares de biscoitos, talvez para mostrar que cada criança recebeu dois biscoitos. Ela parou periodicamente para contar os pares de biscoitos. Quando tinha vinte e dois, ela parou.

Sereslinda começou então a desenhar pessoas de pau. Ela fez dez e depois começou a escrever números para se repudiar – ressentir das outras crianças da turma. Os seus números subiram para vinte e dois, mas ela só tinha desenhado apenas onze figuras de pau e dez números. Sereslinda tinha contado mal, mas eu estava interessado em como ela tinha passado para uma forma mais eficiente de representar: usando números em vez de desenhos.

Algardei quando Sereslinda começou a verificar se tinha pares de bolachas suficientes para cada criança da turma. Ela traçou linhas para ligar cada pessoa com um par de biscoitos ou cada número com um par de biscoitos. Mas isto tornou-se uma estratégia de representação pesada. (Ver Figura 2.) Sereslinda começava a parecer frustrada. Era tempo de intervir.

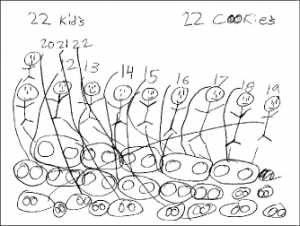p>Figure 2. Sereslinda desenhou linhas para ligar o seu pau
figurações com pares de biscoitos. As muitas linhas em
o desenho confundiu-a, e ela mudou a sua
resposta de quarenta e quatro para vinte e dois.

“Sabes o que é que eu te vejo a fazer de inteligente? perguntei a Sereslinda. “Está a corresponder para verificar se tem dois biscoitos para cada pessoa, desenhando linhas. Isso funciona bem para números mais pequenos, mas torna-se difícil com números maiores como vinte e dois. Posso dar-lhe uma sugestão?” Ela acenou com a cabeça. “Pode tentar apontar para cada par de dois biscoitos e ver se conta vinte e dois pares, tal como nós temos vinte e dois filhos”. Demonstrei-lhe isto e ela continuou a contar sozinha.

“Já chega”, disse-me ela. Fiquei satisfeito por esta estratégia alternativa ter sido útil para ela.

Lorena tinha feito vinte e dois pares de biscoitos e começou a contá-los a partir de um em inglês. Ela calculou mal em parte e de alguma forma reconheceu o seu erro. “Talvez queira contar em espanhol”, sugeri. Quando as crianças estão a fazer algo difícil, têm frequentemente mais sucesso quando usam a sua primeira língua.

Lorena começou a contar novamente em espanhol, contando a partir de dois. Ela fez isto várias vezes, certificando-se de que contava correctamente. Lorena escreveu cuidadosamente 44 cookies no topo da sua página. (Ver Figura 3.)

p>Figure 3. Lorena desenhou vinte e dois paris de biscoitos e depois contou por uns, em espanhol, a quarenta e quatro.

Voltei a Sereslinda. O seu jornal tinha vinte e dois pares de biscoitos. “Quantos biscoitos é que precisamos de ter?” perguntei eu. Sereslinda contou os grupos de dois. “Precisamos de vinte e dois biscoitos”, anunciou ela.

“Então temos vinte e duas crianças, e cada criança recebe dois biscoitos, e precisamos de trazer vinte e dois biscoitos?” perguntei eu. Sereslinda acenou com a cabeça e escreveu 22 bolachas no topo do seu jornal.

“Ela tem razão”, disse Alfredo. Mas o seu trabalho tinha uma representação muito diferente: apenas vinte e dois biscoitos em vez de vinte e dois pares de biscoitos.

Representar dois biscoitos para cada criança é difícil, uma vez que há uma quantidade de crianças que é relevante e uma quantidade de biscoitos que não corresponde ao primeiro número mas representa uma duplicação desse número. Depois de representar estas diferentes quantidades, as crianças precisam de se lembrar e interpretar qual é qual.

Após algum tempo, reuni as crianças no tapete e perguntei: “Quantas bolachas tenho de trazer se forem vinte e duas e cada uma precisa de duas bolachas? Pedi a Alfredo para partilhar primeiro.

“Há duas crianças aqui”, disse Alfredo, apontando para os dois círculos pontilhados que ele tinha desenhado para representar as bolachas. “E duas crianças aqui e duas crianças aqui”. E isso faz um, dois, três, quatro, cinco, seis, sete, oito, nove, dez, onze, doze, treze, catorze, quinze, dezasseis, dezassete, dezassete, dezoito, dezanove, vinte, vinte e um, vinte e dois. E há vinte e duas crianças e vinte e dois biscoitos”

“Por isso, pensam que se tivermos vinte e dois biscoitos, haverá o suficiente para cada um de vós ter dois biscoitos”, disse eu. Alfredo acenou com a cabeça.

“Quantos de vós concordam que precisamos de vinte e dois biscoitos?” perguntei eu. Cerca de um terço das crianças levantaram as mãos. Escrevi 22 cookies no quadro.

Pedi a Lorena para partilhar a seguir.

“Precisamos de ver todas as vinte e duas crianças e contar os cookies”, disse Lorena, apontando para os pares de cookies que ela tinha desenhado. “É um, dois, três, quatro …” Ela contou até quarenta e quatro, reconhecendo que cada par era composto por dois biscoitos.

“Não”, disse Alfredo. “São vinte e dois”

“Vamos ver o que Lorena desenhou. Onde estão as crianças?” perguntei-lhe eu. Ela apontou para cada par de bolachas, dizendo: “Isto é para mim e isto é para Sereslinda e isto é para Heriberto . . . “

“Deixou um espaço entre cada um para mostrar que o par de bolachas seguinte era para uma pessoa diferente. E depois contou todos os biscoitos?” perguntei eu. Lorena acenou com a cabeça. Contamos todos os biscoitos que Lorena tinha desenhado e chegámos aos quarenta e quatro. Escrevi 44 bolachas no quadro.

“Por isso não concordamos”, disse ao grupo. “Alguns de vós pensam que precisamos de vinte e dois biscoitos e alguns de vós pensam que são quarenta e quatro. Como podemos ter a certeza?”

“Dêem-nos os biscoitos”, algumas crianças chamaram.

“Mas eu não tenho nenhum biscoito”, disse eu. “Preciso de saber quantos devo trazer”. “Podemos usar cookies a fingir”, disse Carina.

“O que podemos usar?” perguntei eu. “Cubos”, sugeriu Heriberto.

Passamos um saco de cubos à volta do círculo, e assegurei-me de que as crianças eram frequentemente lembradas do que os cubos representavam. “Dois biscoitos para Cristina, dois biscoitos para Heriberto”. . . ” cantámos enquanto cada criança retirava dois cubos.

Pomos todos os cubos em linha, mantendo os pares de cubos juntos. Depois contamos os cubos a partir de um. Terminámos com quarenta e quatro. “Então temos vinte e dois filhos e quarenta e quatro biscoitos”, disse eu. Escrevi 44 biscoitos no quadro.

“Traz quarenta e quatro”, disse Carina.

No dia seguinte trouxe quarenta e quatro biscoitos e as crianças ficaram encantadas por cada um deles receber dois.