SAT / ACT Prep Online Guides and Tips

Wenn Sie Trigonometrie oder Analysis studieren – oder sich darauf vorbereiten – müssen Sie sich mit dem Einheitskreis vertraut machen. Der Einheitskreis ist ein wichtiges Werkzeug, um Sinus, Kosinus und Tangens eines Winkels zu bestimmen. Aber wie funktioniert er?

In diesem Artikel erklären wir Ihnen, was der Einheitskreis ist und warum Sie ihn kennen sollten. Außerdem geben wir Ihnen drei Tipps, wie Sie sich die Verwendung des Einheitskreises merken können.

Feature Image: Gustavb/Wikimedia

Der Einheitskreis: Eine grundlegende Einführung

Der Einheitskreis ist ein Kreis mit dem Radius 1. Das bedeutet, dass für jede gerade Linie, die vom Mittelpunkt des Kreises zu einem beliebigen Punkt am Rand des Kreises gezogen wird, die Länge dieser Linie immer gleich 1 ist. (Das bedeutet auch, dass der Durchmesser des Kreises gleich 2 ist, da der Durchmesser gleich der doppelten Länge des Radius ist.)

Typischerweise ist der Mittelpunkt des Einheitskreises dort, wo sich die x-Achse und die y-Achse schneiden, oder bei den Koordinaten (0, 0):

Der Einheitskreis, oder Trigonometriekreis, wie er auch genannt wird, ist nützlich zu wissen, weil wir damit leicht den Kosinus, Sinus und Tangens eines beliebigen Winkels zwischen 0° und 360° (oder 0 und 2π Bogenmaß) berechnen können.

Wie Sie im obigen Diagramm sehen können, entsteht durch das Einzeichnen eines Radius an einem beliebigen Winkel (im Bild mit ∝ markiert) ein rechtwinkliges Dreieck. In diesem Dreieck ist der Kosinus die horizontale Linie und der Sinus die vertikale Linie. Mit anderen Worten: Kosinus = x-Koordinate und Sinus = y-Koordinate. (Die längste Linie des Dreiecks, die Hypotenuse, ist der Radius und ist daher gleich 1.)

Warum ist das alles wichtig? Erinnern Sie sich daran, dass Sie die Längen der Seiten eines Dreiecks mit dem Satz des Pythagoras oder $a^2+b^2=c^2$ lösen können (wobei a und b die Längen der Seiten des Dreiecks sind und c die Länge der Hypotenuse ist).

Wir wissen, dass der Kosinus eines Winkels gleich der Länge der horizontalen Linie ist, der Sinus gleich der Länge der vertikalen Linie und die Hypotenuse gleich 1 ist. Daher können wir sagen, dass die Formel für jedes rechtwinklige Dreieck im Einheitskreis wie folgt lautet:

$$cos^2θ+\sin^2θ=1^2$

Da $1^2=1$ ist, können wir diese Gleichung wie folgt vereinfachen:

$$cos^2θ+\sin^2θ=1$

Beachten Sie, dass diese Werte negativ sein können, je nachdem, welcher Winkel gebildet wird und in welchen Quadranten die x- und y-Koordinaten fallen (das erkläre ich später noch genauer).

Hier ist eine Übersicht über alle wichtigen Winkel in Grad und Bogenmaß auf dem Einheitskreis:

Einheitskreis – Grad

Einheitskreis – Bogenmaß

Aber was ist, wenn kein Dreieck gebildet wird? Schauen wir uns an, was passiert, wenn der Winkel 0° ist und eine horizontale Gerade entlang der x-Achse entsteht:

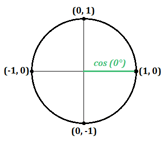
Auf dieser Linie ist die x-Koordinate gleich 1 und die y-Koordinate gleich 0. Wir wissen, dass der Kosinus gleich der x-Koordinate und der Sinus gleich der y-Koordinate ist, also können wir dies schreiben:

• $\cos0°=1$
• $\sin0°=0$

Was ist, wenn der Winkel 90° ist und eine perfekt senkrechte Linie entlang der y-Achse bildet?

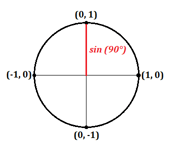
Hier können wir sehen, dass die x-Koordinate gleich 0 und die y-Koordinate gleich 1 ist. Daraus ergeben sich folgende Werte für Sinus und Cosinus:

• $\cos90°=0$
• $\sin90°=1$

Dieser Spruch trifft auf jeden Fall zu, wenn man kein Mathefanatiker ist.

Warum Sie den Einheitskreis kennen sollten

Wie bereits erwähnt, ist der Einheitskreis hilfreich, weil er es uns ermöglicht, den Sinus, Kosinus oder Tangens von jedem Grad oder Bogenmaß einfach zu lösen. Es ist besonders nützlich, die Einheitskreis-Tabelle zu kennen, wenn Sie bestimmte Trigonometrie-Werte für Mathe-Hausaufgaben lösen müssen oder wenn Sie sich auf das Studium der Infinitesimalrechnung vorbereiten.

Aber wie genau kann Ihnen die Kenntnis des Einheitskreises helfen? Nehmen wir an, Sie bekommen in einem Mathetest die folgende Aufgabe gestellt – und dürfen keinen Taschenrechner zur Lösung verwenden:

$\sin30°$

Wo fangen Sie an? Schauen wir uns noch einmal das Einheitskreisdiagramm an – diesmal mit allen Hauptwinkeln (sowohl in Grad als auch im Bogenmaß) und den dazugehörigen Koordinaten:

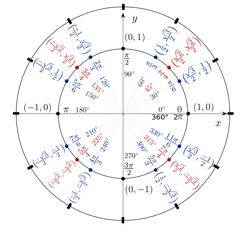Jim.belk/Wikimedia

Lassen Sie sich nicht überwältigen! Denken Sie daran, dass Sie nur $\sin30°$ lösen müssen. Anhand dieses Diagramms können wir sehen, dass die y-Koordinate gleich $1/2$ bei 30° ist. Und da die y-Koordinate gleich dem Sinus ist, lautet unsere Antwort wie folgt:

$\sin30°=1/2$

Aber was ist, wenn Sie ein Problem bekommen, das Bogenmaß statt Grad verwendet? Das Verfahren zum Lösen ist immer noch dasselbe. Nehmen wir an, Sie erhalten ein Problem, das wie folgt aussieht:

$$cos{{3π}/4}$

Auch hier können wir anhand des obigen Diagramms sehen, dass die x-Koordinate (oder der Kosinus) für ${3π}/4$ (was gleich 135° ist) $-{√2}/2$ ist. So würde unsere Antwort auf dieses Problem dann aussehen:

$$cos({3π}/4)=-{√2}/2$

Das alles ist ziemlich einfach, wenn Sie das obige Einheitskreisdiagramm als Referenz verwenden können. Aber die meiste Zeit (wenn nicht sogar die ganze) wird das nicht der Fall sein, und es wird von Ihnen erwartet, dass Sie diese Art von Mathefragen nur mit Ihrem Gehirn beantworten.

Wie können Sie sich also den Einheitskreis merken? Lesen Sie weiter für unsere Top-Tipps!

Wie man sich den Einheitskreis merkt: 3 essentielle Tipps

In diesem Abschnitt geben wir Ihnen unsere Top-Tipps, um sich den Trigonometriekreis zu merken, damit Sie ihn mit Leichtigkeit für jedes mathematische Problem verwenden können, das ihn erfordert.

Ich würde nicht empfehlen, den Einheitskreis mit Post-its zu üben, aber, hey, es ist ein Anfang.

#1: Merken Sie sich gängige Winkel und Koordinaten

Um den Einheitskreis effektiv nutzen zu können, müssen Sie sich die gängigsten Winkel (sowohl in Grad als auch im Bogenmaß) sowie die dazugehörigen x- und y-Koordinaten merken.

Das obige Diagramm ist eine hilfreiche Einheitskreis-Tabelle, da es alle wichtigen Winkel in Grad und Bogenmaß sowie die dazugehörigen Koordinatenpunkte entlang der x- und y-Achse enthält.

Hier ist ein Diagramm, das die gleichen Informationen in Tabellenform auflistet:

Winkel (Grad)	Winkel (Bogenmaß)	Koordinaten des Punktes auf dem Kreis
0° / 360°	0 / 2π	(1, 0)
30°	$π/6$	$({√3}/2, 1/2)$
	45°	$π/4$	$({√2}/2, {√2}/2)$
60°	$π/3$	$(1/2,{√3}/2)$
90°	$π/2$	(0, 1)
120°	${2π}/3$	$(-1/2, {√3}/2)$
135°	${3π}/4$	$(-{√2}/2, {√2}/2)$
150°	${5π}/6$	$(-{√3}/2, 1/2)$
180°	π	(-1, 0)
210°	${7}/6$	$(-{√3}/2, -1/2)$
225°	${5π}/4$	$(-{√2}/2, -{√2}/2)$
240°	${4π}/3$	$(-1/2, -{√3}/2)$
270°	${3π}/2$	(0, -1)
300°	${5π}/3$	$(1/2, -{√3}/2)$
315°	${7π}/4$	$({√2}/2, -{√2}/2)$
330°	${11π}/6$	$({√3}/2, -1/2)$

Nun, Sie können zwar gerne versuchen, sich all diese Koordinaten und Winkel zu merken, aber das ist eine Menge Zeug, das man sich merken muss.

Glücklicherweise gibt es einen Trick, der Ihnen helfen kann, sich die wichtigsten Teile des Einheitskreises zu merken.

Schauen Sie sich die obigen Koordinaten an und Sie werden ein klares Muster erkennen: alle Punkte (außer denen bei 0°, 90°, 270° und 360°) wechseln zwischen nur drei Werten (ob positiv oder negativ):

• $1/2$
• ${√2}/2$
• ${√3}/2$

Jeder Wert entspricht einer kurzen, mittleren oder langen Linie für Kosinus und Sinus:

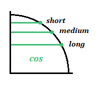
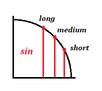
Hier steht, was diese Längen bedeuten:

• Kurze waagerechte oder senkrechte Linie = $1/2$
• Mittlere waagerechte oder senkrechte Linie = ${√2}/2$
• Lange waagerechte oder senkrechte Linie = ${√3}/2$

Wenn Sie zum Beispiel versuchen, $\cos{π/3}$ zu lösen, sollten Sie sofort wissen, dass dieser Winkel (der gleich 60° ist) eine kurze waagerechte Linie auf dem Einheitskreis anzeigt. Daher muss die zugehörige x-Koordinate gleich $1/2$ sein (ein positiver Wert, da $π/3$ einen Punkt im ersten Quadranten des Koordinatensystems erzeugt).

Schließlich ist es zwar hilfreich, sich alle Winkel in der obigen Tabelle einzuprägen, aber die mit Abstand wichtigsten Winkel sind die folgenden, die man sich merken sollte:

• 30° / $π/6$
• 45° / $π/4$
• 60° / $π/3$

Behandeln Sie Ihre negativen und positiven Kabel wie Kabel, die Sie möglicherweise töten können, wenn sie falsch angeschlossen sind.

#2: Lernen Sie, was negativ und was positiv ist

Es ist wichtig, positive und negative x- und y-Koordinaten unterscheiden zu können, damit Sie den richtigen Wert für ein Trigonometrieproblem finden. Zur Erinnerung: Ob eine Koordinate auf dem Einheitskreis positiv oder negativ ist, hängt davon ab, in welchen Quadranten (I, II, III oder IV) der Punkt fällt:

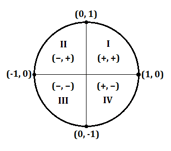
Hier ist eine Tabelle, die zeigt, ob eine Koordinate positiv oder negativ ist, basierend auf dem Quadranten, in dem ein bestimmter Winkel (in Grad oder Bogenmaß) liegt:

Quadrant	X-Koordinate (Cosinus)	Y-Koordinate (Sinus)
I	+	+
II	–	+
III	–	–
IV	+	–

Beispiel, Nehmen wir an, Sie bekommen in einem Mathe-Test die folgende Aufgabe gestellt:

$\cos210°$

Bevor Sie überhaupt versuchen, sie zu lösen, sollten Sie erkennen können, dass die Antwort eine negative Zahl sein wird, da der Winkel 210° in den Quadranten III fällt (wo x-Koordinaten immer negativ sind).

Nun können Sie mit dem Trick aus Tipp 1 herausfinden, dass ein Winkel von 210° eine lange horizontale Linie erzeugt. Daher lautet unsere Antwort wie folgt:

$\cos210°=-{√3}/2$

#3: Wissen, wie man den Tangens löst

Zuletzt ist es wichtig zu wissen, wie man all diese Informationen über den Trigonometriekreis und Sinus und Kosinus verwendet, um den Tangens eines Winkels lösen zu können.

In der Trigonometrie findet man den Tangens eines Winkels θ (entweder in Grad oder im Bogenmaß), indem man einfach den Sinus durch den Kosinus dividiert:

$\tanθ={\sinθ}/{\cosθ}$

Sagen wir zum Beispiel, dass Sie versuchen, diese Aufgabe zu lösen:

$\tan300°$

Der erste Schritt besteht darin, eine Gleichung in Form von Sinus und Kosinus aufzustellen:

$\tan300°={\sin300°}/{\cos300°}$

Nun müssen wir, um den Tangens zu lösen, den Sinus und Kosinus von 300° finden. Sie sollten schnell erkennen können, dass der Winkel 300° in den vierten Quadranten fällt, was bedeutet, dass der Kosinus bzw. die x-Koordinate positiv und der Sinus bzw. die y-Koordinate negativ sein wird.

Sie sollten auch gleich wissen, dass der Winkel 300° eine kurze horizontale Linie und eine lange vertikale Linie erzeugt. Daher wird der Kosinus (die horizontale Linie) gleich $1/2$ und der Sinus (die vertikale Linie) gleich $-{√3}/2$ sein (ein negativer y-Wert, da dieser Punkt im Quadranten IV liegt).

Um nun den Tangens zu finden, muss man nur noch einstecken und lösen:

$\tan300°={-{√3}/2}/{1/2}$

$$\tan300°=-√3$

Zeit, deine Mathekenntnisse zu trainieren!

Einheitskreis-Übungsaufgabensatz

Nun, da Sie wissen, wie der Einheitskreis aussieht und wie man ihn verwendet, wollen wir das Gelernte mit ein paar Übungsaufgaben testen.

Fragen

1. $\sin45°$
2. $cos240°$
3. $\cos{5π}/3$
4. $\tan{2π}/3$

Antworten

1. ${√2}/2$
2. $-1/2$
3. $1/2$
4. $-√3$

Antwort-Erläuterungen

#1: $\sin45°$

Bei dieser Aufgabe gibt es zwei Informationen, die Sie auf Anhieb erkennen können sollten:

• Die Antwort wird positiv sein, da der Winkel 45° im Quadranten I liegt und der Sinus eines Winkels gleich der y-Koordinate ist

• Der Winkel 45° erzeugt eine mittellange senkrechte Linie (für den Sinus)

Da 45° eine positive, mittellange Linie angibt, ist die richtige Antwort ${√2}/2$.

Wenn Sie sich nicht sicher sind, wie Sie dies herausfinden können, zeichnen Sie ein Diagramm, um zu bestimmen, ob die Länge der Linie kurz, mittel oder lang sein wird.

#2: $\cos240°$

Wie bei Problem #1 oben, gibt es zwei Informationen, die Sie bei diesem Problem schnell erfassen sollten:

• Die Antwort wird negativ sein, da der Winkel 240° im Quadranten III liegt und der Kosinus eines Winkels gleich der x-Koordinate ist

• Der Winkel 240° erzeugt eine kurze horizontale Linie (für den Kosinus)

Da 240° eine negative, kurze Linie anzeigt, ist die richtige Antwort $-1/2$.

#3: $\cos{5π}/3$

Im Gegensatz zu den obigen Aufgaben wird bei dieser Aufgabe das Bogenmaß anstelle von Grad verwendet. Obwohl das Problem dadurch kniffliger aussieht, verwendet es in Wirklichkeit die gleichen grundlegenden Schritte wie die anderen beiden Probleme.

Zunächst sollten Sie erkennen, dass der Winkel ${5π}/3$ im Quadranten IV liegt, so dass die x-Koordinate, also der Kosinus, eine positive Zahl ist. Sie sollten auch in der Lage sein zu erkennen, dass ${5π}/3$ eine kurze horizontale Linie erzeugt.

Damit haben Sie genug Informationen, um festzustellen, dass die Antwort $1/2$ ist.

#4: $\tan{2π}/3$

Dieses Problem befasst sich mit dem Tangens anstelle von Sinus oder Kosinus, was bedeutet, dass es ein wenig mehr Mathematik von unserer Seite erfordert. Erinnern Sie sich zunächst an die Grundformel für die Bestimmung des Tangens:

$$tan θ={\sin θ}/{\cos θ}$

Nun nehmen wir den Grad, den wir erhalten haben -${2π}/3$ – und setzen ihn in diese Gleichung ein:

$$tan {2π}/3={\sin {2π}/3}/{\cos {2π}/3}$

Sie sollten jetzt in der Lage sein, den Sinus und den Kosinus separat zu lösen, indem Sie das verwenden, was Sie sich über den Einheitskreis gemerkt haben. Da der Winkel ${2π}/3$ im Quadranten II liegt, ist die x-Koordinate (bzw. der Kosinus) negativ und die y-Koordinate (bzw. der Sinus) positiv.

Als Nächstes sollten Sie allein anhand des Winkels feststellen können, dass die horizontale Linie eine kurze Linie und die vertikale Linie eine lange Linie ist. Das heißt, der Kosinus ist gleich $-1/2$ und der Sinus ist gleich ${√3}/2$.

Nun, da wir diese Werte herausgefunden haben, müssen wir sie nur noch in unsere Anfangsgleichung einsetzen und den Tangens lösen:

$\tan {2π}/3={{√3}/2}/{-1/2}$

$$\tan {2π}/3=-√3$

Wie geht es weiter?

Wenn Sie bald den SAT oder ACT ablegen, müssen Sie ein wenig Trigonometrie beherrschen, damit Sie im Matheteil gut abschneiden können. Werfen Sie einen Blick auf unsere Experten-Leitfäden zu Trigonometrie im SAT und ACT, damit Sie genau lernen können, was Sie für den Testtag wissen müssen!

Neben dem Auswendiglernen des Einheitskreises ist es eine gute Idee, zu lernen, wie man Zahlen einträgt und wie man Antworten einträgt. Lesen Sie unsere Leitfäden, um alles über diese beiden nützlichen Strategien zu erfahren, die Sie bei jedem Mathe-Test anwenden können – auch beim SAT und ACT!

Haben Sie Freunde, die auch Hilfe bei der Testvorbereitung brauchen? Teilen Sie diesen Artikel!