Volumenberechnung
Diese Seite erklärt, wie man das Volumen von festen Objekten berechnet, d.h. wie viel in ein Objekt hineinpasst, wenn man es z.B. mit einer Flüssigkeit füllt.
Fläche ist das Maß dafür, wie viel Raum in einem zweidimensionalen Objekt vorhanden ist (mehr dazu auf unserer Seite: Fläche berechnen).
Volumen ist das Maß dafür, wie viel Raum in einem dreidimensionalen Objekt vorhanden ist. Unsere Seite über dreidimensionale Formen erklärt die Grundlagen solcher Formen.
In der realen Welt ist die Berechnung des Volumens wahrscheinlich nicht etwas, das Sie so oft verwenden werden wie die Berechnung der Fläche.
Es kann aber dennoch wichtig sein. Wenn Sie in der Lage sind, das Volumen zu berechnen, können Sie zum Beispiel herausfinden, wie viel Platz Sie beim Umzug haben, wie viel Platz Sie im Büro brauchen oder wie viel Marmelade in ein Glas passt.
Es kann auch nützlich sein, um zu verstehen, was die Medien meinen, wenn sie über die Kapazität eines Staudamms oder den Durchfluss eines Flusses sprechen.
Ein Hinweis zu den Einheiten
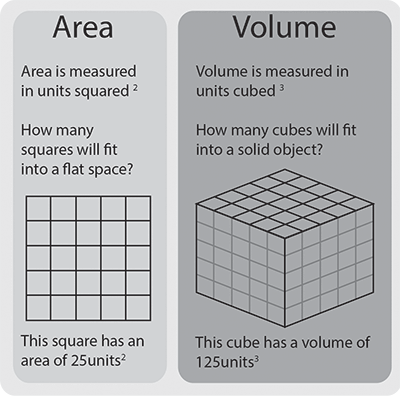
Die Fläche wird in quadratischen Einheiten ausgedrückt, da sie aus zwei Maßen besteht, die miteinander multipliziert werden.
Das Volumen wird in kubischen Einheiten ausgedrückt, da es die Summe von drei Maßen ist (Länge, Breite und Tiefe), die miteinander multipliziert werden. Kubische Einheiten sind cm3, m3 und Kubikfuß.
WARNUNG!
Volumen kann auch als Flüssigkeitsvolumen ausgedrückt werden.
Metrisches System
Im metrischen System wird das Flüssigkeitsvolumen in Litern gemessen, was direkt mit dem kubischen Maß vergleichbar ist, da 1ml = 1cm3. 1 Liter = 1.000 ml = 1.000cm3.
Imperiales/englisches System
Im imperialen/englischen System sind die äquivalenten Maße fluid ounces, pints, quarts und gallons, die nicht einfach in Kubikfuß umgerechnet werden können. Es ist daher am besten, sich entweder an flüssige oder feste Volumeneinheiten zu halten.
Weitere Informationen finden Sie auf unserer Seite über Maßsysteme
Grundlegende Formeln zur Berechnung des Volumens
Volumen von rechteckigen Festkörpern

Während die Grundformel für den Flächeninhalt einer rechteckigen Form Länge × Breite ist, ist die Grundformel für das Volumen Länge × Breite × Höhe.
Wie Sie die verschiedenen Dimensionen bezeichnen, ändert nichts an der Berechnung: Sie können z. B. „Tiefe“ statt „Höhe“ verwenden. Wichtig ist, dass die drei Dimensionen miteinander multipliziert werden. Sie können in beliebiger Reihenfolge multiplizieren, es ändert nichts an der Antwort (mehr dazu auf unserer Seite zur Multiplikation).
Eine Schachtel mit den Maßen 15cm Breite, 25cm Länge und 5 cm Höhe hat ein Volumen von:
15 × 25 × 5 = 1875cm3
Volumen von Prismen und Zylindern
Diese Grundformel lässt sich auch auf das Volumen von Zylindern und Prismen erweitern. Statt eines rechteckigen Endes hat man einfach eine andere Form: einen Kreis für Zylinder, ein Dreieck, Sechseck oder ein beliebiges anderes Vieleck für ein Prisma.
Für Zylinder und Prismen ist das Volumen die Fläche einer Seite multipliziert mit der Tiefe oder Höhe der Form.
Die Grundformel für das Volumen von Prismen und Zylindern lautet also:
Fläche der Endform × Höhe/Tiefe des Prismas/Zylinders.
Volumen von Kegeln und Pyramiden
Das gleiche Prinzip wie oben (Breite × Länge × Höhe) gilt für die Berechnung des Volumens eines Kegels oder einer Pyramide, außer dass das Volumen nur ein Teil des Gesamtvolumens ist, das es wäre, wenn sie durchgehend die gleiche Form hätten, weil sie in einem Punkt enden.
Das Volumen eines Kegels oder einer Pyramide ist genau ein Drittel dessen, was es für einen Kasten oder Zylinder mit derselben Grundfläche wäre.
Die Formel lautet also:
Fläche der Grund- oder Endform × Höhe des Kegels/der Pyramide × 1/3
Wenn Sie sich nicht mehr daran erinnern können, wie man die Fläche eines Kreises oder Dreiecks berechnet, gehen Sie zurück zu unserer Seite Flächenberechnung.
Zum Beispiel, um das Volumen eines Kegels mit einem Radius von 5 cm und einer Höhe von 10 cm zu berechnen:
Der Flächeninhalt eines Kreises = πr2 (wobei π (pi) etwa 3,14 ist und r der Radius des Kreises).
In diesem Beispiel ist die Fläche der Basis (des Kreises) = πr2 = 3,14 × 5 × 5 = 78,5cm2.
78,5 × 10 = 785
785 × 1/3 = 261,6667cm3

Volumen einer Kugel
Wie bei einem Kreis braucht man π (pi), um das Volumen einer Kugel zu berechnen.
Die Formel lautet 4/3 × π × Radius3.
Sie fragen sich vielleicht, wie Sie den Radius einer Kugel berechnen können. Abgesehen davon, eine Stricknadel durchzustechen (effektiv, aber tödlich für die Kugel!), gibt es einen einfacheren Weg.
Sie können den Abstand um die breiteste Stelle der Kugel direkt messen, zum Beispiel mit einem Maßband. Dieser Kreis ist der Umfang und hat den gleichen Radius wie die Kugel selbst.
Den Umfang eines Kreises berechnet man als 2 x π x Radius.
Um den Radius aus dem Umfang zu berechnen, muss man:
Den Umfang durch (2 x π) dividieren.
Arbeitsbeispiele: Volumen berechnen
Beispiel 1

Berechnen Sie das Volumen eines Zylinders mit einer Länge von 20cm, dessen kreisförmiges Ende einen Radius von 2,5cm hat.
Berechnen Sie zunächst den Flächeninhalt eines der kreisförmigen Enden des Zylinders.
Der Flächeninhalt eines Kreises ist πr2 (π × Radius × Radius). π (pi) ist ungefähr 3,14.
Der Flächeninhalt eines Endes ist also:
3,14 x 2,5 x 2,5 = 19,63cm2
Das Volumen ist der Flächeninhalt eines Endes multipliziert mit der Länge und beträgt also:
19.63cm2 x 20cm = 392.70cm3

Beispiel 2
Welches ist vom Volumen her größer, eine Kugel mit Radius 2cm oder eine Pyramide mit quadratischer Grundfläche von 2,5cm und Höhe von 10cm?
Berechnen Sie zunächst das Volumen der Kugel.
Das Volumen einer Kugel ist 4/3 × π × Radius3.
Das Volumen der Kugel ist also:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51cm3
Berechne dann das Volumen der Pyramide.
Das Volumen einer Pyramide ist 1/3 × Fläche der Grundfläche × Höhe.
Fläche der Basis = Länge × Breite = 2,5cm × 2,5cm = 6,25cm2
Das Volumen ist also 1/3 x 6,25 × 10 = 20,83cm3
Die Kugel ist also vom Volumen her größer als die Pyramide.
Volumen unregelmäßiger Körper berechnen
Genauso wie man den Flächeninhalt unregelmäßiger zweidimensionaler Formen berechnen kann, indem man sie in regelmäßige Formen zerlegt, kann man dasselbe tun, um das Volumen unregelmäßiger Körper zu berechnen. Teilen Sie den Körper einfach in kleinere Teile auf, bis Sie nur noch Körper erreichen, mit denen Sie leicht arbeiten können.
Arbeitsbeispiel
Berechnen Sie das Volumen eines Wasserzylinders mit einer Gesamthöhe von 1m, einem Durchmesser von 40cm und dessen oberer Teil halbkugelförmig ist.

Zunächst teilt man die Form in zwei Abschnitte, einen Zylinder und eine Halbkugel (halbe Kugel).
Das Volumen einer Kugel ist 4/3 × π × Radius3. In diesem Beispiel ist der Radius 20cm (der halbe Durchmesser). Da der Kreisel halbkugelförmig ist, ist sein Volumen halb so groß wie das einer Vollkugel. Das Volumen dieses Teils der Form ist also:
0,5 × 4/3 × π × 203 = 16.755,16cm3
Das Volumen eines Zylinders ist Grundfläche × Höhe. Hier ist die Höhe des Zylinders die Gesamthöhe abzüglich des Radius der Kugel, also 1m – 20cm = 80cm. Der Flächeninhalt der Grundfläche ist πr2.
Das Volumen des zylindrischen Teils dieser Form ist also:
80 × π × 20 × 20 = 100.530,96cm3
Das Gesamtvolumen dieses Wasserbehälters ist also:
100.530,96 + 16.755,16 = 117.286,12cm3.
Das ist eine ziemlich große Zahl, deshalb kann man sie lieber in 117,19 Liter umrechnen, indem man sie durch 1.000 teilt (denn in einem Liter sind 1000cm3). Es ist jedoch völlig korrekt, es in cm3 auszudrücken, da die Aufgabe nicht verlangt, dass die Antwort in einer bestimmten Form ausgedrückt wird.
Zusammenfassend…
Mit diesen Prinzipien sollten Sie nun in der Lage sein, wenn nötig, das Volumen von fast allem in Ihrem Leben zu berechnen, sei es eine Verpackungskiste, ein Zimmer oder ein Wasserzylinder.