Was ist der Unterschied zwischen PNP und NPN?

Dieser Artikel erschien in Microwaves & RF und wurde hier mit Genehmigung veröffentlicht.

Was Sie lernen werden:

• Der maximale Durchsatz eines Kanals als Funktion der Symbolrate und Bandbreite.
• Der maximale Durchsatz eines Kanals als Funktion von Rauschstörungen.
• Wie Durchsatzbetrachtungen den ganzen Weg zurück zum Benutzer gehen.

Es ist eine sehr einfache und normale Sache, sich auf die Haupteigenschaften der Hauptkomponenten eines Kommunikationssystems oder einer Verbindung zu konzentrieren und andere Elemente und Themen als peripher und nicht so wichtig zu betrachten. Dass dies bei Satellitenkommunikationsverbindungen, insbesondere bei entfernten mobilen Verbindungen, überraschend häufig vorkommt, ist der Grund für diesen Beitrag.

Hier ist eine hypothetische Situation. Sie sind ein Soldat. Sie sind in einer gebirgigen Gegend des Nahen Ostens im Einsatz und haben ein älteres Intelsat-Satellitenterminal dabei, um sofortigen Zugang zurück zum Hauptquartier zu haben, und das Hauptquartier hat einen 72-MHz-Transponder für Ihre ausschließliche Nutzung geleast.

Ein netter, sicherer Ort ist eine Höhle, also ziehen Sie ein Kommunikationskabel zum Satellitenterminal am Höhleneingang und lehnen sich zurück, um sich bei Ihrer Workstation einzuchecken, die mit einem QPSK-Modem (Quadrature Phase Shift Keying) mit dem Terminal verbunden ist. Das Einchecken ist gut, aber die Verbindung ist lausig. Die Satellitenfirma garantiert Ihnen 72 Mb/s (1 Bit pro Hz), aber Sie bekommen kaum weniger als 35 Mb/s. Hätten Sie sich ein neueres Terminal zulegen sollen? Sollten Sie ein anderes System verwenden?

Nyquist Maximale Datenraten

Die eigentliche Antwort ist das, was Harry Nyquist und Claude Shannon über maximale Datenraten über jeden Kanal sagten, einschließlich dieses Kommunikationskabels. Harry Nyquist stellte fest, wie ausführlich dokumentiert wurde1, dass die maximale Anzahl von Bits, die man über einen Kanal bekommen kann (Rauschen nicht berücksichtigt), ist:

Max R = 2 H Log2V

wobei H die Kanalbandbreite und V die Anzahl der diskreten Symbole ist (binäre Phasenumtastung, oder BPSK, ist 2, QPSK ist 4, usw.).

Wenn Sie mit log2 nicht vertraut sind, ist es nicht schwierig, wenn Sie sich einmal daran gewöhnt haben. Der log2V ist einfach der Exponent, auf den 2 erhöht werden muss, um V zu entsprechen. Wenn also V BPSK (2) ist, dann ist der Ausdruck log2V einfach 1, da 21 eigentlich 2 ist; und wenn V QPSK (4) ist, dann ist der Ausdruck log2V 2, da 22 eigentlich 4 ist, und so weiter.

Wenn Sie ein 10-MHz-Cat-3-Kabel verwenden, dann ist die maximale Datenrate INTO des Satellitenterminals BPSK 20 Mb/s, QPSK 40 Mb/s und 8PSK 30 Mb/s, als eine Funktion der log2-Beziehungen. Abbildung 1 zeigt die Anzahl der Zustände und deren log zur Basis 2 äquivalent. Daher liegt die Nyquist-Grenze bei Verwendung des QPSK-Modems bei 40 Mb/s.

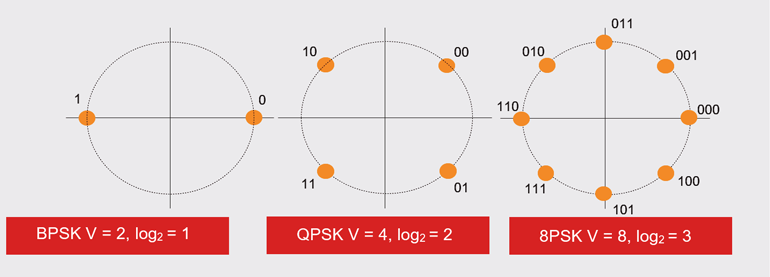1. BPSK, mit zwei Zuständen, hat einen log2-Wert von 1; QPSK, mit vier Zuständen, hat einen log2-Wert von 2; und so weiter.

Shannon Maximale Datenraten

Nun, Harry Nyquist arbeitete an dem Problem der maximalen Datenraten ohne Berücksichtigung des Rauschens, während Claude Shannon es strikt als eine Funktion des Rauschens bearbeitete. Seine Gleichung2 besagt:

Max R = H log2 (1 + SNR)

wobei H wiederum die Kanalbandbreite ist und das SNR die Signalleistung geteilt durch die Rauschleistung ist, im Allgemeinen angegeben in dB. Nehmen wir an, dass das SNR auf demselben Cat-3-Kabel etwa 30 dB oder 1.000 in rohen Zahlen beträgt (das SNR muss in seinen rationalen Wert umgewandelt werden, um ein Exponential zu berechnen). Da wir die Skala der 2er-Exponentiale nach oben durchlaufen haben, können wir das einfach weiter tun. Abbildung 2 zeigt diese Progression.

Wenn wir der Einfachheit halber ein wenig abrunden, ist 1.001 näher an 1.024 als jede andere Schrittweite und 2 hoch 10 ergibt einen Wert, der weit näher an jedem anderen Exponenten liegt. Wenn Claude Shannon sagt, dass man mit einem Cat-3-Kabel mit 10 MHz Bandbreite eine Datenrate von 10 x 106 (10) = 100 Mb/s erreichen kann.

Wenn Claude Shannon sagt, dass man eine maximale Datenrate von 100 Mb/s in ein Satellitenkommunikationsterminal bekommen kann, und Harry Nyquist sagt, dass man nur 40 Mb/s von und zu seiner mit QPSK ausgestatteten Workstation bekommen kann, wer hat dann Recht?

Lassen Sie uns eine andere Analogie betrachten. Die Universität von Notre Dame hat eine akademisch eingeschränkte, aber relativ gute Fußballmannschaft. Auf der anderen Seite hat sie eine großartige Marschkapelle, denn hervorragende Musiker sind häufig hervorragende Highschool-Schüler. Um auf das Spielfeld zu gelangen, muss die Band durch zwei Torbögen marschieren, von denen einer 15 Mitglieder nebeneinander erlaubt und einer 10. Wie viele Mitglieder nebeneinander stellt sich die Band auf? Nun, auf die gleiche Art und Weise, Nyquist und Shannon konkurrieren nicht. Sie sind nur zwei verschiedene Tore mit zwei verschiedenen Einschränkungen.

Es ist nicht nur das Hauptsystem. Es sind die „goes-intas“ und die „goes-outas“, bis hin zu den Händen, die auf der Tastatur tippen. Und die Originalarbeiten des Physikers Nyquist3 und des Mathematikers/Ingenieurs Shannon4 haben uns immer noch etwas zu sagen.

1. Ein Beispiel für die Gleichung finden Sie in jeder Ausgabe von Data and Computer Communications von William Stallings unter Nyquist Bandwidth. Hinweis: Verschiedene Autoren verwenden unterschiedliche Buchstaben für die Bezeichnung von Datenrate, Bandbreite usw.

2. Wie bei der Nyquist-Gleichung, die in jeder Ausgabe von Data and Computer Communications von William Stallings zu finden ist, wird diese unter Shannon Capacity Formula aufgeführt. Hinweis: Verschiedene Autoren verwenden unterschiedliche Buchstaben zur Bezeichnung von Datenrate, Bandbreite usw.

3. Bestimmte Themen der Telegraphenübertragungstheorie (die das Limit implizierten) wurden auf der Winter Convention der AIEE, New York, N.Y., vom 13. bis 17. Februar 1928 vorgestellt. Es wurde als „Classic Paper“ in den Proceedings of the IEEE im Februar 2002 wiederveröffentlicht.

4. „Communications in the Presence of Noise“ wurde in den Proceedings of the IRE im Januar 1949 veröffentlicht, neun Jahre nachdem es geschrieben wurde.