Wie man die Basis versteht (Lineare Algebra)

Beim Unterrichten der linearen Algebra, wird das Konzept der Basis oft übersehen. Meine Nachhilfeschüler konnten zwar lineare Unabhängigkeit und Spanne verstehen, aber sie sahen die Basis, wie man ein UFO sehen könnte: verwirrend und fremd. Und das ist nicht gut, denn die Basis dient als Ausgangspunkt für einen Großteil der linearen Algebra.

Wir brauchen immer einen Ausgangspunkt, ein Fundament, auf dem alles andere aufbaut. Wörter können nicht ohne die Grundlage eines Alphabets geschrieben werden. Alte Zivilisationen glaubten, dass das Universum aus den 4 klassischen Elementen – Wasser, Erde, Feuer und Luft – gebildet wurde (vor langer Zeit…). Und Vektorräume, die natürliche Heimat der linearen Algebra, haben die Basis als ihr Fundament.

Ich werde die Basis konzeptionell anhand einer Analogie zur Malerei erklären. Diese Analogie wurde in zwei früheren Artikeln verwendet, um zwei andere Konzepte aus der linearen Algebra zu erklären, nämlich lineare Unabhängigkeit/Abhängigkeit und Spannweite. Ich empfehle, diese Artikel zuerst zu lesen, da beide Konzepte später noch auftauchen werden.

Die Basis der Farben

Anstatt Mathe zu machen, nehmen Sie an, Sie sind ein Maler, der bereit ist, ein Meisterwerk auf seine Leinwand zu malen. Zuerst müssen Sie Farbe kaufen. Wie viele Farben sollten Sie kaufen?

Natürlich ist es eine schlechte Idee, ein Gemälde zu malen, indem Sie zu Home Depot fahren und jeweils eine Dose Farbe für all die Tausende von Farben kaufen, die sie haben. Sie brauchen nicht dreißig verschiedene Blautöne, von Azurblau über Bergblau bis hin zu Siegesblau (Idee: Erstellen Sie eine Farbe namens „Defeat Blue“). Sie müssen nur blaue Farbe und ein paar andere Farben kaufen.

Wenn Sie ein geiziger Maler sind, könnten Sie sogar sagen, dass Sie nur 5 Farben kaufen müssen, um ein Bild zu malen: Rot, Gelb, Blau, Weiß und Schwarz. Klar, grün wäre schön, und rosa wäre cool, aber Sie müssen nicht unbedingt rosa und grüne Farbe kaufen. Schließlich können Sie rote und weiße Farbe kombinieren, um rosa zu machen, oder gelbe und blaue Farbe, um grün zu machen.

Rot, gelb, blau, weiß und schwarz sind die minimale Menge an Farben, die Sie brauchen, um jede andere Farbe zu machen. Man könnte sagen, dass diese fünf Farben eine Basis für das gesamte Farbspektrum bilden.

Da man jede andere Farbe mit Mischungen dieser fünf Farben herstellen kann, könnte man sagen, dass diese fünf Farben die Menge aller Farben umfassen. Außerdem ist jede Farbe in der Menge notwendig: Sie brauchen weiße Farbe, weil keine Menge gelber, roter, schwarzer oder blauer Farbe zusammengemischt jemals weiße Farbe ergeben wird. Mit anderen Worten: Rot, Gelb, Blau, Weiß und Schwarz sind unabhängig voneinander.

Nennen wir Ihre Menge an Farben Ihre Palette. Damit Ihre Palette eine Grundlage für alle Farben bildet, müssen zwei Bedingungen erfüllt sein:

1. Die Palette umfasst die Menge aller Farben.
2. Alle Farben in der Palette sind unabhängig voneinander.

Wir haben gerade gesehen, dass Rot, Gelb, Blau, Weiß und Schwarz beide Bedingungen erfüllen. Im Gegensatz dazu sind hier Beispiele für Paletten, die keine Basis sind:

• Rot, Blau, Weiß. Dies verstößt gegen Bedingung 1. Diese Menge umfasst nicht alle Farben. Viele Farben wie Gelb oder Grün sind unmöglich mit Farben aus dieser Menge herzustellen.
• Rot, Orange, Gelb, Grün, Blau, Lila, Weiß, Schwarz. Dies verstößt gegen Bedingung 2. Diese Farben umfassen zwar alle Farben, aber sie sind nicht unabhängig. Lila ist eine Kombination aus Rot und Blau, Grün eine Kombination aus Gelb und Blau, und so weiter.

Die Basis eines Vektorraums

Vektorräume sind abstrakter als Bilder, aber sie verwenden die Basis ähnlich. Ein Vektorraum ist eine Menge von Vektoren, in der man Vektoren zusammenfügen und skalieren kann. Zum Beispiel ist die 2-D-Ebene (auch als R² bekannt) ein Vektorraum. Sie ist die Menge aller „2-dimensionalen“ Vektoren, die man sich als Vektoren mit einer x-Koordinate und einer y-Koordinate vorstellen kann.

Genauso wie wir eine Basis für die Menge aller Farben erstellt haben, können wir eine Menge von Vektoren erstellen, die eine Basis von R² bilden. Die Anforderungen an die Basis sind fast die gleichen wie bei unserer Basis für Farben.

Basis: Eine Menge von n Vektoren, {v₁, v₂, … vₙ}, ist eine Basis eines Raumes S, wenn diese beiden Bedingungen wahr sind:

1. {v₁, v₂, …vₙ} sind linear unabhängig.
2. {v₁, v₂,…vₙ} spannen die Menge S auf. Mit anderen Worten: Span{v₁,v₂,…vₙ}=S

Nehmen wir zum Beispiel die Vektoren (0,1) und (1,0), die unten in grün eingezeichnet sind. Diese Vektoren sind linear unabhängig, da es keine Möglichkeit gibt, (0,1) in (1,0) zu skalieren. Außerdem überspannen diese beiden Vektoren die gesamte 2-D-Ebene, da man jeden Punkt im 2-D-Raum als Linearkombination von (0,1) und (1,0) umschreiben kann:

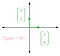
(0,1) und (1,0) bilden also eine Basis von R² (Diese spezielle Basis von (0,1) und (1,0) wird Standardbasis genannt). Dies ist jedoch nicht die einzige mögliche Basis von R². Schauen Sie sich die Vektoren (1,1) und (-1,1) an, die unten grafisch dargestellt sind. Die rosafarbenen Vektoren repräsentieren einige verschiedene Linearkombinationen:

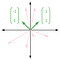
Diese beiden Vektoren sind ebenfalls linear unabhängig, da man den einen Vektor nicht in den anderen skalieren kann. Aus den rosafarbenen Linearkombinationen ist auch ersichtlich, dass (1,1) und (-1,1) ganz R² aufspannen. Daher bilden (1,1) und (-1,1) eine weitere Basis für R².

Dies ist ein Punkt, an dem sich Vektorräume stark von der Farbanalogie unterscheiden. Bei Farben haben wir wirklich nur die Basis von Gelb, Blau, Rot, Schwarz und Weiß. Aber in der Welt der Vektorräume hat jeder Raum eine unendliche Anzahl von Basen, aus denen man wählen kann. Im Allgemeinen ist eine Basis die kleinstmögliche Menge von Vektoren, die einen Raum aufspannen kann. Sie ist das vektorielle Äquivalent dazu, dass man mit seiner Farbe geizt und nur die minimal benötigten Farben kauft.

Die Basis hilft uns auch, die zugrundeliegende Struktur eines Vektorraums herauszufinden. Wir wissen zum Beispiel, dass jede Basis von R² aus genau zwei Vektoren besteht, wie die beiden Basen, die wir zuvor gefunden haben. Allgemein:

• Für einen Raum S haben alle Basen von S die gleiche Anzahl von Vektoren. Dies wurde erstmals von Georg Hamel bewiesen. Wenn eine Basis für S aus 4 Vektoren besteht, dann besteht jede Basis für S aus 4 Vektoren.
• Eine Basis für einen Rⁿ-Raum besteht aus n Vektoren. Jede Basis für R³ (3-dimensionaler Raum) besteht aus 3 Vektoren. Jede Basis für R⁵ (5-dimensionaler Raum, fragen Sie nicht) besteht aus 5 Vektoren.

Warum die Basis wichtig ist (Lineare Transformationen)

Für sich genommen hat die Basis keine große Bedeutung. Dennoch wollen wir kurz darauf eingehen, warum die Basis für die lineare Algebra so wichtig ist.

Wir können einen Vektorraum nehmen und ihn transformieren, wobei „transformieren“ hier bedeutet, den Raum zu strecken, zu kippen oder zu drehen. Bei der Arbeit mit linearer Algebra ist das Transformieren eines Vektorraums so alltäglich wie das Atmen. Nehmen wir an, ich möchte den Graphen A in den Graphen B transformieren:

Jeder Graph hat seine eigene Basis (die rosa und blauen Vektoren). Wichtig ist, dass sowohl Graph A als auch Graph B nur zwei verschiedene Arten sind, denselben Raum mit unterschiedlichen Basen darzustellen. Das ist so, als würde man dasselbe Buch lesen, aber in zwei verschiedenen Sprachen, z. B. Spanisch und Französisch.

Die Verschiebung von Graph A nach Graph B wird als lineare Transformation des Graphen bezeichnet. Eine lineare Transformation wirkt wie ein Übersetzer: Sie nimmt jeden Punkt in Graph B und verschiebt ihn zu jedem entsprechenden Punkt in Graph A. Sie nimmt das französische Wort und verschiebt es ins Spanische. Aber wir tauchen jetzt in die Welt der linearen Transformationen ein, und das kann ein anderes Mal erklärt werden.

Abschluss

Wir haben jetzt ein tieferes Verständnis für drei Konzepte der linearen Algebra: Basis, lineare Unabhängigkeit/Abhängigkeit und Spannweite. Diese Konzepte sind grundlegend für die lineare Algebra. Lineare Unabhängigkeit/Abhängigkeit sagt Ihnen, welche Vektoren in einer Menge von Vektoren notwendig sind. Die Spanne sagt Ihnen, wie viele mögliche Kombinationen von Vektoren Sie erstellen können. Und schließlich sagt Ihnen die Basis, welche kleinste Menge von Vektoren nötig ist, um einen Vektorraum aufzuspannen, und damit die Struktur dieses Raumes.

Die Beherrschung dieser Konzepte gibt Ihnen die Grundlage, die Sie für ein konkretes Verständnis der linearen Algebra benötigen. Schließlich kann ein Haus nicht auf einem wackeligen Fundament stehen, und wir können die Lineare Algebra nicht ohne eine Basis verstehen. Vielen Dank für die Lektüre!