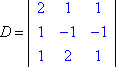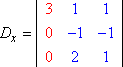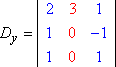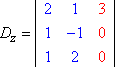Cramersche Regel

Zurück zum Lektionsindex | Lektionen der Reihe nach bearbeiten | Druckfreundliche Seite

Cramersche Regel

Gegeben ein System linearer Gleichungen, Cramer’s Rule ist ein praktischer Weg, um nur eine der Variablen zu lösen, ohne das ganze Gleichungssystem lösen zu müssen. Normalerweise wird die Cramersche Regel nicht auf diese Weise gelehrt, aber das soll der Sinn der Regel sein: Anstatt das gesamte Gleichungssystem zu lösen, können Sie die Cramersche Regel verwenden, um nur eine einzige Variable zu lösen.

Lassen Sie uns das folgende Gleichungssystem verwenden:

2x + y + z = 3
x – y – z = 0
x + 2y + z = 0

Wir haben die linke Seite des Systems mit den Variablen (die „Koeffizientenmatrix“) und die rechte Seite mit den Antwortwerten. Sei D die Determinante der Koeffizientenmatrix des obigen Systems, und sei Dx die Determinante, die durch Ersetzen der Werte der x-Spalte durch die Werte der Antwortspalte gebildet wird:

Gleichermaßen, Dy und Dz würden dann lauten: Copyright © Elizabeth Stapel 2004-2011 All Rights Reserved

Wenn man jede Determinante auswertet (mit der hier erklärten Methode), erhalten wir:

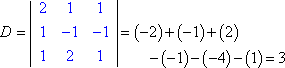
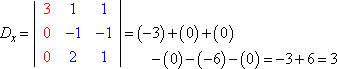
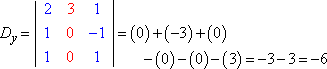
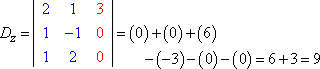
Die Cramersche Regel besagt, dass x = Dx ÷ D, y = Dy ÷ D, und z = Dz ÷ D. Das heißt:

x = 3/3 = 1, y = -6/3 = -2, und z = 9/3 = 3

Das ist alles, was die Cramersche Regel ausmacht. Um die gewünschte Variable zu finden (nennen Sie sie „ß“ oder „Beta“), werten Sie einfach den Quotienten der Determinante Dß ÷ D aus. (Bitten Sie mich nicht zu erklären, warum das funktioniert. Vertrauen Sie mir einfach, dass Determinanten viele Arten von Magie wirken können.)

• Bestimmen Sie im folgenden Gleichungssystem den Wert von z.

2x + y + z = 1
x – y + 4z = 0
x + 2y – 2z = 3

Um nur für z zu lösen, finde ich zuerst die Koeffizientendeterminante.

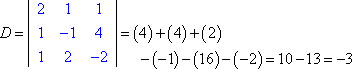
Dann bilde ich Dz, indem ich die dritte Wertespalte durch die Antwortspalte ersetze:

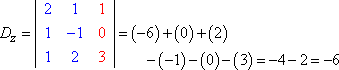
Dann bilde ich den Quotienten und vereinfache:

z = 2

Der Sinn der Cramerschen Regel ist, dass man nicht das ganze System lösen muss, um den einen Wert zu erhalten, den man braucht. Das hat mir bei einigen Physikprüfungen eine Menge Zeit gespart. Ich habe vergessen, woran wir gearbeitet haben (irgendetwas mit Drähten und Strömen, glaube ich), aber die Cramersche Regel war so viel schneller als jede andere Lösungsmethode (und Gott weiß, dass ich die zusätzliche Zeit brauchte). Lassen Sie sich nicht von all den tiefgestellten Indizes und so verwirren; die Regel ist wirklich ziemlich einfach. Sie wählen einfach die Variable aus, für die Sie lösen wollen, ersetzen die Wertespalte dieser Variable in der Koeffizienten-Determinante durch die Werte der Antwortspalte, werten diese Determinante aus und dividieren durch die Koeffizienten-Determinante. Das ist alles.

Was ist, wenn die Koeffizientendeterminante Null ist?

Was ist, wenn die Koeffizientendeterminante Null ist? Man kann nicht durch Null dividieren, was bedeutet das dann? Ich kann hier nicht auf die technischen Details eingehen, aber „D = 0“ bedeutet, dass das Gleichungssystem keine eindeutige Lösung hat. Das System kann inkonsistent sein (überhaupt keine Lösung) oder abhängig (eine unendliche Lösung, die als parametrische Lösung wie „(a, a + 3, a – 4)“ ausgedrückt werden kann). In Bezug auf die Cramersche Regel bedeutet „D = 0“, dass Sie eine andere Methode (z. B. Matrixreihenoperationen) verwenden müssen, um das System zu lösen. Wenn D = 0 ist, können Sie die Cramersche Regel nicht anwenden.

Top | Zurück zum Index