DeMorgan’s Theorems

Ein Mathematiker namens DeMorgan entwickelte ein Paar wichtiger Regeln bezüglich der Gruppenkomplementierung in der Booleschen Algebra.

Mit Gruppenkomplementierung meine ich das Komplement einer Gruppe von Termen, dargestellt durch einen langen Balken über mehr als einer Variablen.

Sie sollten sich aus dem Kapitel über logische Gatter daran erinnern, dass das Invertieren aller Eingänge eines Gatters die wesentliche Funktion dieses Gatters von UND zu ODER umkehrt, oder umgekehrt, und auch den Ausgang invertiert.

Ein ODER-Gatter, bei dem alle Eingänge invertiert sind (ein Negativ-ODER-Gatter), verhält sich also wie ein NAND-Gatter, und ein UND-Gatter, bei dem alle Eingänge invertiert sind (ein Negativ-AND-Gatter), verhält sich wie ein NOR-Gatter.

DeMorgans Theoreme geben dieselbe Äquivalenz in „umgekehrter“ Form an: dass die Invertierung des Ausgangs eines beliebigen Gatters zur gleichen Funktion führt wie der entgegengesetzte Gattertyp (UND vs. ODER) mit invertierten Eingängen:

DeMorgans Theoreme geben dieselbe Äquivalenz in „umgekehrter“ Form an. OR) mit invertierten Eingängen:

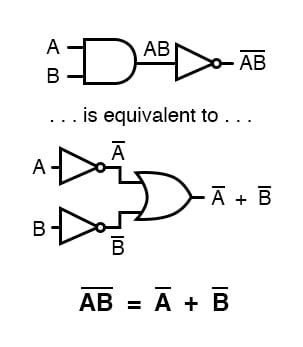
Ein langer Balken, der sich über den Begriff AB erstreckt, fungiert als Gruppierungssymbol und ist als solches völlig anders als das Produkt von A und B, das unabhängig invertiert ist.

Mit anderen Worten: (AB)‘ ist nicht gleich A’B‘. Da das „Primzahl“-Symbol (‚) nicht wie ein Balken über zwei Variablen gestreckt werden kann, sind wir gezwungen, Klammern zu verwenden, um es auf den gesamten Term AB im vorherigen Satz anzuwenden.

Ein Balken hingegen fungiert als eigenes Gruppierungssymbol, wenn er über mehr als eine Variable gestreckt wird.

Dies hat tiefgreifende Auswirkungen darauf, wie boolesche Ausdrücke ausgewertet und reduziert werden, wie wir noch sehen werden.

DeMorgan’s Theorem

DeMorgan’s Theorem kann man sich als das Brechen eines langen Balkensymbols vorstellen.

Wenn ein langer Balken gebrochen wird, ändert sich die Operation direkt unterhalb des Bruchs von Addition zu Multiplikation oder umgekehrt, und die gebrochenen Balkenstücke bleiben über den einzelnen Variablen. Zur Veranschaulichung:

Wenn mehrere „Schichten“ von Balken in einem Ausdruck vorhanden sind, kann immer nur ein Balken gebrochen werden, und es ist im Allgemeinen einfacher, die Vereinfachung zu beginnen, indem man den längsten (obersten) Balken zuerst bricht.

Zur Veranschaulichung nehmen wir den Ausdruck (A + (BC)‘)‘ und reduzieren ihn mithilfe der DeMorgan-Theoreme:

Dem Rat folgend, den längsten (obersten) Balken zuerst zu brechen, beginne ich damit, den Balken, der den gesamten Ausdruck umfasst, als ersten Schritt zu brechen:

Damit reduziert sich die ursprüngliche Schaltung auf ein UND-Gatter mit drei Eingängen, wobei der Eingang A invertiert ist:

Sie sollten nie mehr als einen Balken in einem Schritt brechen, wie hier gezeigt:

So verlockend es auch sein mag, Schritte zu sparen und mehr als einen Balken auf einmal zu brechen, führt es oft zu einem falschen Ergebnis, also tun Sie es nicht!

Es ist möglich, diesen Ausdruck richtig zu reduzieren, indem man den kurzen Balken zuerst bricht, anstatt den langen Balken zuerst zu brechen:

Das Endergebnis ist dasselbe, aber es sind mehr Schritte erforderlich als bei der ersten Methode, bei der der längste Balken zuerst gebrochen wurde.

Beachten Sie, dass wir im dritten Schritt den langen Balken an zwei Stellen gebrochen haben.

Das ist eine legitime mathematische Operation und nicht dasselbe wie das Brechen von zwei Balken in einem Schritt!

Das Verbot, mehr als einen Balken in einem Schritt zu brechen, ist kein Verbot, einen Balken an mehr als einer Stelle zu brechen.

Das Brechen an mehr als einer Stelle in einem Schritt ist in Ordnung; das Brechen von mehr als einem Balken in einem Schritt ist es nicht.

Sie werden sich vielleicht fragen, warum die Klammern um den Unterausdruck B‘ + C‘ gesetzt wurden, wenn man bedenkt, dass ich sie im nächsten Schritt einfach entfernt habe.

Ich habe dies getan, um einen wichtigen, aber leicht vernachlässigten Aspekt von DeMorgans Theorem zu betonen.

Da ein langer Balken als Gruppierungssymbol fungiert, müssen die Variablen, die zuvor durch einen unterbrochenen Balken gruppiert wurden, gruppiert bleiben, damit die richtige Rangfolge (Reihenfolge der Operation) nicht verloren geht.

In diesem Beispiel würde es wirklich nichts ausmachen, wenn ich nach dem Brechen des kurzen Balkens vergessen würde, Klammern zu setzen, aber in anderen Fällen könnte es sein.

Betrachten Sie dieses Beispiel, beginnend mit einem anderen Ausdruck:

Wie Sie sehen können, ist die Beibehaltung der Gruppierung, die durch die Komplementärbalken für diesen Ausdruck impliziert wird, entscheidend, um die richtige Antwort zu erhalten.

Lassen Sie uns die Prinzipien der DeMorgan’schen Theoreme auf die Vereinfachung einer Torschaltung anwenden:

Wie immer muss unser erster Schritt bei der Vereinfachung dieser Schaltung darin bestehen, einen äquivalenten booleschen Ausdruck zu erzeugen.

Wir können dies tun, indem wir am Ausgang jedes Gatters eine Beschriftung mit einem Unterausdruck anbringen, wenn die Eingänge bekannt werden. Hier ist der erste Schritt in diesem Prozess:

Als nächstes können wir die Ausgänge des ersten NOR-Gatters und des NAND-Gatters beschriften.

Bei Gattern mit invertiertem Ausgang finde ich es einfacher, einen Ausdruck für den Ausgang des Gatters ohne die endgültige Invertierung zu schreiben, mit einem Pfeil, der auf kurz vor der Invertierungsblase zeigt.

Dann schreibe ich an der Leitung, die aus dem Gatter herausführt (nach der Blase), den vollständigen, ergänzten Ausdruck.

Dies hilft sicherzustellen, dass ich keinen komplementären Balken im Unterausdruck vergesse, indem ich mich zwinge, die Aufgabe des Ausdrucksschreibens in zwei Schritte aufzuteilen:

Schließlich schreiben wir einen Ausdruck (oder ein Paar von Ausdrücken) für das letzte NOR-Gatter:

Nun reduzieren wir diesen Ausdruck mithilfe der Identitäten, Eigenschaften, Regeln und Theoreme (DeMorgan’s) der Booleschen Algebra:

Die äquivalente Gatterschaltung für diesen stark vereinfachten Ausdruck sieht wie folgt aus:

Rückblick:

• DeMorgan’s Theorem beschreibt die Äquivalenz zwischen Gattern mit invertierten Eingängen und Gattern mit invertierten Ausgängen. Einfach ausgedrückt ist ein NAND-Gatter äquivalent zu einem Negativ-ODER-Gatter und ein NOR-Gatter äquivalent zu einem Negativ-AND-Gatter.
• Wenn man in einem booleschen Ausdruck einen Komplementärbalken „bricht“, kehrt sich die Operation direkt unterhalb des Bruchs (Addition oder Multiplikation) um, und die gebrochenen Balkenstücke verbleiben über den jeweiligen Termen.
• Es ist oft einfacher, sich einem Problem zu nähern, indem man den längsten (obersten) Balken bricht, bevor man alle Balken darunter bricht. Versuchen Sie nie, zwei Balken in einem Schritt zu brechen!
• Komplementierungsbalken funktionieren als Gruppierungssymbole. Wenn also ein Balken gebrochen wird, müssen die darunter liegenden Begriffe gruppiert bleiben. Um diese gruppierten Begriffe können als Hilfe Klammern gesetzt werden, um eine Änderung der Rangfolge zu vermeiden.