Teoremas DeMorgan
Um matemático chamado DeMorgan desenvolveu um par de regras importantes relativas à complementação de grupos em álgebra Booleana.
Por complementação de grupo, refiro-me ao complemento de um grupo de termos, representado por uma barra longa sobre mais de uma variável.
Deve-se recordar do capítulo sobre portas lógicas que invertendo todas as entradas para uma porta inverte a função essencial dessa porta de AND para OR, ou vice-versa, e também inverte a saída.
Assim, uma porta OR com todas as entradas invertidas (uma porta NAND) comporta-se da mesma forma que uma porta NAND, e uma porta AND com todas as entradas invertidas (uma porta NAND) comporta-se da mesma forma que uma porta NOR.
Os teoremas de DeMorgan declaram a mesma equivalência na forma “para trás”: que inverter a saída de qualquer porta resulta na mesma função que o tipo oposto de porta (AND vs. OU) com entradas invertidas:
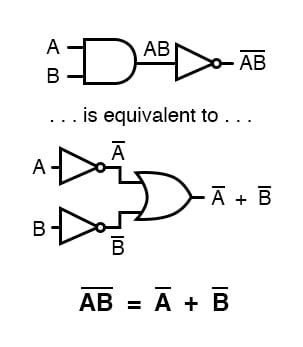
Uma barra longa que se estende sobre o termo AB actua como um símbolo de agrupamento, e como tal é totalmente diferente do produto de A e B independentemente invertido.
Por outras palavras, (AB)’ não é igual a A’B’. Porque o símbolo “prime” (‘) não pode ser esticado sobre duas variáveis como uma lata de barra, somos forçados a usar parênteses para que se aplique a todo o termo AB na frase anterior.
Uma barra, contudo, actua como o seu próprio símbolo de agrupamento quando esticado sobre mais do que uma variável.
Isto tem um impacto profundo na forma como as expressões booleanas são avaliadas e reduzidas, como veremos.
TeoremaDeMorgan
TeoremaDeMorgan pode ser pensado em termos de quebra de um símbolo de barra longa.
Quando uma barra longa é quebrada, a operação directamente por baixo da quebra muda de adição para multiplicação, ou vice-versa, e os pedaços de barra quebrados permanecem sobre as variáveis individuais. Para ilustrar:

Quando existem múltiplas “camadas” de barras numa expressão, só se pode quebrar uma barra de cada vez, e é geralmente mais fácil começar a simplificação quebrando primeiro a barra mais longa (mais alta).
Para ilustrar, vamos pegar na expressão (A + (BC)’)’ e reduzi-la usando os Teoremas de DeMorgan:

Segundo o conselho de quebrar primeiro a barra mais longa (mais alta), começarei por quebrar a barra cobrindo toda a expressão como um primeiro passo:

Como resultado, o circuito original é reduzido a três entradas E porta com a entrada A invertida:

Nunca se deve quebrar mais de uma barra num único passo, como ilustrado aqui:

Por mais tentador que seja conservar passos e quebrar mais de uma barra de cada vez, muitas vezes leva a um resultado incorrecto, por isso não o faça!
É possível reduzir adequadamente esta expressão quebrando primeiro a barra curta, em vez de quebrar primeiro a barra longa:

O resultado final é o mesmo, mas são necessários mais passos em comparação com a utilização do primeiro método, em que a barra mais longa foi quebrada primeiro.
Notem como no terceiro passo quebramos a barra longa em dois lugares.
Esta é uma operação matemática legítima, e não é o mesmo que partir duas barras num único passo!
A proibição de partir mais de uma barra num único passo não é uma proibição de partir uma barra em mais do que um lugar.
Partir em mais do que um lugar num único passo é bom; partir mais do que uma barra num único passo não é bom.
P>Vocês podem estar a perguntar-se por que razão foram colocados parênteses em torno da sub-expressão B’ + C’, considerando o facto de os ter acabado de remover no passo seguinte.
Fi-lo para enfatizar um aspecto importante mas facilmente negligenciado do teorema de DeMorgan.
Desde que uma barra longa funcione como um símbolo de agrupamento, as variáveis anteriormente agrupadas por uma barra quebrada devem permanecer agrupadas para que não se perca a devida precedência (ordem de funcionamento).
Neste exemplo, não importaria realmente se eu me esquecesse de colocar parênteses depois de quebrar a barra curta, mas em outros casos poderia.
Considere este exemplo, começando com uma expressão diferente:


Como pode ver, manter o agrupamento implícito pelas barras de complementação para esta expressão é crucial para obter a resposta correcta.
a>apliquem os princípios dos teoremas de DeMorgan à simplificação de um circuito de porta de comunicação:

Como sempre, o nosso primeiro passo na simplificação deste circuito deve ser gerar uma expressão booleana equivalente.
Podemos fazê-lo colocando uma etiqueta de subexpressão na saída de cada porta, à medida que as entradas se tornam conhecidas. Aqui está o primeiro passo neste processo:

P>Next, podemos etiquetar as saídas da primeira porta NOR e da porta NAND.
Ao lidar com portas de saída invertida, acho mais fácil escrever uma expressão para a saída da porta sem a inversão final, com uma seta apontando para imediatamente antes da bolha de inversão.
Então, no fio que sai do portão (após a bolha), escrevo a expressão completa e complementada.
Isto ajuda a garantir que não esqueço uma barra complementar na sub-expressão, obrigando-me a dividir a tarefa de escrita da expressão em dois passos:

Finalmente, escrevemos uma expressão (ou par de expressões) para a última porta NOR:

Agora, reduzimos esta expressão usando as identidades, propriedades, regras e teoremas (DeMorgan’s) da álgebra booleana:

O circuito de porta equivalente para esta expressão tão simplificada é o seguinte:

REVIEW:
- Os Teoremas do DeMorgan descrevem a equivalência entre portões com entradas invertidas e portões com saídas invertidas. Simplificando, um portão NAND é equivalente a um portão NOR negativo, e um portão NOR é equivalente a um portão NOR negativo.
- As barras de complementação funcionam como símbolos de agrupamento. Portanto, quando uma barra é quebrada, os termos por baixo dela devem permanecer agrupados. Os parênteses podem ser colocados em torno destes termos agrupados como uma ajuda para evitar a mudança de precedência.
>li> Quando se “quebra” uma barra de complementação numa expressão booleana, a operação directamente por baixo da quebra (adição ou multiplicação) inverte-se, e os pedaços de barra partidos permanecem nos respectivos termos.li> É muitas vezes mais fácil abordar um problema quebrando a barra mais longa (mais alta) antes de quebrar qualquer barra por baixo dela. Nunca se deve tentar quebrar duas barras num só passo!