Cuál es la diferencia entre PNP y NPN?

Este artículo apareció en Microwaves & RF y se ha publicado aquí con permiso.

Lo que aprenderá:

• El rendimiento máximo de un canal en función de la tasa de símbolos y el ancho de banda.
• El rendimiento máximo de un canal en función del ruido de interferencia.
• Cómo las consideraciones de rendimiento llegan hasta el usuario.

Es muy fácil y normal centrarse en las características principales de los componentes principales de un sistema o enlace de comunicaciones, y considerar otros elementos y cuestiones como periféricos y no tan importantes. El hecho de que esto haya sucedido de forma sorprendente con los enlaces de comunicaciones por satélite, especialmente los móviles remotos, es el motivo de esta misiva.

He aquí una situación hipotética. Usted es un soldado. Estás desplegado en una zona montañosa de Oriente Medio, llevas un terminal de satélite Intelsat antiguo para tener acceso inmediato de vuelta al cuartel general, y éste ha alquilado un transpondedor de 72 MHz para tu uso exclusivo.

Un lugar agradable y seguro es una cueva, por lo que se tiende un cable de comunicaciones a la terminal de satélite en la entrada de la cueva y te sientas a comprobar con tu estación de trabajo que está conectada a la terminal con un módem de modulación por desplazamiento de fase en cuadratura (QPSK). El control está bien, pero la comunicación es pésima. La compañía de satélites te garantiza 72 Mb/s (1 bit por Hz), pero apenas consigues menos de 35 Mb/s. ¿Deberías haber comprado un terminal más nuevo? ¿Debería usar otro sistema?

Tarifas de datos máximas de Nyquist

La respuesta real es lo que dijeron Harry Nyquist y Claude Shannon sobre las tasas de datos máximas en cada canal, incluyendo ese cable de comunicaciones. Harry Nyquist señaló, como se ha documentado exhaustivamente1, que el número máximo de bits que se pueden obtener a través de un canal (sin tener en cuenta el ruido) es:

Max R = 2 H Log2V

donde H es el ancho de banda del canal y V es el número de símbolos discretos (la codificación binaria por desplazamiento de fase, o BPSK, es 2, QPSK es 4, etc.).

Si no está familiarizado con el log2, no es difícil una vez que se acostumbra a él. El log2V es simplemente el exponente al que hay que elevar 2 para que sea igual a V. Así, si V es BPSK (2), entonces la expresión log2V es simplemente 1, ya que 21 es en realidad 2; y si V es QPSK (4), entonces la expresión log2V es 2 ya que 22 es en realidad 4, y así sucesivamente.

Si está utilizando un cable Cat 3 de 10 MHz, entonces la velocidad máxima de datos EN el terminal del satélite es BPSK 20 Mb/s, QPSK 40 Mb/s y 8PSK 30 Mb/s, en función de las relaciones log2. La figura 1 muestra el número de estados y su logaritmo en el equivalente de base 2. Por tanto, el límite de Nyquist, utilizando el módem QPSK, es de 40 Mb/s.

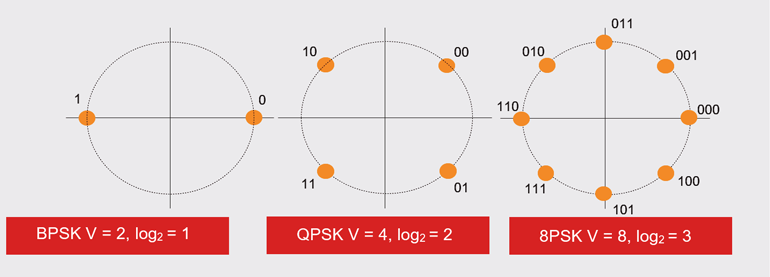1. BPSK, que tiene dos estados, tiene un valor log2 de 1; QPSK, que tiene cuatro estados, tiene un valor log2 de 2; y así sucesivamente.

Tarifas máximas de datos de Shannon

Bueno, Harry Nyquist estaba trabajando el tema de las tasas máximas de datos sin considerar el ruido mientras que Claude Shannon lo hacía estrictamente en función del ruido. Su ecuación2 dice:

Max R = H log2 (1 + SNR)

donde H es de nuevo el ancho de banda del canal y la SNR es la potencia de la señal dividida por la potencia del ruido, generalmente dada en dB. Supongamos que la SNR en ese mismo cable Cat 3 es de unos 30 dB o 1.000 en números brutos (la SNR debe reconvertirse a su valor racional para calcular una exponencial). Como hemos ido subiendo la escala de exponenciales de 2, podemos seguir haciéndolo. La figura 2 muestra esa progresión.

2. Un número, mostrado en la línea superior, tiene un valor exponencial, mostrado en la línea inferior, y demuestra la importancia de la temperatura de ruido del sistema en relación con el rendimiento de un canal.

Si redondeamos un poco para simplificar, 1.001 está más cerca de 1.024 que cualquier otro incremento y 2 elevado a la 10ª potencia te da un valor mucho más cercano que cualquier otro exponente. Sentado en su cueva con un cable Cat 3 de 10 MHz de ancho de banda, Claude Shannon dice que debería obtener una velocidad de datos de 10 x 106 (10) = 100 Mb/s.

Si Claude Shannon dice que puede obtener una velocidad de datos máxima en el terminal de comunicaciones por satélite de 100 Mb/s y Harry Nyquist dice que sólo puede obtener 40 Mb/s desde y hacia su estación de trabajo equipada con QPSK, ¿quién tiene razón?

Veamos otra analogía. La Universidad de Notre Dame tiene un equipo de fútbol con limitaciones académicas pero relativamente bueno. Por otro lado, tiene una gran banda de música porque los músicos más destacados suelen ser estudiantes de secundaria sobresalientes. Para entrar en el campo, la banda tiene que pasar por dos arcos, uno que permite 15 miembros en fila y otro que permite 10. ¿Cómo se forma la banda de música? Bueno, del mismo modo, Nyquist y Shannon no compiten. Sólo son dos puertas diferentes con dos limitaciones distintas.

No es sólo el sistema mayor. Son las idas y venidas hasta las manos que escriben en el teclado. Y los artículos originales publicados por el físico Nyquist3 y el matemático/ingeniero Shannon4 todavía tienen algo que decirnos.

1. Se puede encontrar un ejemplo de la ecuación en cualquier edición de Data and Computer Communications de William Stallings que aparece en el apartado Nyquist Bandwidth. Nota: Diferentes autores utilizan diferentes letras para designar la tasa de datos, el ancho de banda, etc.

2. Al igual que con Nyquist la ecuación se encuentra en cualquier edición de Data and Computer Communications de William Stallings, ésta aparece bajo la Fórmula de Capacidad de Shannon. Nota: Diferentes autores utilizan diferentes letras para designar la tasa de datos, el ancho de banda, etc.

3. Ciertos temas de la teoría de la transmisión telegráfica (que implicaban el límite) fueron presentados en la Convención de Invierno de la AIEE, Nueva York, N.Y., del 13 al 17 de febrero de 1928. Se volvió a publicar como «Classic Paper» en las Actas del IEEE en febrero de 2002.

4. «Communications in the Presence of Noise» se publicó en las Actas del IRE en enero de 1949, nueve años después de ser escrito.