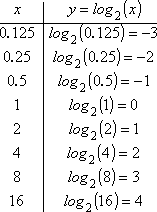Graficación de funciones logarítmicas: Introducción
Vuelve al índice de lecciones | Haz las lecciones en orden | Página para imprimir
Graficar funciones logarítmicas: Introducción (página 1 de 3)
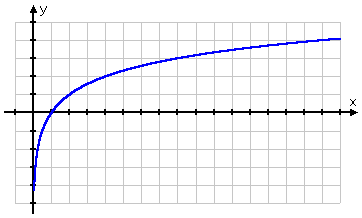
Por la naturaleza del logaritmo, la mayoría de las gráficas logarítmicas tienden a tener la misma forma, pareciéndose a una gráfica de raíz cuadrada:
| y = sqrt(x) | y = log2(x) |  |
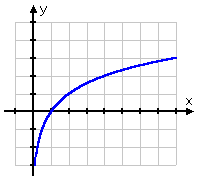 |
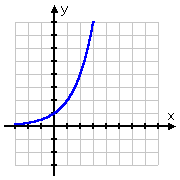
La gráfica de la raíz cuadrada comienza en el punto (0, 0) y luego se va hacia la derecha. Por otro lado, la gráfica del logaritmo pasa por (1, 0), desviándose hacia la derecha pero también deslizándose por el lado positivo del eje y. Recordando que los logaritmos son los inversos de las exponenciales, esta forma para la gráfica del logaritmo tiene mucho sentido: la gráfica del logaritmo, al ser la inversa de la exponencial, sería simplemente la «vuelta» de la gráfica de la exponencial:
| y = 2x | y = log2(x) |
 |
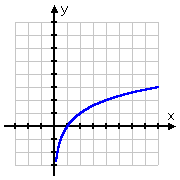 |
comparación de las dos gráficas, mostrando la línea de inversión en rojo |
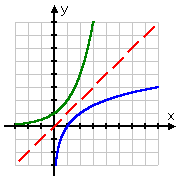 |
|
Es bastante sencillo graficar exponenciales. Por ejemplo, para graficar y = 2x, sólo tienes que introducir algunos valores de x, calcular los valores de y correspondientes y trazar los puntos. Pero, ¿cómo se grafican los logaritmos? Hay dos opciones. Aquí está la primera: Copyright © Elizabeth Stapel 2002-2011 Todos los derechos reservados
- Graficar y = log2(x).
- Dado que 21 = 2, entonces log2(2) = 1, y (2, 1) está en la gráfica.
- Como 3 no es una potencia de 2, entonces log2(3) será algún valor desordenado. Así que no me molestaré en graficar x = 3.
- Dado que 22 = 4, entonces log2(4) = 2, y (4, 2) está en la gráfica.
- Dado que 5, 6 y 7 tampoco son potencias de 2, me los saltaré y pasaré a x = 8.
- Dado que 23 = 8, entonces log2(8) = 3, por lo que (8, 3) está en la gráfica.
- La siguiente potencia de 2 es 16: como 24 = 16, entonces log2(16) = 4, y (16, 4) está en la gráfica.
- La siguiente potencia de 2, x = 32, es demasiado grande para mi gusto; no me apetece dibujar mi gráfico tan ancho, así que lo dejaré en x = 16.
Para graficar esto «a mano», primero necesito recordar que los logaritmos no están definidos para x negativo o para x = 0. Debido a esta restricción en el dominio (los valores de entrada) del logaritmo, ni siquiera me voy a molestar en encontrar los valores de y para, por ejemplo, x = -3 o x = 0. En su lugar, empezaré con x = 1, y trabajaré a partir de ahí, utilizando la definición del logaritmo.
Lo anterior me da el punto (1, 0) y algunos puntos a la derecha, pero ¿qué hago para los valores de x entre 0 y 1? Para este intervalo, necesito pensar en términos de potencias negativas y recíprocas. Al igual que la «mitad» izquierda de la función exponencial tenía pocos puntos graficables (el resto de ellos están demasiado cerca del eje x), también la «mitad» inferior de la función logarítmica tiene pocos puntos graficables, el resto de ellos están demasiado cerca del eje y. Pero puedo encontrar algunos:
Dado que 2-1 = 1/2 = 0,5, entonces log2(0,5) = -1, y (0,5, -1) está en la gráfica.
Dado que 2-2 = 1/4 = 0,25, entonces log2(0,25) = -2, y (0,25, -2) está en la gráfica.
Dado que 2-3 = 1/8 = 0,125, entonces log2(0.125) = -3, y (0,125, -3) está en la gráfica.
La siguiente potencia de 2 (a medida que x se mueve en esta dirección) es 1/16 = 2-4, pero el valor de x para el punto (0,0625, -4) parece demasiado pequeño para molestarse en él, así que lo dejaré con los puntos que ya he encontrado.
|
La lista de estos puntos me da mi gráfico T: |
|
Dibujando mis puntos y luego trazando la línea (¡recordando no ir a la izquierda del eje y!), obtengo este gráfico: |
|
Top | 1 | 2 | 3 | Volver al índice siguiente >>
|
Cite este artículo como: |
Stapel, Elizabeth. «Graficando funciones logarítmicas: Intro». Purplemath. Disponible en 2016
|