Jacobiano
Dado un conjunto 
de 
ecuaciones en 
variables 
, escritas explícitamente como
 |
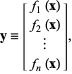(1)
|
o más explícitamente como
 |
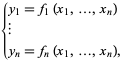(2)
|
La matriz jacobiana, a veces llamada simplemente «la jacobiana» (Simon y Blume 1994) se define por
 |
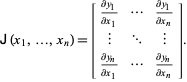(3)
|
El determinante de 
es el determinante jacobiano (confusamente, a menudo llamado también «el jacobiano») y se denota
 |
(4)
|
La matriz jacobiana y el determinante pueden calcularse en WolframLanguage utilizando
JacobianMatrix := Outer /; Equal @@ (Dimensions /@ {f, x}) JacobianDeterminant := Det] /; Equal @@ (Dimensions /@ {f, x})
Tomando la diferencial
 |
(5)
|
Demuestra que 
es el determinante de la matriz 
, y por lo tanto da los cocientes de los volúmenes (contenidos) de 
en 
y 
,
 |
(6)
|
Por tanto, aparece, por ejemplo, en el teorema del cambio de variables.
El concepto de jacobiano también puede aplicarse a 
funciones en más de 
variables. Por ejemplo, considerando 
y 
, los jacobianos
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
se puede definir (Kaplan 1984, p. 99).
Para el caso de 
variables, el jacobiano toma la forma especial
 |
(9)
|
donde 
es el producto punto y 
es el producto cruz, que puede expandirse para dar
 |
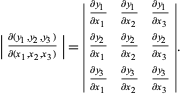(10)
|