¿Qué significa el factor de potencia?

Un factor de potencia bajo reduce la capacidad de distribución de un sistema eléctrico al aumentar el flujo de corriente. Por lo tanto, tener un factor de potencia bajo es ineficiente y caro. Pero, ¿qué es el factor de potencia y qué lo afecta?

Un sistema de distribución típico está limitado en la cantidad de corriente que puede transportar; el factor de potencia, expresado como un porcentaje, es un indicador de la cantidad de corriente total que puede utilizarse para crear trabajo (potencia activa). Cuanto más se acerque el factor de potencia a 1,00 (100%), menor será la cantidad de corriente necesaria para realizar dicho trabajo.

Por ejemplo, una carga con un factor de potencia de 0,80 significa que sólo el 80% de la potencia se utiliza efectivamente para realizar trabajo. En un mundo perfecto, toda la energía extraída del sistema eléctrico se convertiría en trabajo útil, pero esto no es así en el mundo real. Para describir completamente el factor de potencia, se necesitan complejas ecuaciones. Sin embargo, para una comprensión más sencilla, el Departamento de Energía de EE.UU. utiliza una analogía simple de la potencia necesaria para que un caballo tire de un carro por una vía.

En principio, el caballo se colocaría delante del vagón para proporcionar la fuerza de remolque más eficiente; sin embargo, eso no siempre es posible. El ángulo del remolque representa el cambio en el factor de potencia: cuanto más pequeño sea el ángulo, mejor será el factor de potencia; cuanto más grande sea el ángulo, menor será el factor de potencia (Figura 1).

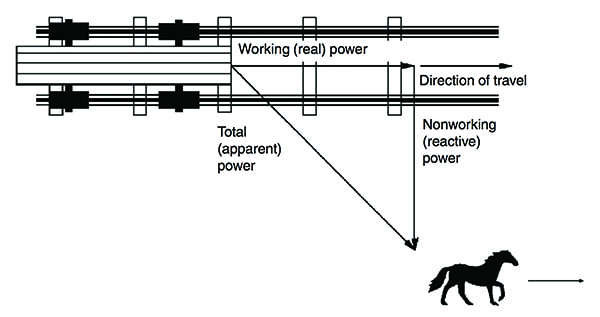
1. El ángulo afecta al trabajo útil. Los ángulos afectan al trabajo útil. La analogía mostrada aquí proporciona una visualización para ayudar a entender el factor de potencia. El factor de potencia se define como la relación entre la potencia real (de trabajo) y la potencia aparente (total). Si el caballo es conducido más cerca del centro de la pista, el ángulo de tracción lateral disminuye, y la potencia real se aproxima al valor de la potencia aparente. Fuente: Departamento de Energía de EE.UU.

La energía total necesaria para tirar del vagón es la potencia aparente. La energía real que mueve el vagón es la potencia real. La energía no utilizada por el ángulo de tracción del caballo es la potencia reactiva. En otras palabras, la potencia real, también denominada potencia de trabajo (kW), realiza el trabajo real de movimiento, calor y luz. La potencia reactiva, o potencia que no funciona (kVar), sostiene el campo magnético de una carga reactiva (normalmente inductiva). La corriente utilizada para crear la potencia reactiva no se utiliza para crear trabajo; sin embargo, esta corriente supone una carga para el sistema de distribución, el proveedor eléctrico y la factura eléctrica de una instalación.

La suma vectorial de la potencia de trabajo y la potencia no de trabajo es la potencia total (potencia aparente):

Potencia aparente = √ (Potencia real2 + Potencia reactiva2)

que se utiliza para calcular el factor de potencia:

Factor de potencia = Potencia real / Potencia aparente = coseno del ángulo (ϕ)

Fundamentos de la tensión y la corriente

Para entender el factor de potencia, primero debemos comprender algo de teoría básica de la corriente alterna (CA) y las formas de onda asociadas a ella. La tensión en un sistema de CA alterna entre positivo y negativo (en forma sinusoidal) y obliga a la corriente a comportarse de forma similar. Esto ocurre 60 veces por segundo (en un sistema de 60 Hz), y va de 0 a 360 grados. A diferencia de los sistemas de CA, la tensión en un sistema de corriente continua (CC) constante no cambia.

Debido a que el valor instantáneo de la tensión de CA cambia continuamente, la ciencia ha definido una medida diferente para las cantidades de CA, a saber, el valor RMS (raíz cuadrada media). El valor RMS de una forma de onda de CA produce el mismo efecto de calentamiento que una forma de onda de CC del mismo valor.

El RMS es la raíz cuadrada de la media aritmética de los cuadrados de un conjunto de los valores instantáneos a lo largo de un período (ciclo). Cuando la tensión y la corriente son puramente sinusoidales, la tensión y la corriente RMS pueden hallarse a partir de la tensión y la corriente de pico (pk):

VRMS = Vpk / √2

119.5 VRMS = 169 Vpk / 1,414

De forma similar,

IRMS = Ipk / √2

75 ARMS = 106 Apk / 1,414

Se estará preguntando, ¿qué tiene que ver esto con el factor de potencia? Los cálculos de potencia para CA requieren el conocimiento de la tensión RMS, la corriente RMS y la relación de fase sinusoidal. Así que, para resumir, RMS es una medida del efecto de calentamiento, calculada a partir de una forma de onda, que permite comparar la CA con la CC. Cualquier cambio de fase de una forma de onda sinusoidal pura indica el factor de potencia.

A continuación se muestra una comparación de cómo el factor de potencia afecta a los kVA de salida en dos cargas monofásicas diferentes.

Para un calentador eléctrico de 9 kW (120 VAC, 75 A) con un factor de potencia (PF) de entrada de 1,0:

P = √1ϕ x 120 VAC x 75 A x 1,0 PF = 9 kW

kVA = √1ϕ x 120 VAC x 75 A = 9 kVA

Para un cargador de baterías de 9 kW (120 VAC, 75 A) con 0.866 PF de entrada:

P = √1ϕ x 120 VAC x 86,6 A x 0,866 PF = 9 kW

kVA = √1ϕ x 120 VAC x 86,6 A = 10,392 kVA

Aunque cada carga consume 9 kW de potencia, el factor de potencia de entrada del cargador de baterías es de 0,866. El factor de potencia más bajo requiere 11,6 A adicionales para funcionar, que finalmente proporciona la compañía eléctrica. No sólo hay que comprar la corriente reactiva adicional, sino que también hay que aumentar el tamaño del sistema de distribución para manejar la corriente adicional.

¿Qué afecta al factor de potencia?

El factor de potencia se refiere a la relación entre la potencia activa (útil) y la potencia aparente (total). Esta relación es una medida de la eficacia con la que se utiliza la electricidad.

Cargas resistivas lineales. En un sistema de CA, las cargas se clasifican por la forma en que toman la corriente. Una carga resistiva lineal es una carga puramente resistiva sin componentes inductivos ni capacitivos, como los calentadores eléctricos y la iluminación incandescente. Las curvas de tensión y corriente interseccionan la coordenada cero en el mismo punto.

La curva de potencia (P) de la figura 2 se calcula mediante la tensión (V) y la corriente (I), que se muestra como el área positiva del gráfico. En este ejemplo, la tensión y la corriente son 120 VRMS y 75 ARMS, respectivamente. El producto de ambos es 9 kVA o 9 kW. La tensión y la corriente están «en fase», y el 100% de la potencia (potencia de trabajo) se utiliza efectivamente para realizar un trabajo útil. El factor de potencia para este tipo de carga es de 1,0.

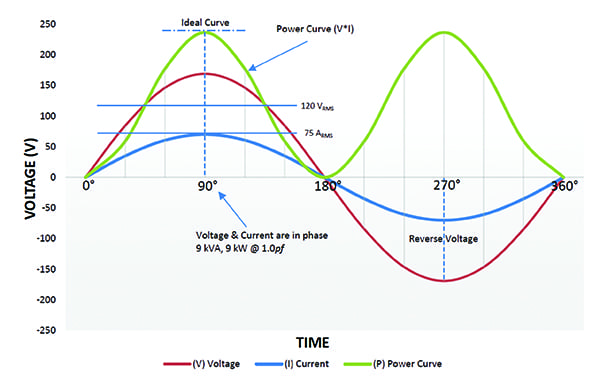
2. Cargas resistivas lineales. Cargas resistivas lineales. La tensión y la corriente están en fase con un factor de potencia igual a 1,0 para cargas puramente resistivas. Cortesía: Ametek Solidstate Controls

Cargas lineales no resistivas/reactivas. No es habitual encontrar cargas puramente resistivas; la mayoría de las cargas tienen un componente reactivo adicional. Estas cargas no resistivas/reactivas constituyen un gran porcentaje de todas las cargas. La forma de onda de la corriente se desplaza de la forma de onda de la tensión para que esté «desfasada». Si la carga es inductiva, la corriente va por detrás de la tensión; si la carga es capacitiva, la corriente va por delante.

Las instalaciones industriales suelen tener cargas con factor de potencia retardado (cargas inductivas). Este tipo de cargas pueden ser motores de inducción, reactancias y transformadores. Las cargas con factor de potencia líder (cargas capacitivas) son menos comunes y suelen ser cables subterráneos o ciertas fuentes de alimentación conmutadas.

En la Figura 3, la misma carga de la Figura 2 tiene ahora la forma de onda de tensión y corriente desfasada 30 grados. Dado que se trata de una forma de onda inductiva, la corriente está ahora retrasada.

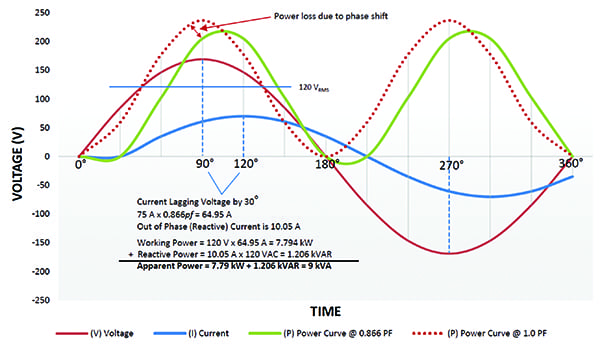
3. Cargas inductivas. La tensión y la corriente están desfasadas para las cargas lineales no resistivas/reactivas. En este ejemplo de carga inductiva, la corriente va 30 grados por detrás de la tensión con un factor de potencia de 0,866. Cortesía: Ametek Solidstate Controls

Cargas no lineales-armónicas. Los entornos industriales de hoy en día no sólo tienen cargas resistivas, inductivas y capacitivas, sino que muchos también incluyen equipos basados en el estado sólido, como fuentes de alimentación conmutadas, accionamientos de CC, accionamientos de frecuencia variable (VFD), balastos electrónicos, soldadores de arco y hornos con control de temperatura. Todas ellas son cargas no lineales, o cargas en las que la corriente no es sinusoidal, aunque la tensión sea sinusoidal. La naturaleza no sinusoidal de estas formas de onda se expresa mediante armónicos.

Los armónicos son formas de onda de amplitud variable a frecuencias que son múltiplos de la frecuencia fundamental de la tensión (50 Hz o 60 Hz). Se superponen a la forma de onda sinusoidal de la corriente para crear la forma de onda total de la corriente. La figura 4 es un ejemplo de dicha forma de onda de la corriente.

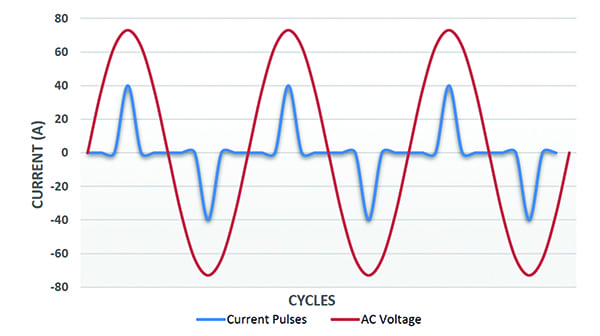
4. Cargas no lineales. Este gráfico muestra las formas de onda de tensión y corriente de una fuente de alimentación no lineal con armónicos. Se muestra sin un desplazamiento de fase de la corriente de 30 grados para mayor claridad. Cortesía: Ametek Solidstate Controls

El valor RMS de toda la corriente se encuentra sumando el valor RMS de cada corriente armónica. Dada una forma de onda de 60 Hz, esto significa que la segunda frecuencia armónica sería de 120 Hz (60 Hz x 2 = 120 Hz) y las frecuencias armónicas tercera, cuarta y quinta serían de 180 Hz, 240 Hz y 300 Hz, respectivamente. Como múltiplos de la frecuencia fundamental, los armónicos pueden expresarse como 2f, 3f, 4f, etc.

La distorsión armónica total (THD) de la corriente es la suma de todos los componentes armónicos de la forma de onda de la corriente comparados contra el componente fundamental de la onda de la corriente. Como se muestra a continuación, es una relación entre el valor RMS de los armónicos de la corriente y el valor RMS de la corriente fundamental.

DTH = RMS de los armónicos de la corriente / RMS de la corriente fundamental = √(I22 + I32 + I42 + …) / I1 x 100%

Para formas de onda puramente sinusoidales, el desplazamiento de fase entre la tensión y la corriente es suficiente para cuantificar el factor de potencia (FP). Para las formas de onda que no son sinusoidales, se utiliza el término factor de potencia de desplazamiento (DpPF) para cuantificar el desplazamiento de fase entre las fundamentales de las dos formas de onda (los componentes de 50-Hz o 60-Hz). Para las mismas formas de onda no sinusoidales, se define un término para cuantificar el efecto de los armónicos sobre el FP. Este término se denomina factor de potencia de distorsión (DF).

DF = 1 / √(1 + THD2)

Para hallar el factor de potencia total (FP), se utiliza la siguiente ecuación:

PFT = DF x DpPF

Correlaciones del factor de potencia

Para cargas lineales, el triángulo de potencia es un triángulo rectángulo que muestra las relaciones entre la potencia de trabajo, la reactiva y la aparente. La relación entre la potencia de trabajo y la aparente es el FP. El valor puede oscilar entre 0,0 y 1,0.

La potencia de trabajo, también llamada potencia verdadera, potencia real o potencia activa, realiza el trabajo real de movimiento/calefacción/iluminación, etc. y se mide en vatios (W). La potencia reactiva mantiene el campo magnético o eléctrico en dispositivos como las bobinas de los solenoides, los devanados de los motores, los devanados de los transformadores, los condensadores y los balastos, sin realizar un trabajo real. Esta energía extra se mide en voltios-amperios reactivos (VAR) y a veces se denomina potencia «sin vatios». La potencia aparente combina la potencia de trabajo y la potencia reactiva, y se mide en voltios-amperios (VA).

El ángulo de fase (ϕ) en grados, representa la «ineficiencia» de la carga y corresponde a la impedancia reactiva total (Z) al flujo de corriente en la carga. Cuanto mayor sea el ángulo de fase, mayor será la potencia reactiva. Las cargas no lineales añaden un elemento extra a la potencia total (aparente) sin añadir a la potencia activa, disminuyendo aún más el factor de potencia. ■

-David McKinnon es ingeniero de aplicaciones senior de Ametek Solidstate Controls. Un agradecimiento especial a Bogdan Proca, PhD y Doug King por sus contribuciones.